Прежде чем приступить к обсуждению механизмов преобразования изображения, дадим определение условий фиксации положения, дающих возможность показать соотношения между объектами (элементами) до и после выполнения преобразований.
Система правил, соотношений и изобразительных (графических) средств, позволяющая задать (определить) положение объекта внимания на плоскости или в пространстве, определяется как система отсчета, система координат (КС), по которой каждой точке пространства ставится в соответствие набор чисел (координат ). Число координат, которые требуются для описания положения точки, определяет размерность пространства и соответственно наличие двухмерной и трехмерной графики. Двухмерная графика использует два понятия – высота и ширина и не вызывает особых затруднений при работе с изображением. В понятии трехмерная графика заложено указание на то, что придется работать с тремя пространственными измерениями – высотой, шириной и глубиной. Не вдаваясь в тонкости понятия “трехмерная графика”, отметим, что при работе с графическими средствами компьютерной графики необходимо помнить - созданные изображения реальных объектов существуют только в памяти компьютера. Они не имеют физической формы, поскольку это не что иное, как совокупность математических уравнений и движение электронов в микросхемах. А так как эти объекты не могут существовать вне компьютера, то единственным способом их увидеть в реальном свете, является добавление новых уравнений, описывающих условия освещения и точки зрения.
Основным отличием двухмерной графики от трехмерной является полное отсутствие у двухмерных объектов (изображений) третьей координаты – глубины, величины, характеризующей пространственные свойства объекта. Рисунки на плоскости характеризуются только шириной и высотой. И если ваше изображение таково, что создает иллюзию наличия третьей компоненты, то любая попытка взглянуть на объект с иного ракурса всегда будет связана с необходимостью перерисовывания объекта заново.
Если при моделировании трехмерные объекты приобретают координату глубины, то однажды нарисовав такие объекты, потом имеется возможность рассматривать их под любым углом зрения, не перерисовывая.
Положение каждой точки в пространстве определяется тройкой чисел – координатами (шириной, высотой и глубиной). Таким образом, через каждую точку можно провести три координатные оси виртуального пространства. Координатная ось – это воображаемая линия пространства, определяющая направление изменения координаты. Точка пересечения трех осей, имеющая координаты (0,0,0) – это точка начала координат.
В машинной графике в зависимости от характера решаемых задач, от структуры представления изображений и от процесса обработки графических данных, используются различные координаты:
полярные, цилиндрические, сферические;
относительные;
пользователя;
физические;
нормализованные;
однородные.
Мировой координатой называют независимую от устройства декартову координату, используемую в прикладной программе при задании графических входных и выходных данных. Будем говорить, что на плоскости задана декартова прямоугольная система координат, если определена пара взаимно перпендикулярных осей и при этом обусловлено какая из этих осей является осью ординат, какая - осью абсцисс, а также единичный (масштабный) отрезок по осям. На рис. 3.14 изображена декартова система координат и определенная на ней точка M. Опустим из точки M перпендикуляры на оси OX и OY . Точки пересечения этих перпендикуляров с осями координат обозначены соответственно L и K . Абсциссой точки M называется отрезок оси OX, а ординатой – величина отрезка оси Y. Пару чисел x и y, где x= , y= называют координатами точки M в выбранной системе координат. Тот факт, что точка M имеет координаты x и y записывается так: M(x,y). При этом сначала пишется абсцисса, а затем ордината точки M .
Таким образом, каждой точке M плоскости соответствует пара действительных чисел (x,y ) – координаты этой точки. Наоборот, каждой паре действительных чисел (x,y ) соответствует, и при том только одна, точка M плоскости, для которой эти числа будут ее координатами.
Следовательно, введение на плоскости декартовой прямоугольной системы координат позволяет установить взаимно однозначное соответствие между множеством точек на плоскости и множеством пар действительных чисел на плоскости. Это соответствие дает возможность сводить изучение множеств точек на плоскости к изучению множеств пар действительных чисел, то есть, применять к изучению вопросов геометрии алгебраические методы. Это же соответствие дает возможность давать геометрическую интерпретацию некоторым вопросам алгебры и других дисциплин.
Рассматривая прикладной аспект КС, необходимо отметить следующее. Поскольку координаты по своей природе являются безразмерными, позиционирование объектов выполняется в единицах, которые являются естественными для данного приложения и пользователя. Например, требуется показать график помесячного выхода продукции в течение года. Координаты в этой КС (x – месяц; y – выход продукции) называются координатами пользователя , а поскольку они позволяют задавать объекты в двухмерном и трехмерном мире их также называют глобальными координатами.
Если в рассматриваемом векторном пространстве не предполагается возможным сравнение длин единичных векторов (орт), |e 1 |, |e 2 |, |e 3 |, то такое пространство называется аффинным . Аффинное векторное пространство позволяет изучать общие свойства фигур, изменяющиеся при произвольном преобразовании системы координат. Аффинная и декартова системы координат на плоскости устанавливают взаимно однозначное соответствие между точками и координатами.
Аффинная или декартова система координат называется правой, если совмещение положительной полуоси х с положительной полуосью у осуществляется поворотом оси Ox в направлении, противоположном направлению движения часовой стрелки на угол, меньший p. В противном случае система координат называется левой.
Если отрезки равны (случай метрического векторного пространства), а угол между осями ¹90 0 КС называется косоугольной . То есть кроме декартовой КС существуют и другие системы координат, позволяющие определить положение точки на плоскости (пространстве) с помощью пар (троек) действительных чисел. К таким КС относится, например, полярная система координат.
Полярная система координат. Определим на плоскости точку O и проходящую через нее ось OP. Точка O назовем полюсом, а полуось (луч), выходящую из точки O в положительном направлении, - полярной осью . Задание полюса полярной оси OP и единичного (масштабного) отрезка OE определяет на плоскости полярную систему координат. Полярным радиусом r любой точки M называется длина отрезка . Полярным углом j точки M называется угол наклона направленного отрезка к полярной оси OP . Угол j определяется с учетом знака и с точностью до слагаемого вида 2kp , гдe k – целое число.
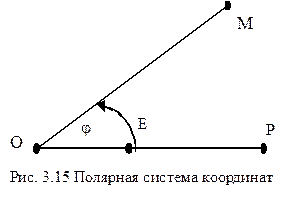Числа r
и j
, полярный радиус и полярный угол точки M,
называются полярными координатами.
Точка с полярными координатами обозначается так: M(r,j
) или (r,j
) .
Таким образом, задание любой пары действительных чисел (r,j ), ³ 0 позволяет построить на плоскости одну точку M , для которой эти числа являются ее полярными координатами.
При создании изображений достаточно часто приходится пользоваться одновременно декартовыми прямоугольными и полярными координатами точек. Практический интерес представляют формулы, позволяющие по декартовым координатам рассчитывать полярные координаты и наоборот.
Пусть точка M произвольная точка плоскости, x и y – ее декартовы координаты, r,j - полярные. Так как
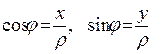
Формулы (1) выражают прямоугольные декартовы координаты точки M через полярные координаты.
то есть, , следовательно
Формулы (2) позволяют определить полярные координаты точки M по ее декартовым координатам. Если точка M не лежит на оси OY, то из формул (2) следует соотношение
Физической координатой считают координату, заданную в системе координат, которая зависит от устройства.
Нормализованной координатой называют координату, заданную в промежуточной, независимой от устройств, системе координат и нормированную относительно некоторого диапазона, обычно от 0 до 1. При этом изображение, выраженное в нормализованных координатах, располагается в одной и той же относительной позиции при визуализации на любое устройство. Нормализованные координаты используются в случае, если область трехмерного пространства, ограниченная кубом, со стороной h отображается в ту же область, ограниченную кубом со стороной b", при этом используется нормирующий множитель, делением на который получают нормализованные координаты. Координаты мировой системы иногда приводятся к нормализованному виду.
Приборная система координат всегда нормирована. Координаты обычно задаются в десятичных долях в диапазоне от О до 1 или в целых единицах, например, растра экрана дисплея (размер 1024 X 10*4 единиц растра).
Однородная система координат широко применяеся в машинной графике и позволяет n-мерный объект представить в (n +1) - мерном пространстве, путем добавления еще одной координаты - скалярного множителя. Однородные координаты являются основными в проективной геометрии, в машинной графике они удобный искусственный прием, позволяющий линеанизировать перспективные изображения. Однородные координаты дают возможность записывать несобственные (бесконечно удаленные) точки пространства, а также выражать аффинные преобразования в удобной матричной форме, избегая переполнения разрядной сетки ЭВМ за счет нормализации чисел.
Определяются однородные координаты следующим образом. Пусть на плоскости заданы система аффинных координат и произвольная точка Р с координатами (х, у). Введем в рассмотрение систему координат, в которой для описания вектора положения точки вводится третья компонента. Назовем однородной системой координат любую тройку одновременно не равных нулю чисел а 1 , а 2 , а 3 , связанных соотношением
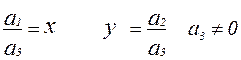
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке M(x, y) на плоскости ставится в соответствие точка M’(x, y) в пространстве. Заметим, что произвольная точка на прямой, соединяющей начало координат 0(0, 0, 0) с точкой М(x, y, 1), может быть задана тройкой чисел hx, hy, h (hx, hy, h ) при h¹0. Вектор, определяемый тройкой чисел hx, hy, h , является направляющим вектором прямой, соединяющим точки 0 и M’. Эта прямая пересекает плоскость Z=h в точке (x, y, h ), которая однозначно определяет точку x, y координатной плоскости XOY . То есть, между точкой x, y и множеством точек (hx, hy, h) h¹0 устанавливается
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. И, решая ту или иную геометрическую и физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой данная
задача решается проще, удобнее. Рассмотрим некоторые координатные системы, отличные от прямоугольных.
20.1. Косоугольные (аффинные) координаты.
На плоскости они определяются так.
Проведем на плоскости через данную точку О две произвольные прямые и введем на каждой из них координату, отсчитанную от точки О (масштабные отрезки на осях могут быть различной длины, рис. 20.1). Обозначим эти координаты XJ и прямые назовем осями , т. е. так же, как в случае прямоугольных координат, но только оси теперь не предполагаются взаимно перпендикулярными.
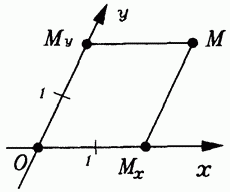
Любой точке М плоскости сопоставляем на оси точку в которой эту ось пересекает прямая, параллельная оси у. Аналогично определяем точку на оси у. Косоугольными координатами точки М называются координаты точек на осях х и у.
В пространстве косоугольные координаты вводятся так. Проведем через данную точку О три произвольные прямые, не лежащие в одной плоскости, и введем на каждой из них координату, отсчитываемую от точки О. Обозначим эти координаты через x,y,z, а прямые назовем осями
Любой точке М пространства соответствует на оси точка в которой эту ось пересекает плоскость, проходящая через точку М, параллельно плоскости а если М лежит в плоскости , то полагаем Аналогично определяем на осях у и z точки . За координаты х, у, z точки М принимаются координаты точек на соответствующих осях (рис. 20.2). Если оси взаимно перпендикулярны, то косоугольные координаты становятся прямоугольными.
1. Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X "X и Y "Y O , которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y "Y вверх, ось X "X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X "X и Y "Y , называются координатными углами или квадрантами (см. рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y . Координата x равна длине отрезка OB , координата y - длине отрезка OC в выбранных единицах измерения . Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y "Y и X "X соответственно. Координата x называется абсциссой точки A , координата y - ординатой точки A . Записывают так: А (x , y )
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату.
2. Полярные координаты.
Полярная сетка, на которой отложено несколько углов с пометками в градусах.
Полярная система координат - двумерная система координат, в которой каждая точка на плоскости определяется двумя числами - углом и расстоянием. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде расстояний и углов; в более распространенной, декартовой или прямоугольной системе координат, такие отношения можно установить только путем применения тригонометрических уравнений.
Полярная система координат задается лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается φ, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.
Определенная таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
3. Деление отрезков в данном отношении.
Требуется разделить отрезок АВ, соединяющий точки A(x1;y1) и В(х2;y2) в заданном отношении λ > 0, т. е..jpg" align="left" width="84 height=84" height="84">
Решение : Введем в рассмотрение векторы http://pandia.ru/text/78/214/images/image006_41.gif" width="18" height="13 src=">..gif" width="79" height="15 src=">, т. е. и т. е..
Уравнение (9.1) принимает вид
Учитывая, что равные векторы имеют равные координаты, получаем:
http://pandia.ru/text/78/214/images/image014_27.gif" width="56 height=28" height="28"> (9.2) и
http://pandia.ru/text/78/214/images/image016_26.gif" width="60 height=29" height="29"> (9.3)
Формулы (9.2) и (9.3) называются формулами деления отрезка в данном отношении . В частности, при λ = 1, т. е..gif" width="54" height="29 src=">. В этом случае точка М(х;у) является серединой отрезка АВ.
Замечание:
Если λ = 0, то это означает, что точки A и Μ совпадают, если λ < 0, то точка Μ лежит вне отрезка АВ - говорят, что точка M делит отрезок АВ внешним образом , т. к. в противном случае , т. е. AM + MB = 0, т. е. АВ = 0).
4. Расстояние между точками.
Требуется найти расстояние d между точками A(x1;y1) и В(х2;y2) плоскости .
Решение
: Искомое расстояние d равно длине вектора , т. е. 
5. Уравнение прямой, проходящей через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) иM2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
Кроме того, для точки М1 можно записать:
Решая совместно эти уравнения, получим:
.
Это уравнение прямой, проходящей через две точки в пространстве.
6. Определители 2-го порядка.
Значение определителя 2-го порядка легко вычисляется по определению используя формулу.
7. Определители 3-го порядка.
http://pandia.ru/text/78/214/images/image030_15.gif" width="120" height="61 src="> схема вычисления определителя методом треугольника, т. о.:
http://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="183" height="73 src=">
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
http://pandia.ru/text/78/214/images/image039_14.gif" width="79" height="46">.gif" width="264" height="48">.gif" width="120" height="29">.gif" width="110" height="46 src=">
Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов
Найдем произведение
http://pandia.ru/text/78/214/images/image049_13.gif" width="108" height="41"> или короче A ∙X=B .
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т. к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .
Пусть определитель матрицы отличен от нуля |A
| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1
, обратную матрице A
: http://pandia.ru/text/78/214/images/image051_13.gif" width="168" height="59">
Решить матричным способом следующую систему уравнений:
Внимание: Нули появляются, если нет одной переменной, т. е., например, если Х3 не дан в условии, то он автоматически равен нулю. Так же и с Х1 и Х2
http://pandia.ru/text/78/214/images/image057_9.gif" width="56 height=54" height="54">
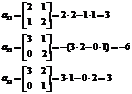
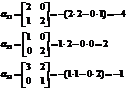
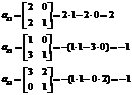
http://pandia.ru/text/78/214/images/image065_8.gif" width="160 height=51" height="51">
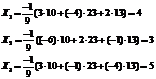Ответ:
# а) Дано:
http://pandia.ru/text/78/214/images/image074_5.gif" width="59 height=16" height="16">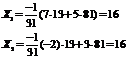
Ответ:
http://pandia.ru/text/78/214/images/image081_5.gif" width="106" height="50 src=">
Найдем обратную матрицу.
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
http://pandia.ru/text/78/214/images/image083_4.gif" width="172" height="52 src=">
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
http://pandia.ru/text/78/214/images/image085_5.gif" width="187" height="53 src=">
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1. Квадратная матрица, получившаяся правее единичной и есть обратная к главной.
http://pandia.ru/text/78/214/images/image087_4.gif" width="172" height="52 src=">
11. Векторы. Сложение векторов.
http://www. bigpi. *****/encicl/articles/15/1001553/1001553A. htm
Вектором называют величину, характеризуемую числовым значением, направлением в пространстве и складывающейся с другой, себе подобной величиной геометрически .
Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как http://pandia.ru/text/78/214/images/image089_5.gif" width="17" height="17 src=">.jpg" alt="сложение векторов a+b=b+a, a+(b+c)=(a+b)+c" width="110" height="46">
Теорема : Каковы бы ни были три точки A, B и C, имеет место векторное равенство http://pandia.ru/text/78/214/images/image094_4.gif" width="126" height="49">
При сложении двух векторов часто используют так называемое «правило параллелограмма ». При этом строят параллелограмм, используя слагаемые векторы в качестве его смежных сторон. Диагональ параллелограмма, проведённая из точки, где соединяются начала векторов, и является искомой суммой (рис. 4, слева).
Легко видеть (рис. 4, справа), что это правило приводит к тому же результату, что и указанный выше способ. При сложении более двух векторов «правило параллелограмма
» практически не используется из-за громоздкости построений. Сложение векторов коммутативно, то есть,
а
+ b
= b
+ а
.
И еще, сумма определенного числа векторов не зависит от порядка, в котором они складываются, то есть, (а + b ) + d = a + (b + d ). В этом случае говорят, что сложение векторов ассоциативно, то есть для него выполняется сочетательный закон.
12. Скалярное произведение векторов.
http://www. dpva. info/Guide/GuideMathematics/linearAlgebra/ScalarVectorsMultiplication/
Скалярное произведение векторов - это операция над двумя векторами, результатом которой является число (не вектор).
http://pandia.ru/text/78/214/images/image097_5.gif" width="86" height="23">
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними. Необходимо заметить, что угол между двумя векторами - это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.
Непосредственно из определения следуют следующие простейшие свойства:
1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор - нулевой.
2. Скалярное произведение любых перпендикулярных векторов a и b равно нулю.
3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них - нулевой.
4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.
5. Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.
Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.
(Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто :
Пусть есть вектор AB, А - начало вектора, В - конец, и координаты этих точек
А=(a1,a2,a3), В=(b1,b2,b3)
Тогда координаты вектора АВ:
АВ={b1-a1, b2-a2, b3-a3}.
Аналогично в двухмерном пространстве - просто отсутствуют третьи координаты)
Итак, пусть даны два вектора, заданные набором своих координат:
а) В двухмерном пространстве(на плоскости) ..gif" width="49" height="19 src=">
Тогда их скалярное произведение можно вычислить по формуле:
б) В трехмерном пространстве: ;
Аналогично двухмерному случаю, их скалярное произведение вычисляется по формуле:
http://pandia.ru/text/78/214/images/image103_3.gif" width="78" height="23 src=">.gif" width="98" height="24 src=">
Аналогично вычисляется длина вектора b.
Значит, 
, 
Искомый угол найден.
13. Векторное произведение.
http://www. dpva. info/Guide/GuideMathematics/linearAlgebra/vectorVectorsMultiplication/
Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами:
http://pandia.ru/text/78/214/images/image111_3.gif" width="83" height="27">, где a и b .
3) Вектор направлен таким образом, что если привести вектора http://pandia.ru/text/78/214/images/image117_3.gif" width="13" height="24 src=">.gif" width="13" height="24"> до вектора будет ПРОТИВ часовой стрелки.
Для большей ясности приведем пример - на рисунке справа вектор - векторное произведение векторов а и b. Как сказано в определении, мы привели все три вектора к общему началу, и тогда, если смотреть на вектора a и b с конца вектора , кратчайший поворот от вектора а до вектора b будет против часовой стрелки.
http://pandia.ru/text/78/214/images/image119_3.gif" width="76" height="25">
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее: 
det A http://pandia.ru/text/78/214/images/image182_2.gif" width="56 height=32" height="32">
7.2 Нахождение Определителя Матрицы 3-го порядка по правилу треугольника
http://pandia.ru/text/78/214/images/image186_2.gif" width="132" height="45">
Каждому элементу квадратной Матрицы (порядок которых больше, или равен трем), можно поставить в соответствие два числа, называемые МИНОРОМ или АЛГЕБРАИЧЕСКИМ ДОПОЛНЕНИЕМ. Минором элемента Aij квадратной Матрицы А (любого порядка) называется ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ, получаемый из Матрицы А методом вычеркивания строки и столбца, на пересечении которых стоит элемент Aij. Знак M - обозначение Минора.
http://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="35" height="19">
http://pandia.ru/text/78/214/images/image194_1.gif" width="96 height=82" height="82">
ЭЛЕМЕНТЫ | Минор | Алгебраическое Дополнение |
||||||||||||||||
Пусть А = некоторая Матрица III-го порядка, тогда определитель матрицы А равен:
Замечание: Определитель можно вычислить по элементам любой строки или любого столбца данной Матрицы.
# Найти определитель Матрицы по элементам первой строки и первого столбца:
http://pandia.ru/text/78/214/images/image201_0.gif" width="58" height="56 src=">
http://pandia.ru/text/78/214/images/image203_0.gif" width="253" height="34 src=">
7.3 ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ n-го порядка
Пусть А - квадратная Матрица n-го порядка. Тогда, Определитель Матрицы n-го порядка будет выглядеть так:
Разложив по элементам 1 строки найти элементы Матрицы А
http://pandia.ru/text/78/214/images/image206_0.gif" width="38" height="55">
6. Если в какой-то строке или столбце определителя прибавить соответственно элементы другой строки или столбца, умноженные на одно и то же число, то определитель не изменит своей величины.
http://pandia.ru/text/78/214/images/image208_0.gif" width="48" height="12"> и т. д.
Треугольный определитель - это тот определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали - нули, равен произведению элементов главной диагонали.
http://pandia.ru/text/78/214/images/image210_0.gif" width="37" height="28 src=">.gif" width="13 height=25" height="25">)
Обозначим ∆ =det A. Для того, чтобы квадратная Матрица А имела обратную, необходимо и достаточно, чтобы Матрица была не вырожденной (отличной от нуля). Матрица, обратная матрице А, обозначается через А-1, так что В = А-1. Обратная матрица вычисляется по формуле:C p - расстояние от начала координат до плоскости.
http://pandia.ru/text/78/214/images/image248.gif" width="110" height="36 src=">
Здесь http://pandia.ru/text/78/214/images/image250.gif" width="29" height="13"> произвольно, если D = 0 .
21. Кривые 2-го (уравнение окружности).
Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.
Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс , при пересечении образующих обеих полостей – гипербола , а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола .
Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.
Классификация кривых второго порядка
Невырожденные кривые
невырожденной , если Могут возникать следующие варианты:
Невырожденная кривая второго порядка называется центральной, если
· эллипс - при условии D > 0 и ΔI < 0;
частный случай эллипса - окружность - при условии I 2 = 4D или a 11 = a 22,a 12 = 0;
мнимый эллипс (ни одной вещественной точки) - при условии ΔI > 0;
· гипербола - при условии D < 0;
Невырожденная кривая второго порядка называется нецентральной, если ΔI = 0
· парабола - при условии D = 0.
Вырожденные кривые: Кривая второго порядка называется вырожденной , если Δ = 0. Могут возникать следующие варианты:
· вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) - при условии D > 0;
· пара вещественных пересекающихся прямых (вырожденная гипербола) - при условии D < 0;
· вырожденная парабола - при условии D = 0:
· пара вещественных параллельных прямых - при условии B < 0;
· одна вещественная прямая (две слившиеся параллельные прямые) - при условии B = 0;
· пара мнимых параллельных прямых (ни одной вещественной точки) - при условии B > 0.
22. Эллипс и его уравнение.
Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами , есть величина постоянная.
Замечание. При совпадении точек F 1 и F 2 эллипс превращается в окружность.
Выведем уравнение эллипса, выбрав декартову систему: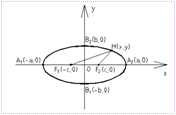 
координат так, чтобы ось Ох
совпала с прямой F
1F
2, начало координат – с серединой отрезка F
1F
2.
Пусть длина этого отрезка равна 2с , тогда в выбранной системе координат F 1(-c , 0), F 2(c , 0). Пусть точка М(х, у ) лежит на эллипсе, и сумма расстояний от нее до F 1 и F 2 равна 2а .
Тогда r 1 + r 2 =2a , но http://pandia.ru/text/78/214/images/image255.gif" width="103" height="25 src="> ,
Поэтомуhttp://pandia.ru/text/78/214/images/image257.gif" width="60" height="35 src="> (11.1)
Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а (11.2)
Определение 11.4. Директрисой Di эллипса, отвечающей фокусу Fi , называется прямая, расположенная в одной полуплоскости с Fi относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.
Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.
Свойства эллипса:
1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a >2b ), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.
2) Весь эллипс содержится внутри прямоугольника http://pandia.ru/text/78/214/images/image029_18.gif" width="12" height="19 src=">
3) Эксцентриситет эллипса e < 1.
Гипербола. Определение 11.5. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F 1 и F 2 этой плоскости, называемых фокусами , есть величина постоянная.http://pandia.ru/text/78/214/images/image265.gif" width="180" height="29">. Если обозначить b ² = c ² - a ², отсюда можно получить http://pandia.ru/text/78/214/images/image267.gif" width="38" height="30 src=">.gif" width="87" height="44 src="> , (11.3`)
для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.
4) Эксцентриситет гиперболы e > 1.
5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.
Доказательство можно провести так же, как и для эллипса.
23. Парабола.
Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой .
Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина перпендикуляра FD , опущенного из фокуса на директрису, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD
D O F x равна р . Тогда из равенства r = d следует, что http://pandia.ru/text/78/214/images/image271.gif" width="101 height=38" height="38">,
Алгебраическими преобразованиями это уравнение можно привести к виду:
y ² = 2px , (11.4) называемому каноническим уравнением параболы .
Величина р называется параметром параболы.
Свойства параболы :
1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.
2) Вся парабола расположена в правой полуплоскости плоскости Оху.
Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:
Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e <1), гиперболу (при e >1) или параболу (при е =1).
Приведение уравнения второго порядка к каноническому виду.
Определение 11.9. Линия, определяемая общим уравнением второго порядка
http://pandia.ru/text/78/214/images/image274.gif" width="103 height=19" height="19"> можно задать матрицу
http://pandia.ru/text/78/214/images/image276.gif" width="204" height="24 src="> (в предположении, что λ 1,2 не равны 0).
Зададим последующий параллельный перенос формулами: , .
Получим в новой координатной системе уравнение . (11.7)
Рассмотрим возможные геометрические образы, определяемые этим уравнением в зависимости от знаков λ
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX , OY и OZ . Оси координат пересекаются в точке O , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX - ось абсцисс, OY - ось ординат, OZ - ось аппликат.
Если большой палец правой руки принять за направление X , указательный за направление Y , а средний за направление Z , то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY , если этот поворот наблюдать со стороны положительного направления оси OZ . Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2).
Положение точки A в пространстве определяется тремя координатами x , y и z . Координата x равна длине отрезка OB , координата y - длине отрезка OC , координата z - длине отрезка OD в выбранных единицах измерения. Отрезки OB , OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ , XOZ и XOY соответственно. Координата x называется абсциссой точки A , координата y - ординатой точки A , координата z - аппликатой точки A . Записывают так: .
