Trojni integral je zapisan takole:

Izračunaj trojni integral - pomeni iskanje števila, ki je enako prostornini telesa V ali, kar je isto - območja V .

Skoraj vsak lahko razume pomen izračuna trojnega integrala "na težji način". Natančneje - "pod kožo", še natančneje - v njegovih dihalnih organih - pljučih. Ne glede na to, ali veste ali ne, je v človeških pljučih več kot 700 milijonov pljučnih mehurčkov – vezikularnih tvorb, prepletenih z mrežo kapilar. Izmenjava plinov poteka skozi stene alveolov. Zato lahko razmišljamo takole: prostornino plina v pljučih lahko predstavimo kot neko kompaktno območje. Ta volumen je sestavljen iz majhnih volumnov, koncentriranih v alveolih. Ključno vlogo v tej primerjavi igra ogromno število alveolov v pljučih: kot bomo videli v naslednjem odstavku, je skozi tako »ogromno število malenkosti« matematično oblikovan koncept trojnega integrala.

Zakaj se za določanje prostornine telesa uporablja trojni integral? V? Naj območje V razdeljen v n poljubna območja Δ vjaz, in ta oznaka ne pomeni le vsakega majhnega območja, temveč tudi njegovo prostornino. V vsakem tako majhnem območju je izbrana poljubna točka Mjaz, A f(Mjaz)- vrednost funkcije f(M) na tej točki. Zdaj bomo povečali število takšnih majhnih površin in največji premer Δ vjaz- nasprotno, zmanjšati. Sestavimo lahko integralno vsoto oblike

Če funkcija f(M) = f(x, l, z) je kontinuirano, bo obstajalo meja integralne vsote zgoraj navedeno vrsto. Ta meja se imenuje trojni integral .

V tem primeru funkcija f(M) = f(x, l, z) imenovan domensko integrabilen V ; V- območje integracije; x, l, z- integracijske spremenljivke, dv(oz dx dy dz ) - element glasnosti.

Izračun trojnega integrala z zmanjševanjem mnogokratnosti

Tako kot pri dvojnih integralih se izračun trojnih integralov zmanjša na izračun integralov nižje mnogokratnosti.

Razmislite o tridimenzionalni regiji V. Spodaj in zgoraj (torej po višini) je to območje omejeno s površinami z = z1 (x, l) in z = z2 (x, l) . Ob straneh (to je v širini) je območje omejeno s površinami l = l1 (x) in l = l2 (x) . In končno, v globino (če gledate območje v smeri osi Ox) - površine x = a in x = b

Za uporabo prehoda na integrale nižje mnogokratnosti je potrebno tridimenzionalno področje V je bil pravilen. Pravilno je, če je premica vzporedna z osjo Oz, prečka mejo regije V na največ dveh točkah. Pravilna tridimenzionalna območja so na primer kvader, elipsoid in tetraeder. Spodnja slika prikazuje pravokotni paralelepiped, ki ga bomo srečali v prvem primeru reševanja naloge.

Za vizualizacijo razlike med pravilnostjo in nepravilnostjo dodamo, da površine regije vzdolž višine pravilne regije ne smejo biti konkavne navznoter. Spodnja slika je primer nepravilnega območja V- enolistni hiperboloid, katerega površina je ravna, vzporedna z osjo Oz(rdeča), seka v več kot dveh točkah.

Upoštevali bomo samo pravilna področja.

Torej območje V- pravilno. Potem za katero koli funkcijo f(x, l, z) , neprekinjeno v regiji V, formula velja

Ta formula vam omogoča, da zmanjšate izračun trojnega integrala na zaporedni izračun notranjega določenega integrala nad spremenljivko z(konstantno x in l) in zunanji dvojni integral nad dvodimenzionalno domeno D .

Če preidemo od dvojnega integrala do ponovljenega, dobimo naslednjo formulo za izračun trojnega integrala:

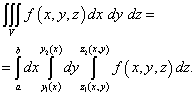
Za izračun trojnega integrala morate torej zaporedno ovrednotiti tri določene integrale.

Ti integrali se izračunajo od najbolj notranjih (čez spremenljivko z) na najbolj oddaljeno (po spremenljivki x). Za lažje razumevanje zaporedja izračunov lahko tri "vgnezdene" integrale zapišemo na naslednji način:

.

Že iz tega zapisa je razvidno, da:

• najprej morate integrirati funkcijo f(x, l, z) po spremenljivki z in vzemite enačbe kot integracijske meje z = z1 (x, l) in z = z2 (x, l) površine, ki omejujejo območje V spodaj in zgoraj;
• l l = l1 (x) in l = l2 (x) površine, ki omejujejo območje V s stranic;
• integrirajte rezultat, dobljen v prejšnjem koraku, nad spremenljivko x in vzemite enačbe kot integracijske meje x = a in x = b površine, ki omejujejo območje V v globino.

Primer 1. Pojdimo od trojnega integrala k iteriranemu integralu

-

zaporedja treh določenih integralov. Ocenite ta ponavljajoči se integral.

rešitev. Izračun iteriranega integrala se vedno začne od zadnjega integrala:

.

Izračunajmo drugi integral – nad spremenljivko l:

.

x:

.

Odgovor: Ta ponovljeni integral in njemu pripadajoči trojni integral sta enaka 10.

Primer 2. Izračunaj trojni integral

,

Kje V- paralelopiped, omejen z ravninami x = − 1 , x = + 1 , l = 0 , l = 1 , z = 0 , z = 2 .

rešitev. Meje integracije za vse tri določene integrale so enolično določene z enačbami površin, ki omejujejo paralelepiped. Zato ta trojni integral takoj reduciramo na zaporedje treh določenih integralov:

.

z

.

Integral izračunamo "na sredini" - nad spremenljivko l. Dobimo;

.

Zdaj izračunamo najbolj zunanji integral - nad spremenljivko x:

Odgovor: Ta trojni integral je -2.

Primer 3. Izračunaj trojni integral

,

Kje Vx + l + z = 1 in koordinatne ravnine x = 0 , l = 0 , z= 0. Regija V projiciran na ravnino xOy v trikotnik D, kot je prikazano na spodnji sliki.

rešitev. Najprej postavimo meje integracije. Za integral nad spremenljivko z spodnja meja integracije je enolično določena: z= 0. Da dobimo zgornjo mejo, izražamo z od x + l + z = 1 . Dobimo 1 − x − l. Za integral nad spremenljivko l spodnja meja integracije je enolično določena: l= 0. Za pridobitev zgornje meje izrazimo l od x + l + z = 1 , ob upoštevanju tega z= 0 (ker se premica nahaja v ravnini xOy). Dobimo: 1 − x .

Ta trojni integral zmanjšamo na zaporedje treh določenih integralov:

.

Izračunamo najbolj notranji integral – nad spremenljivko z, ob upoštevanju konstant x in y. Dobimo:

.

l. Dobimo:

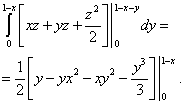
x:

Odgovor: Ta trojni integral je enak 1/8.

Sami izračunajte trojni integral in nato poglejte rešitev

Primer 4. Izračunaj trojni integral

,

Kje V- piramida, omejena z ravnino x + l + z = 1 in koordinatne ravnine x = 0 , l = 0 , z = 0 .

Ureditev integracijskih limit pri prehodu na zaporedje treh integralov

Zgodi se, da se učenci, ki nimajo posebnih težav pri neposrednem računanju integralov, ne morejo navaditi na postavljanje limitov integracije pri prehodu s trojnega integrala na zaporedje treh določenih integralov. Ta zadeva zahteva nekaj usposabljanja. V prvem primeru domena integracije V je bil paralelepiped, s katerim je vse jasno: z vseh strani je omejen z ravninami, kar pomeni, da so meje integracije enolično določene z enačbami ravnin. V drugem primeru - piramida: tu je bilo že treba malo bolj razmisliti in izraziti eno od mej iz enačbe. In če območje V ali jih omejujejo neravne površine? Območje je seveda potrebno na določen način pregledati V .

Začnimo z "bolj groznim" primerom, da bi občutili "situacijo blizu boja."

Primer 5. Uredite meje integracije pri prehodu iz trojnega integrala, v katerem regija V- elipsoid

.

rešitev. Naj bo središče elipsoida izhodišče, kot je prikazano na zgornji sliki. Poglejmo elipsoid od spodaj. Od spodaj je omejen s površino, ki je tisti del površine elipsoida, ki se nahaja pod ravnino xOy z in dobljeni izraz z znakom minus bo spodnja meja integracije nad spremenljivko z:

.

Zdaj pa poglejmo elipsoid od zgoraj. Tukaj je omejena s površino, ki je tisti del površine elipsoida, ki se nahaja nad osjo xOy. Zato moramo izraziti iz enačbe elipsoida z in dobljeni izraz bo zgornja meja integracije nad spremenljivko z:

.

Projekcija elipsoida na ravnino xOy je elipsoid. Njegova enačba:

Za pridobitev spodnje meje integracije nad spremenljivko l, je treba izraziti l iz elipsoidne enačbe in vzemite dobljeni izraz z znakom minus:

.

Za zgornjo mejo integracije nad spremenljivko l isti izraz z znakom plus:

Glede integracije nad spremenljivko x, nato območje V globinsko omejena z ravninami. Zato so meje integracije nad spremenljivko x lahko predstavimo kot koordinate zadnje in sprednje meje območja. V primeru elipsoida bodo to vrednosti dolžin pol osi, vzete z negativnimi in pozitivnimi predznaki a: x1 = − a in x2 = a .

Tako je zaporedje integralov za izračun prostornine elipsoida naslednje:

,

kjer so "yrek prvi", "yrek drugi", "zet prvi" in "zet drugi" zgoraj dobljeni izrazi. Če imate željo in pogum izračunati ta integral in s tem prostornino elipsoida, potem je tukaj odgovor: 4 πabc/3 .

Naslednji primeri niso tako strašljivi kot pravkar obravnavani. Poleg tega ne vključujejo le postavljanja meja integracije, ampak tudi izračun samega trojnega integrala. Preizkusite, kaj ste se naučili, tako da sledite rešitvi grozljivega primera. Še vedno morate razmišljati, ko postavljate meje.

Primer 6. Izračunaj trojni integral

če je integracijska domena omejena z ravninami x + l = 1 , x + 2l = 4 , l = 0 , l = 1 , z = 1 , z = 5 .

rešitev. Primer »letovišča« primerjamo s primerom 5, saj so meje integracije nad »Y« in »Z« enolično določene. Vendar se bomo morali ukvarjati z omejitvami integracije nad "X". Projekcija domene integracije na ravnino xOy je trapez ABCD.

V tem primeru je ugodneje projicirati trapez na os Oj, sicer boste morali za izračun trojnega integrala sliko razdeliti na tri dele. V primeru 4 smo integracijsko regijo začeli pregledovati od spodaj in to je običajen postopek. Toda v tem primeru začnemo pregled od strani ali, če je lažje, postavimo figuro na stran in menimo, da jo gledamo od spodaj. Meje integracije nad "X" lahko najdemo čisto algebraično. Da bi to naredili, izrazimo "x" iz prve in druge enačbe, podane v primeru pogoja. Iz prve enačbe dobimo spodnjo mejo 1 − l, od drugega - zgornji 4 − 2 l. Zmanjšajmo ta trojni integral na zaporedje treh določenih integralov:

.

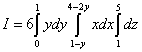Pozor! V tem primeru skrajni integral ni nad spremenljivko "x", temveč nad spremenljivko "y", "povprečni" integral pa je nad spremenljivko "x"! Tu smo uporabili spremembo vrstnega reda integracije, ki smo jo spoznali pri preučevanju dvojnega integrala. To je posledica dejstva, da smo, kot že omenjeno, integracijsko regijo začeli preučevati ne od spodaj, ampak od strani, to je, da je nismo projicirali na os Ox, na os Oj.

Izračunamo najbolj notranji integral – nad spremenljivko z, ob upoštevanju konstant x in y. Dobimo:

Izračunamo povprečni integral – po spremenljivki x. Dobimo:

.

Na koncu izračunamo še zunanji integral – nad spremenljivko l:

Odgovor: Ta trojni integral je enak 43.

Primer 7. Izračunaj trojni integral

,

če je območje integracije omejeno na površine x = 0 , l = 0 , z = 2 , x + l + z = 4 .

rešitev. Regija V(piramida MNRP) je pravilen. Območje projekcije V do letala xOy je trikotnik AOB.

Spodnje meje integracije za vse spremenljivke so podane v primeru pogoja. Poiščimo zgornjo mejo integracije nad "X". Da bi to naredili, izrazimo "x" iz četrte enačbe, pri čemer menimo, da je "y" enak nič in "ze" enak dve. Dobimo x= 2. Poiščimo zgornjo mejo integracije nad "igro". Če želite to narediti, izrazimo "Y" iz iste četrte enačbe, pri čemer menimo, da je "Z" enak dve in "X" kot spremenljiva vrednost. Dobimo l = 2 − x. In končno, najdemo zgornjo mejo integracije nad spremenljivko "z". Če želite to narediti, izrazimo "zet" iz iste četrte enačbe, pri čemer menimo, da sta "y" in "zet" spremenljivi količini. Dobimo z = 4 − x − l .

Zmanjšajmo ta trojni integral na zaporedje treh določenih integralov:

.

Izračunamo najbolj notranji integral – nad spremenljivko z, ob upoštevanju konstant x in y. Dobimo:

.

Izračunamo povprečni integral – po spremenljivki l. Dobimo:

.

Izračunamo najbolj zunanji integral – nad spremenljivko x in končno najdemo ta trojni integral:

Odgovor: Ta trojni integral je enak 2.

Sprememba spremenljivk v trojnem integralu in cilindričnih koordinatah

Če je projekcija integracijske domene na katero koli od koordinatnih ravnin krog ali del kroga, potem je trojni integral lažje izračunati s prehodom na cilindrične koordinate. Cilindrični koordinatni sistem je posplošitev polarni koordinatni sistem v vesolje. V cilindričnem koordinatnem sistemu je točka M označen s tremi količinami ( r, φ , z), Kje r- razdalja od izhodišča do projekcije n točke M do letala xOy, φ - kot med vektorjem VKLOP in pozitivno smerjo osi Ox, z- točka nanosa M(slika spodaj).

Pravokotne koordinate x, l, z s cilindričnimi koordinatami r, φ , z povežite formule

x = r cos φ ,

l = r greh φ ,

z = z .

Če se želite premakniti na cilindrične koordinate v trojnem integralu, morate izraziti integrand kot funkcijo spremenljivk r, φ , z:

To pomeni, da se prehod iz pravokotnih v cilindrične koordinate izvede na naslednji način:

Trojni integral v cilindričnih koordinatah izračunamo na enak način kot v kartezičnih pravokotnih koordinatah, tako da ga pretvorimo v zaporedje treh določenih integralov:

Primer 8. Izračunaj trojni integral

prehod v cilindrične koordinate, kjer V- območje, omejeno s površinami in.

rešitev. Ker območje V do letala xOy se projicira v krog, nato koordinata φ variira od 0 do 2 π , in koordinata r- od r=0 do r=1. Stalna vrednost v prostoru ustreza valju. Ob upoštevanju presečišča tega valja z regijo V, dobimo spremembo ordinate z od z = r do z= 1. Pojdimo na cilindrične koordinate in dobimo.

Transformacija dvojnega integrala pravokotnih koordinat, na polarne koordinate
, povezane s pravokotnimi koordinatami z relacijami
,
, se izvaja po formuli

Če domena integracije
omejena na dva žarka
,
(
), ki prihaja iz pola, in dve krivulji
in
, potem se dvojni integral izračuna po formuli

.

Primer 1.3. Izračunajte površino figure, ki jo omejujejo te črte:
,
,
,
.

rešitev. Za izračun površine območja
Uporabimo formulo:
.

Narisujmo območje (slika 1.5). Da bi to naredili, transformiramo krivulje: , , , . Preidimo na polarne koordinate: , . . V polarnem koordinatnem sistemu območje opisujejo enačbe:

.

1.2. Trojni integrali

Osnovne lastnosti trojnih integralov so podobne lastnostim dvojnih integralov.

V kartezičnih koordinatah je trojni integral običajno zapisan takole:

.

če
, nato pa trojni integral nad območjem številčno enaka prostornini telesa :

.

Izračun trojnega integrala

Naj domena integracije omejeni spodaj oziroma zgoraj z zveznimi ploskvami z eno vrednostjo
,
, in projekcijo regije na koordinatno ravnino
tam je ravno območje
(slika 1.6).

Potem za fiksne vrednosti ustrezne aplikacije točke območja razlikujejo znotraj. Potem dobimo: . Če poleg tega projekcija določen z neenakostmi , , Kje - zvezne funkcije z eno vrednostjo vklopljene , To

.

Primer 1.4. Izračunaj
, Kje - telo, omejeno z ravninami:

	, , , ( , , ). rešitev. Območje integracije je piramida (slika 1.7). Območje projekcije obstaja trikotnik , omejeno z ravnimi črtami , , (slika 1.8). pri velja pika zadovoljiti neenakost , Zato .
	Nastavitev meja integracije za trikotnik , dobimo

Trojni integral v cilindričnih koordinatah

Pri premikanju iz kartezičnih koordinat
na cilindrične koordinate
(Sl. 1.9), povezane z
odnosov
,
,
, in

	, ,, trojni integral se transformira: Primer 1.5. Izračunajte prostornino telesa, ki ga omejujejo površine: , , . rešitev. Zahtevana prostornina telesa enako .
	Integracijska domena je del valja, ki je spodaj omejen z ravnino , in nad ravnino (slika 1.10). Območje projekcije tam je krog s središčem v izhodišču in enotskim polmerom. Preidimo na cilindrične koordinate. , , . pri velja pika , zadovoljiti neenakost ali v cilindričnih koordinatah:

Regija
, omejeno s krivuljo
, bo dobila obliko, oz
, medtem ko je polarni kot
. Kot rezultat imamo

.

2. Elementi teorije polja

Najprej se spomnimo metod za izračun krivuljnih in površinskih integralov.

Izračun krivuljnega integrala nad koordinatami funkcij, definiranih na krivulji , zmanjša na izračun določenega integrala oblike

če je krivulja določeno parametrično
ustreza začetni točki krivulje , A
- njegova končna točka.

Izračun površinskega integrala funkcije
, definirana na dvostranski površini , se zmanjša na izračun dvojnega integrala, na primer, oblike

,

če je površina , podana z enačbo
, je edinstveno projiciran na ravnino
v regijo
. Tukaj - kot med enotskim normalnim vektorjem na površje in os
:

.

Stran površine, ki jo zahtevajo problemski pogoji je določena z izbiro ustreznega predznaka v formuli (2.3).

Opredelitev 2.1. Vektorsko polje
imenujemo vektorska funkcija točke
skupaj s svojim obsegom:

Vektorsko polje
označen s skalarno količino – razhajanje:

Opredelitev 2.2. Tok vektorsko polje
skozi površino imenovan površinski integral:

,

Kje - enotski normalni vektor na izbrano stran površine , A
- skalarni produkt vektorjev in .

Opredelitev 2.3. Naklada vektorsko polje

Avtor: zaprta krivulja imenovan krivuljični integral

,

Kje
.

Formula Ostrogradsky-Gauss vzpostavlja povezavo med tokom vektorskega polja skozi zaprto površino in divergenca polja:

Kje - površina, omejena z zaprto konturo , A je enotski normalni vektor na to površino. Smer normale mora biti skladna s smerjo prečkanja konture .

Primer 2.1. Izračunaj površinski integral

,

Kje - zunanji del stožca
(
), odrezana z letalom
(Slika 2.1).

rešitev. Površina edinstveno projiciran v regijo
letalo
, integral pa izračunamo s formulo (2.2).

Normalni vektor enotske površine najdemo s formulo (2.3): . Tukaj je v izrazu za normalo izbran znak plus, saj je kot med osjo in normalno - neumno in zato mora biti negativno. Glede na to , na površini dobimo

Regija
tam je krog
. Zato se v zadnjem integralu premaknemo na polarne koordinate, medtem ko
,
:

Primer 2.2. Poiščite divergenco in ukrivljenost vektorskega polja
.

rešitev. Z uporabo formule (2.4) dobimo

Rotor danega vektorskega polja najdemo s formulo (2.5)

Primer 2.3. Poiščite tok vektorskega polja
skozi del letala :
, ki se nahaja v prvem oktantu (normala tvori oster kot z osjo
).

	rešitev. Na podlagi formule (2.6) . Upodabljajmo del letala : , ki se nahaja v prvem oktantu. Enačba te ravnine v segmentih ima obliko (slika 2.3). Normalni vektor na ravnino ima koordinate: , enotni normalni vektor
	. . , , kje , torej,

Kje
- ravninska projekcija na
(slika 2.4).

Primer 2.4. Izračunajte tok vektorskega polja skozi zaprto površino , ki ga tvori ravnina
in del stožca
(
) (slika 2.2).

rešitev. Uporabimo formulo Ostrogradsky-Gauss (2.8)

.

Poiščimo divergenco vektorskega polja po formuli (2.4):

Kje
je prostornina stožca, nad katerim se izvaja integracija. Za izračun prostornine stožca uporabimo dobro znano formulo
(- polmer osnove stožca, - njegova visoka). V našem primeru dobimo
. Končno dobimo

.

Primer 2.5. Izračunajte cirkulacijo vektorskega polja
po konturi , ki nastane zaradi presečišča površin
in
(
). Preverite rezultat s Stokesovo formulo.

rešitev. Presek teh ploskev je krog
,
(slika 2.1). Smer prečkanja je običajno izbrana tako, da območje, ki ga omejuje, ostane levo. Zapišimo parametrične enačbe konture :

kje

in parameter razlikuje od prej
. Z uporabo formule (2.7) ob upoštevanju (2.1) in (2.10) dobimo

.

Uporabimo zdaj Stokesovo formulo (2.9). Kot površina , raztegnjen na konturi , lahko vzamete del letala
. Normalna smer
na to površino je skladna s smerjo prečkanja konture . Curl danega vektorskega polja je izračunan v primeru 2.2:
. Zato je želena cirkulacija

Kje
- območje regije
.
- polmer kroga
, kje

Naj bo dano snovno telo, ki je prostorsko območje P, napolnjeno z maso. Potrebno je najti maso m tega telesa, če je v vsaki točki P € P znana gostota porazdelitve mase. Razdelimo površino P na neprekrivajoče se kubične (tj. z volumnom) dele z volumni. V vsakem od delnih območij ft* izberemo poljubno točko P*. Predpostavimo približno, da je znotraj delnega območja ft* gostota konstantna in enaka /*(P*). Tedaj bo masa Atk tega dela telesa izražena s približno enakostjo Atpk in masa celega telesa bo približno enaka Trojni integral Lastnosti trojnih integralov Izračun trojnega integrala v kartezičnih koordinatah Izračun trojnega integrala v cilindrične in sferične koordinate. Naj bo d največji od premerov delnih območij. Če ima pri d -* 0 vsota (1) končno mejo, ki ni odvisna niti od metode razdelitve domene ft na delne poddomene niti od izbira točk P* ∈ ft*, potem je ta meja vzeta kot masa danega telesa m. Naj bo omejena funkcija definirana v zaprti kubni domeni ft ft na n kockastih delov, ki se ne sekajo, njihove prostornine pa so označene z oz. . V vsakem delnem podobmočju P* poljubno izberemo točko Pk(xk, yk, zk) in sestavimo integralno vsoto, pri čemer naj bo d največji izmed premerov delnih območij Definicija. Če imajo za d 0 integralne vsote a mejo, ki ni odvisna niti od metode razdelitve domene A na delne poddomene Π* niti od izbire točk Pk ∈ Π*, potem se ta meja imenuje triadni integral od funkcijo f(x) y, z) nad domeno Q in jo označimo s simbolom. Izrek 6. Če je funkcija f(x, y, z) zvezna v zaprti kubni domeni Π, potem je v tej domeni integrabilna. Lastnosti trojnih integralov Lastnosti trojnih integralov so podobne lastnostim dvojnih integralov, naštejmo glavne. Naj bodo funkcije integrabilne v kubni domeni L. 1. Linearnost. V tem primeru se funkcija imenuje integrabilna v domeni Q. Tako imamo po definiciji. Če se vrnemo k problemu izračuna mase telesa, opazimo, da je limita (2) trojni integral funkcije p(P) nad domeno P. To pomeni, Tukaj dx dy dz - prostorninski element dv v pravokotnih koordinatah. kjer sta a in (3 poljubni realni konstanti povsod v domeni P, potem je 3. Če je /(P) = 1 v domeni P, potem je n, kjer je V prostornina domene Q. Če je funkcija /(P) neprekinjeno v zaprti kubični domeni ft in M ​​in m sta njegovi največji in najmanjši vrednosti v ft, kjer je V prostornina površine ft. 5. Aditivnost. Če je domena ft razdeljena na kubične domene brez skupnih notranjih točk in je f(P) integrabilen v domeni ft, potem je f(P) integrabilen na vsaki od domen ft| in ft2, s 6. Izrek o srednji vrednosti. Izrek 7 (o srednji vrednosti). Če je funkcija f(P) zvezna v zaprti kubni domeni ft, potem obstaja tona Pc € ft, tako da velja formula: kjer je V prostornina domene ft (spomnimo se, da je domena povezana množica) . § 7. Izračun trojnega integrala v kartezičnih koordinatah Tako kot pri izračunu dvojnih integralov gre tudi tukaj za izračun ponovljenih integralov. Predpostavimo, da je funkcija zvezna v neki domeni ft. 1. primer. Območje ft je pravokoten paralelepiped, projiciran na ravnino yOz v pravokotnik i2; Nato dobimo Z zamenjavo dvojnega integrala s ponovljenim končno dobimo Tako smo v primeru, ko je območje P pravokotni paralelopiped, izračun trojnega integrala zmanjšali na zaporedni izračun treh navadnih integralov. Formulo (2) lahko prepišemo v obliki, kjer je pravokotnik pravokotna projekcija paralelopipeda P na ravnino xOy. 2. primer. Oglejmo si zdaj območje Q tako, da površina 5, ki ga omejuje, seka katero koli ravno črto, vzporedno z osjo Oz, v največ dveh točkah ali vzdolž celotnega segmenta (slika 22). Naj bo z = tpi(x,y) enačba površine 5, ki omejuje območje P od spodaj, in naj ima površina S2, ki omejuje območje P od zgoraj, enačbo z = y). Naj sta obe ploskvi S\ in S2 projicirani na isto področje ravnine xOy. Označimo ga z D, krivuljo, ki ga omejuje, pa z L. Preostali del meje 5 telesa Q leži na valjasti ploskvi z generatorjami, vzporednimi z osjo Oz, in s krivuljo L kot vodilom. Nato po analogiji s formulo (3) dobimo. Če je območje D ravnine xOy krivolinijski trapez, omejen z dvema krivuljama, potem lahko dvojni integral v formuli (4) reduciramo na ponovljenega in končno dobimo Ta formula je posplošitev formule (2). Slika-23 Primer. Izračunajte prostornino tetraedra, omejenega z ravninami. Projekcija tetraedra na ravnino xOy je trikotnik, ki ga tvorijo ravne črte, tako da se x spreminja od 0 do 6, pri fiksnem x (0 ^ x ^ 6) pa se y spreminja od 0 do 3 - | (Slika 23). Če sta oba x in y fiksna, se lahko točka navpično premika od ravnine do ravnine in se spreminja v območju od 0 do 6 - x - 2y. Z uporabo formule dobimo §8. Izračun trojnega integrala v cilindričnih in sferičnih koordinatah Vprašanje spreminjanja spremenljivk v trojnem integralu rešujemo na enak način kot v primeru dvojnega integrala. Naj bo funkcija f(x, y, z) zvezna v zaprti kubni domeni ft in naj bodo funkcije zvezne skupaj s svojimi parcialnimi odvodi prvega reda v zaprti kubni domeni ft*. Predpostavimo, da funkcije (1) vzpostavljajo korespondenco ena proti ena med vsemi točkami rj, () področja ft* na eni strani in vsemi točkami (zh, y, z) področja ft na drugi. Takrat velja formula za spreminjanje spremenljivk v trojnem integralu: kjer je jakobian sistema funkcij (1). V praksi pri izračunu trojnih integralov pogosto uporabljajo zamenjavo pravokotnih koordinat s cilindričnimi in sferičnimi koordinatami. 8.1. Trojni integral v cilindričnih koordinatah V cilindričnem koordinatnem sistemu je položaj točke P v prostoru določen s tremi števili p, kjer sta p in (p polarni koordinati projekcije P1 točke P na ravnino xOy, z pa je nanašamo na točko P (slika 24). Števila imenujemo cilindrične koordinatne točke R. Jasno je, da so v sistemu cilindričnih koordinat koordinatne ploskve Trojni integral Lastnosti trojnih integralov Izračun trojnega integrala v kartezičnih koordinatah Izračun trojni integral v cilindričnih in sferičnih koordinatah opisujejo: krožni valj, katerega os sovpada z osjo Oz, polravnina, ki meji na os Oz, in ravnina, vzporedna z ravnino xOy. Cilindrične koordinate so povezane z naslednje kartezične formule (glej sliko 24). Za sistem (3), ki preslikava regijo ft na regijo, imamo tudi formulo (2) za prehod od trojnega integrala v pravokotnih koordinatah k integralu v v cilindričnih koordinatah oblika (4) Izraz imenujemo prostorninski element v cilindričnih koordinatah. Ta izraz za prostorninski element lahko dobimo tudi iz geometrijskih premislekov. Razdelimo področje P na elementarna podobmočja s koordinatnimi ploskvami in izračunajmo prostornine nastalih krivuljnih prizem (slika 25). Vidimo lahko, da Če zavrnemo infinitezimalno količino višjega reda, dobimo To nam omogoča, da vzamemo naslednjo količino kot prostorninski element v cilindričnih koordinatah Primer 1. Poiščite prostornino telesa, omejenega s površinami 4 V cilindričnih koordinatah dane površine bo imela enačbe (glej formule (3)). Te ploskve se sekajo vzdolž premice r, ki je opisana s sistemom enačb (valj), (ravnina), slika 26 in njeno projekcijo na ravnino xOy s sistemom Tako se zahtevana prostornina izračuna po formuli (4), v ki. Trojni integral v sferičnih koordinatah V sferičnem koordinatnem sistemu je položaj točke P(x, y, z) v prostoru določen s tremi števili, kjer je r razdalja od izhodišča do točke, kot med osjo Ox in projekcija polmernega vektorja OR točke P na ravnino xOy, c pa je kot med osjo Oz in polmernim vektorjem OR točke P, merjeno od osi Oz (sl. 27). Jasno je, da. Koordinatne ploskve v tem koordinatnem sistemu: r = const - krogle s središčem v izhodišču; ip = const polravnine, ki izhajajo iz osi Oz; в = const - krožni stožci z osjo Oz. riž. 27 Iz slike je razvidno, da so sferične in kartezične koordinate povezane z naslednjimi razmerji: Izračunajmo jakobian funkcij (5). Imamo. Posledično ima formula (2) tudi obliko Volumski element v sferičnih koordinatah - Izraz za prostorninski element lahko dobimo tudi iz geometrijskih premislekov. Razmislimo o elementarnem območju v prostoru, ki ga omejujejo krogle polmerov r in r + dr, stožci b in b + d$ ter polravnine.Približno to območje lahko štejemo za pravokotni paralelepiped z dimenzijami. Nato Trojni integral Lastnosti trojnih integralov Izračun trojnega integrala v kartezičnih koordinatah Izračun trojnega integrala v cilindričnih in sferičnih koordinatah Primer 2. Poiščite prostornino konveksnega telesa Q, izrezanega iz stožca s koncentričnimi kroglami -4 Preidemo na sferični koordinatni sistem Iz prvih dveh enačb je razvidno, da. Iz tretje enačbe najdemo meje spremenjenega kota 9: od koder

Postopek za izračun trojnega integrala je podoben ustrezni operaciji za dvojni integral. Da bi ga opisali, uvedemo koncept pravilne tridimenzionalne regije:

Opredelitev 9.1. Tridimenzionalno območje V, ki ga omejuje zaprta površina S, se imenuje pravilno, če:

1. katera koli ravna črta, ki je vzporedna z osjo Oz in poteka skozi notranjo točko območja, seka S v dveh točkah;
2. celotno območje V je projicirano na ravnino Oxy v pravilno dvodimenzionalno območje D;
3. kateri koli del območja V, odrezan od njega z ravnino, ki je vzporedna s katero koli koordinatno ravnino, ima lastnosti 1) in 2).

Oglejmo si regularno območje V, omejeno spodaj in zgoraj s ploskvama z=χ(x,y) in z=ψ(x,y) in projicirano na ravnino Oxy v regularno območje D, znotraj katerega se x spreminja od a na b, omejeno s krivuljama y=φ1(x) in y=φ2(x) (slika 1). Definirajmo zvezno funkcijo f(x, y, z) v domeni V.

Opredelitev 9.2. Imenujmo trojni integral funkcije f(x, y, z) nad območjem V izraz v obliki:

Trojni integral ima enake lastnosti kot dvojni integral. Navajamo jih brez dokaza, saj jih dokazujemo podobno kot pri dvojnem integralu.

Izračun trojnega integrala.

Izrek 9.1. Trojni integral funkcije f(x,y,z) nad regularno domeno V je enak trojnemu integralu nad isto domeno:

. (9.3)

Dokaz.

Področje V razdelimo z ravninami, vzporednimi s koordinatnimi ravninami, na n pravilnih območij. Potem iz lastnosti 1 sledi, da

kjer je trojni integral funkcije f(x,y,z) nad območjem.

Z uporabo formule (9.2) lahko prejšnjo enakost prepišemo kot:

Iz pogoja zveznosti funkcije f(x,y,z) sledi, da limita integralne vsote na desni strani te enačbe obstaja in je enaka trojnemu integralu. Nato s prehodom na limit pri , dobimo:

Q.E.D.

Komentiraj.

Podobno kot v primeru dvojnega integrala je mogoče dokazati, da sprememba vrstnega reda integracije ne spremeni vrednosti trojnega integrala.

Primer. Izračunajmo integral, pri čemer je V trikotna piramida z oglišči v točkah (0, 0, 0), (1, 0, 0), (0, 1, 0) in (0, 0, 1). Njegova projekcija na ravnino Oxy je trikotnik z oglišči (0, 0), (1, 0) in (0, 1). Območje je od spodaj omejeno z ravnino z = 0, od zgoraj pa z ravnino x + y + z = 1. Preidimo na trikratni integral:

Faktorje, ki niso odvisni od integracijske spremenljivke, lahko vzamemo iz predznaka ustreznega integrala:

Krivočrtni koordinatni sistemi v tridimenzionalnem prostoru.

1. Cilindrični koordinatni sistem.

Cilindrične koordinate točke P(ρ,φ,z) so polarne koordinate ρ, φ projekcije te točke na ravnino Oxy in aplikate te točke z (slika 2).

Formule za prehod iz cilindričnih v kartezične koordinate lahko podamo na naslednji način:

x = ρ cosφ, y = ρ sinφ, z = z. (9,4)

1. Sferični koordinatni sistem.

V sferičnih koordinatah je položaj točke v prostoru določen z linearno koordinato ρ - razdaljo od točke do izhodišča kartezičnega koordinatnega sistema (ali pola sferičnega sistema), φ - polarni kot med pozitivnim pol osi Ox in projekcijo točke na ravnino Oxy ter θ - kot med pozitivno pol osjo osi Oz in segmentom OP (slika 3). pri čemer

Postavimo formule za prehod iz sferičnih v kartezične koordinate:

x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (9,5)

Jacobian in njegov geometrijski pomen.

Oglejmo si splošni primer spreminjanja spremenljivk v dvojnem integralu. Naj bo podano območje D v ravnini Oxy, omejeno s premico L. Predpostavimo, da sta x in y enovredni in zvezno diferenciabilni funkciji novih spremenljivk u in v:

x = φ(u, v), y = ψ(u, v). (9,6)

Oglejmo si pravokotni koordinatni sistem Ouv, katerega točka P΄(u, v) ustreza točki P(x, y) iz območja D. Vse take točke tvorijo območje D΄ v ravnini Ouv, omejeno z črta L΄. Lahko rečemo, da formule (9.6) vzpostavljajo eno proti ena korespondenco med točkama območij D in D΄. V tem primeru sta premici u = const in

v = const v ravnini Ouv bo ustrezal nekaterim premicam v ravnini Oxy.

Oglejmo si pravokotno območje ΔS΄ v ravnini Ouv, omejeno z ravnimi črtami u = const, u+Δu = const, v = const in v+Δv = const. Ustrezal bo ukrivljenemu območju ΔS v ravnini Oxy (slika 4). Območja obravnavanih območij bodo označena tudi z ΔS΄ in ΔS. V tem primeru je ΔS΄ = Δu Δv. Poiščimo območje ΔS. Označimo oglišča tega krivokotnega štirikotnika P1, P2, P3, P4, kjer

P1(x1, y1), x1 = φ(u, v), y1 = ψ(u, v);

P2(x2, y2), x2 = φ(u+Δu, v), y2 = ψ(u+Δu, v);

P3(x3, y3), x3 = φ(u+Δu, v+Δv), y3 = ψ(u+Δu, v+Δv);

P4(x4, y4), x4 = φ(u, v+Δv), y4 = ψ(u, v+Δv).

Zamenjajmo majhna prirastka Δu in Δv z ustreznimi diferenciali. Potem

V tem primeru lahko štirikotnik P1 P2 P3 P4 štejemo za paralelogram in njegovo ploščino lahko določimo s formulo iz analitične geometrije:

(9.7)

Opredelitev 9.3. Determinanto imenujemo funkcionalna determinanta ali Jacobian funkcij φ(x, y) in ψ(x, y).

S prehodom na limito pri v enačbi (9.7) dobimo geometrični pomen Jakobija:

to pomeni, da je modul Jacobiana meja razmerja površin infinitezimalnih površin ΔS in ΔS΄.

Komentiraj. Na podoben način lahko definiramo koncept Jakobijana in njegov geometrijski pomen za n-dimenzionalni prostor: če je x1 = φ1(u1, u2,…,un), x2 = φ2(u1, u2,…,un) ,…, xn = φ(u1 , u2,…, un), potem

(9.8)

V tem primeru modul Jacobiana daje mejo razmerju "volumenov" majhnih območij prostorov x1, x2,..., xn in u1, u2,..., un.

Sprememba spremenljivk v več integralih.

Preučimo splošni primer spremembe spremenljivk na primeru dvojnega integrala.

Naj bo v domeni D podana zvezna funkcija z = f(x,y), katere vsaka vrednost ustreza enaki vrednosti funkcije z = F(u, v) v domeni D΄, kjer

F(u, v) = f(φ(u, v), ψ(u, v)). (9,9)

Upoštevajte integralno vsoto

kjer je integralna vsota na desni prevzeta po domeni D΄. S prehodom na limit pri , dobimo formulo za transformacijo koordinat v dvojnem integralu.

Primeri rešitev poljubnih trojnih integralov.
Fizikalne aplikacije trojnega integrala

V 2. delu lekcije bomo obdelali tehniko reševanja poljubnih trojnih integralov , katerega integrand funkcija treh spremenljivk v splošnem primeru se razlikuje od konstantnega in neprekinjenega v regiji; in se tudi seznaniti s fizikalnimi aplikacijami trojnega integrala

Priporočam, da novi obiskovalci začnejo s 1. delom, kjer smo obravnavali osnovne pojme in problem iskanja prostornine telesa s pomočjo trojnega integrala. Ostalim predlagam, da malo ponovite. odvodi funkcij treh spremenljivk, saj bomo v primerih tega članka uporabili inverzno operacijo - delna integracija funkcije

Poleg tega obstaja še ena pomembna točka: če se ne počutite dobro, je bolje, da branje te strani odložite, če je mogoče. In bistvo ni samo v tem, da se bo kompleksnost izračunov zdaj povečala - večina trojnih integralov nima zanesljivih metod ročnega preverjanja, zato je zelo nezaželeno, da jih začnete reševati v utrujenem stanju. Za nizek ton je priporočljivo reši kaj lažjega ali pa se le sprostim (sem potrpežljiv, bom počakal =)), da bom kdaj drugič s svežo glavo nadaljeval s trojnimi integrali:

Primer 13

Izračunaj trojni integral

V praksi telo označujemo tudi s črko , vendar to ni zelo dobra možnost, saj je »ve« »rezerviran« za označevanje volumna.

Takoj vam povem, česa NE storiti. Ni potrebe po uporabi lastnosti linearnosti in predstavljajo integral v obliki . Čeprav, če res želite, potem lahko. Na koncu pa majhen plus – čeprav bo posnetek dolg, bo manj natrpan. Toda ta pristop še vedno ni standarden.

V algoritmu rešitve bo malo novosti. Najprej morate razumeti domeno integracije. Projekcija telesa na ravnino je boleče znan trikotnik:

Telo je omejeno od zgoraj letalo, ki poteka skozi izvor. Mimogrede, najprej morate obvezno preverite(miselno ali v osnutku), ali ta ravnina "odseka" del trikotnika. Da bi to naredili, najdemo njeno presečišče s koordinatno ravnino, tj. Rešujemo najpreprostejši sistem: - ne, ta naravnost (ni na risbi)»gre mimo«, projekcija telesa na ravnino pa res predstavlja trikotnik.

Tudi prostorska risba tukaj ni zapletena:

Pravzaprav se je dalo omejiti le na to, saj je projekcija zelo preprosta. ... No, ali samo risba projekcije, saj je tudi telo preprosto =) Vendar pa je, da ne narišete ničesar, vas spomnim, slaba izbira.

No, seveda si ne morem kaj, da vas ne razveselim s končno nalogo:

Primer 19

Poiščite težišče homogenega telesa, ki ga omejujejo površine, . Nariši risbe tega telesa in njegovo projekcijo na ravnino.

rešitev: želeno telo je omejeno s koordinatnimi ravninami in ravnino, ki je primerna za kasnejšo konstrukcijo prisoten v segmentih: . Izberimo "a" kot enoto merila in naredimo tridimenzionalno risbo:

Risba ima že pripravljeno težišče, vendar ga še ne poznamo.

Projekcija telesa na ravnino je očitna, vendar naj vas kljub temu spomnim, kako jo najti analitično - navsezadnje se tako preprosti primeri ne pojavljajo vedno. Če želite najti črto, vzdolž katere se ravnine sekata, morate rešiti sistem:

Nadomestimo vrednost v 1. enačbo: in dobimo enačbo "ravna" ravna:

S formulami izračunamo koordinate težišča telesa
, kjer je prostornina telesa.