Karakteristična enačba je sestavljena za vezje po preklopu. Pridobite ga lahko na naslednje načine:
Neposredno na podlagi diferencialne enačbe oblike (1.2), tj. z izključitvijo iz sistema enačb, ki opisujejo elektromagnetno stanje vezja na podlagi Kirchhoffovih zakonov, vse neznane količine, razen ene, v zvezi s katero je enačba zapisana;
Z uporabo izraza za vhodno impedanco tokokroga sinusnega toka;
Na podlagi izražanja glavne determinante.
Po prvi metodi v 1.4.1 smo dobili diferencialno enačbo za napetost u C na kondenzatorju za serijo r-L-C-verige (glej sliko 1.6):
na podlagi katerega je zapisana karakteristična enačba
.
Upoštevati je treba, da ker je linearno vezje zajeto z enim samim prehodnim procesom, so koreni karakteristične enačbe skupni vsem prostim komponentam napetosti in tokov vej vezja, katerih parametri so vključeni v karakteristično enačbo. Zato lahko po prvem načinu sestavljanja karakteristične enačbe izberemo poljubno količino kot količino, glede na katero je zapisana.
Sestavljanje karakteristične enačbe z uporabo metode vhodnega upora je naslednje:
1. Zapišite izraz za vhodni upor izmeničnega tokokroga v kompleksni obliki;
2. V nastalem izrazu jω zamenja operater R;
3. Dobljeni izraz je enak nič.
Enačba sovpada z značilno.
Poudariti je treba, da lahko vhodni upor zapišemo glede na prelomno točko katere koli veje vezja. V tem primeru so viri energije izključeni iz vezja, njihov notranji upor pa ostane na njihovem mestu.
Ta metoda sestavljanja karakteristične enačbe predpostavlja odsotnost magnetno sklopljenih vej v električnem tokokrogu. Če obstajajo, je potrebno izvesti magnetno ločitev.
Za obravnavano vezje (glej sliko 1.6) z uporabo metode vhodnega upora imamo:
;
;
.
Pri sestavljanju karakteristične enačbe na podlagi izraza glavne determinante je število algebraičnih enačb, na podlagi katerih je zapisana, enako številu neznanih komponent prostega toka.
Algebraizacija izvirnega sistema integro-diferencialnih enačb, sestavljenega na primer na podlagi Kirchhoffovih zakonov ali metode konturnih tokov, se izvede z zamenjavo operacij diferenciacije in integracije z množenjem in deljenjem z operatorjem R. Karakteristično enačbo dobimo tako, da zapisano determinanto enačimo z nič.
Ker izraz za glavno determinanto ni odvisen od desnih strani sistema nehomogenih enačb, ga lahko sestavimo na podlagi sistema enačb, zapisanih za skupne tokove.
Za obravnavano shemo (glej sliko 1.6) za prosti način imamo:
.
Z zamenjavo odvoda in integrala v enačbi, kot je navedeno zgoraj, dobimo algebraično enačbo
oz 
.
Od kod ga dobimo?
oz .
) A = ||a ik||n 1 z odštevanjem vrednosti λ od diagonalnih elementov. Ta determinanta je polinom glede na X – karakteristični polinom. Ko se odpre, X. u. je napisano takole:
Kje S 1 = a 11 + a 22 +... ann- tako imenovani matrična sled, S 2- vsota vseh večjih manjšnikov 2. reda, tj. manjšnikov oblike i k) itd., in S n- matrična determinanta A. Korenine H. u. λ 1 , λ 2 ,..., λ n se imenujejo lastne vrednosti matrike A. Za realno simetrično matriko, pa tudi za hermitsko matriko, so vsi λ k so realne, ima realna poševno-simetrična matrika vse λ kčisto namišljene številke; v primeru realne ortogonalne matrike, pa tudi enotne matrike, vsi |λ k| = 1.
H.u. najdemo na najrazličnejših področjih matematike, mehanike, fizike in tehnologije. V astronomiji pri ugotavljanju sekularnih motenj planetov pridejo tudi do kemijskih enačb; od tod drugo ime za X. u. - stara enačba.
2) H. u. linearna diferencialna enačba s konstantnimi koeficienti
a 0λ l (n) + 1 leto (n-1) +... + a n-1 y" + kaj = 0
Algebraična enačba, ki jo dobimo iz dane diferencialne enačbe po spremembi funkcije pri in njene odpeljanke z ustreznimi potencami λ, to je enačba
a 0λ n + a 1λ n-1 + ... + n-1 y" + kaj = 0.
Do te enačbe pridemo z iskanjem določene rešitve oblike pri = se λ X za dano diferencialno enačbo. Za sistem linearnih diferencialnih enačb
H.u. zapisano z uporabo determinanta
H.u. matrice A =
Velika sovjetska enciklopedija. - M.: Sovjetska enciklopedija. 1969-1978 .
Oglejte si, kaj je "Karakteristična enačba" v drugih slovarjih:
V mnogih primerih so fizični procesi, ki se pojavljajo v sistemih, opisani s sistemom navadnih linearnih diferencialnih enačb s konstantnimi koeficienti, ki jih je v dokaj splošnem primeru mogoče zmanjšati na diferencialno enačbo ... Enciklopedija tehnologije
Algebrska enačba oblike: determinanta v tej formuli se dobi iz determinante matrike z odštevanjem vrednosti x od diagonalnih elementov; predstavlja polinom v x in se imenuje karakteristični polinom... Veliki enciklopedični slovar
karakteristična enačba- - [V.A. Semenov. Angleško-ruski slovar relejne zaščite] Teme relejna zaščita EN karakteristična enačba ... Priročnik za tehnične prevajalce
Algebraična enačba oblike. Determinanto v tej formuli dobimo iz determinante matrike x diagonalnih elementov; je polinom v x in se imenuje karakteristični polinom. * * * ZNAČILNOST… … enciklopedični slovar
karakteristična enačba- būdingoji lygtis statusas T sritis avtomatika atitikmenys: engl. karakteristična enačba; enačba zmogljivosti vok. charakteristische Gleichung, f; Stammgleichung, f rus. karakteristična enačba, n pranc. équation caractéristique, f … Automatikos terminų žodynas
karakteristična enačba- būdingoji lygtis statusas T sritis fizika atitikmenys: engl. karakteristična enačba; enačba zmogljivosti vok. Charakteristische Gleichung, f rus. karakteristična enačba, n pranc. équation caractéristique, f … Fizikos terminų žodynas
karakteristična enačba Enciklopedija "Letalstvo"
karakteristična enačba- karakteristična enačba. V mnogih primerih so fizikalni procesi, ki se pojavljajo v sistemih, opisani s sistemom navadnih linearnih diferencialnih enačb s konstantnimi koeficienti, ki jih je v dokaj splošnem primeru mogoče zmanjšati ... Enciklopedija "Letalstvo"
Sekularna enačba, glej čl. Karakteristični polinom ... Matematična enciklopedija
Značilni polinom je polinom, ki določa lastne vrednosti matrike. Drug pomen: Značilni polinom linearne rekurente je polinom. Vsebina 1 Definicija ... Wikipedia
knjige
- Karakteristični Liejevi obroči in nelinearne integrabilne enačbe, Zhiber A.V.. Knjiga je posvečena sistematični predstavitvi algebraičnega pristopa k študiju nelinearnih integrabilnih parcialnih diferencialnih enačb in njihovih diskretnih analogov, ki temelji na konceptu...
Prosti način vezja ni odvisen od virov energije, določajo ga le struktura vezja in parametri njegovih elementov. Iz tega sledi, da bodo koreni karakteristične enačbe p1, p2,..., pn enaki za vse spremenljive funkcije (tokove in napetosti).
Značilno enačbo je mogoče sestaviti z različnimi metodami. Prva metoda je klasična, ko je značilna enačba sestavljena strogo v skladu z diferencialno enačbo po klasični shemi. Pri izračunu prehodnih procesov v kompleksnem vezju se sistem "m" diferencialnih enačb sestavi po Kirchhoffovih zakonih za diagram vezja po preklopu. Ker so koreni karakteristične enačbe skupni vsem spremenljivkam, se rešitev sistema diferencialnih enačb izvede glede na poljubno spremenljivko (opcijsko). Kot rezultat rešitve dobimo nehomogeno diferencialno enačbo z eno spremenljivko. Sestavite karakteristično enačbo v skladu z dobljeno diferencialno enačbo in določite njene korene.
Primer. Sestavite značilno enačbo in določite njene korene za spremenljivke v diagramu na sliki. 59.1. Parametri elementov so podani v splošni obliki.
Sistem diferencialnih enačb po Kirchhoffovih zakonih:
Rešimo sistem enačb za spremenljivko i3, posledično dobimo nehomogeno diferencialno enačbo:
Drugi način sestavljanja karakteristične enačbe je enačenje glavne determinante Kirchhoffovega sistema enačb za spremenljivke prostih komponent na nič.
Naj ima prosta komponenta poljubnega toka obliko iksv = Аkept, potem:
Sistem enačb za proste komponente dobimo iz Kirchhoffovega sistema diferencialnih enačb tako, da odvode spremenljivk nadomestimo s faktorjem p, integrale pa z 1/p. Za obravnavani primer ima sistem enačb za proste komponente obliko:
Karakteristična enačba in njen koren:
Tretji način za sestavljanje karakteristične enačbe (inženiring) je enačenje upora vhodnega operaterja vezja na nič glede na katero koli njegovo vejo.
Operaterski upor elementa dobimo iz njegovega kompleksnega upora s preprosto zamenjavo faktorja jω s p
Za zadevni primer:
Tretja metoda je najenostavnejša in najbolj ekonomična, zato se najpogosteje uporablja pri izračunu prehodnih procesov v električnih tokokrogih.
Koreni karakteristične enačbe označujejo prosti prehodni proces v tokokrogu brez virov energije. Ta proces poteka z izgubami energije in zato sčasoma propade. Iz tega sledi, da morajo biti koreni karakteristične enačbe negativni ali imeti negativen realni del.
V splošnem primeru sta vrstni red diferencialne enačbe, ki opisuje prehodni proces v tokokrogu, in posledično stopnja karakteristične enačbe ter število njenih korenin enaka številu neodvisnih začetnih pogojev oz. neodvisne naprave za shranjevanje energije (tuljave L in kondenzatorji C). Če shema vezja vsebuje vzporedno vezane kondenzatorje C1, C2,... ali zaporedno vezane tuljave L1, L2,..., jih je treba pri izračunu prehodnih procesov nadomestiti z enim enakovrednim elementom SE = C1 + C2+... ali LE = L1 + L2+...
Tako lahko splošno obliko rešitve za katero koli spremenljivko pri izračunu prehodnega procesa sestavimo samo iz analize diagrama vezja, brez sestavljanja in reševanja sistema diferencialnih enačb.
Za zgoraj obravnavani primer.
Opredelitev. Karakteristična enačba linearnega operatorja f je enačba oblike , kjer je λ poljubno realno število, A je matrika linearnega operatorja, E je identitetna matrika istega reda.
Polinom klical karakteristični polinom matriko A (linearni operator f). V matrični obliki ima karakteristična enačba naslednjo obliko:
oz
.
Posledično, če karakteristični polinom enačimo z nič, dobimo enačbo stopnje n, kjer je λ neznanka, dobimo vrednosti njenih korenin - značilne številke te matrike. Karakteristični koreni igrajo pomembno vlogo na mnogih področjih matematike. Razmislimo o eni od aplikacij karakterističnih korenov - zelo pomembnem orodju pri študiju linearnih prostorov, pa tudi pri reševanju številnih uporabnih problemov linearne algebre.
Množica vseh korenov karakteristične enačbe se imenuje spekter operatorja f(vsak koren je obravnavan z množico, ki jo ima v karakteristični enačbi).
Primer. Poiščite značilne korenine matrike.
Ustvarimo matrico
Če karakteristični polinom izenačimo z nič, dobimo kvadratno enačbo
Potem sta korena enačbe enaka 
.
Opredelitev. Naj bo f linearni operator prostora in naj bo nek ničelni vektor, za katerega velja enakost
kje je realno število. Potem se vektor imenuje lastni vektor operatorja, matrika njegovega operatorja pa lastna vrednost ali lastna vrednost transformacije. V tem primeru pravimo, da se lastni vektor nanaša na lastno vrednost.
Lastni vektorji igrajo pomembno vlogo tako v matematiki sami kot v njenih aplikacijah. Na primer resonanca, pri kateri lastne frekvence nihanja sistema sovpadajo s frekvenco nihanja zunanjih sil. V matematiki so lastni vektorji uporabni pri reševanju sistemov diferencialnih enačb.
Izrek. Če ima linearni operator f v bazi matriko A (prva baza) in matriko B v bazi (druga baza), potem velja enakost: .
Posledično se pri prehodu na novo osnovo karakteristični polinom linearnega operatorja ne spremeni.
◌ Če je T prehodna matrika iz prve baze v drugo, potem . Nato transformiramo desno stran enakosti ●
Izrek. Da bi bilo število λ 0 iz polja P lastna vrednost vektorja prostora L n nad P, je nujno in dovolj, da je število λ 0 karakteristični koren operatorja f.
Doc. JAZ. Nujnost. Pustiti λ 0 lastna vrednost operatorja f, nato v Ln obstaja lastni vektor, tako da .
Pustiti 
je torej njegova koordinatna premica v neki bazi
Po drugi strani, ker , kjer je torej matrika linearnega operatorja v dani bazi
Če izenačimo desni strani (1) in (2), dobimo:
(3)
Enakosti (3) pomenijo, da numerični vektor s koordinatami 
je rešitev naslednjega sistema enačb (4).
(4)
Vektor je različen od nič (ker je svoj), zato ima sistem (4) različno rešitev, zato je njegova determinanta 0.
(5)
zato je transpozibilna determinanta enaka 0.
(6)
torej λ 0 – koren karakteristične enačbe.
II. Ustreznost. Pustiti λ 0
– značilni koren operatorja v neki osnovi 
. Dokažimo to λ 0
je lastna vrednost operatorja A.
Res, če λ 0 je karakteristični koren, potem bo izpolnjena enakost (6) in s tem enakost (5), kar bo pomenilo, da ima sistem (4) rešitve, ki niso nič.
Izberimo neko neničelno rešitev sistema (4): numerični vektor 
. Potem so izpolnjene enakosti (3).
Oglejmo si vektor in zanj bo izpolnjena enakost (2) in na podlagi formule velja enakost (1), kjer je matrika operatorja v bazi IN. To implicira enakost, kar pomeni, da je vektor lastni vektor operatorja, ki mu lastna vrednost ustreza λ 0 . To je bilo treba dokazati. Izrek je dokazan.
Komentiraj. Da bi našli lastne vrednosti operatorja, je potrebno sestaviti in rešiti enačbo (5). Če želite najti lastne vektorje operatorja, morate ustvariti sistem enačb (4) in poiskati temeljni niz rešitev tega sistema.
Za nadzor pravilnosti izračuna lastnih vrednosti (lahko so sovpadajoče ali zapletene) se uporabljata dve dejstvi:
1) 
, kjer je zadnja vsota matrike sledi vsota diagonalnih elementov.
2) 
.
Primer. Poiščite lastne vrednosti in lastne vektorje 
.
Z enačenjem na nič dobimo . .
3) . , 
.
Naj bo prosta spremenljivka, potem dobimo vektor 
.
telovadba. Preverite vektor.
.
Karakteristična enačba je sestavljena za vezje po preklopu. Pridobite ga lahko na naslednje načine:
- neposredno na podlagi diferencialne enačbe oblike (2) (glej predavanje št. 24), t.j. z izključitvijo iz sistema enačb, ki opisujejo elektromagnetno stanje vezja na podlagi prvega in drugega Kirchhoffovega zakona, vseh neznanih količin razen ene, v povezavi s katero je zapisana enačba (2);
- z uporabo izraza za vhodno impedanco tokokroga sinusnega toka;
- na podlagi izražanja glavne determinante.
Po prvi metodi je bila v prejšnjem predavanju pridobljena diferencialna enačba napetosti na kondenzatorju za serijsko R-L-C vezje, na podlagi katere je zapisana karakteristična enačba.
Upoštevati je treba, da ker je linearno vezje zajeto z enim samim prehodnim procesom, so koreni karakteristične enačbe skupni vsem prostim komponentam napetosti in tokov vej vezja, katerih parametri so vključeni v karakteristično enačbo. Zato lahko po prvi metodi sestavljanja karakteristične enačbe katero koli spremenljivko izberemo kot spremenljivko, glede na katero je zapisana.
Oglejmo si uporabo druge in tretje metode sestavljanja karakteristične enačbe z uporabo primera vezja na sl. 1.
Sestavljanje karakteristične enačbe z uporabo metode vhodnega upora je naslednje:
zabeleži se vhodni upor izmeničnega tokokroga;
jw se nadomesti z operatorjem p;
dobljeni izraz je enak nič.
Enačba
sovpada z značilnim.
Poudariti je treba, da lahko vhodni upor zapišemo glede na prelomno točko katere koli veje vezja. V tem primeru se aktivno dvopolno omrežje nadomesti s pasivnim po analogiji z metodo ekvivalentnega generatorja. Ta metoda sestavljanja karakteristične enačbe predpostavlja odsotnost magnetno sklopljenih vej v vezju; če obstajajo, je potrebno izvesti njihovo predhodno razvezavo.
Za vezje na sl. 1 glede na izvorne terminale
.
Če jw zamenjamo s p in dobljeni izraz enačimo z nič, zapišemo
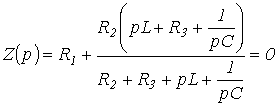
| . | (1) |
Pri sestavljanju karakteristične enačbe na podlagi izraza glavne determinante je število algebraičnih enačb, na podlagi katerih je zapisana, enako številu neznanih komponent prostega toka. Algebraizacija izvirnega sistema integro-diferencialnih enačb, sestavljenega na primer na podlagi Kirchhoffovih zakonov ali metode konturnih tokov, se izvede z zamenjavo simbolov diferenciacije oziroma integracije z množenjem in deljenjem z operatorjem str. Karakteristično enačbo dobimo tako, da zapisano determinanto enačimo z nič. Ker izraz za glavno determinanto ni odvisen od desnih strani sistema nehomogenih enačb, ga lahko sestavimo na podlagi sistema enačb, zapisanih za skupne tokove.
Za vezje na sl. 1 algebraizirani sistem enačb, ki temelji na metodi tokovne zanke, ima obliko
Od tod izraz za glavno determinanto tega sistema
Če D enačimo z nič, dobimo rezultat, podoben (1).
Splošna metodologija za izračun prehodnih procesov po klasični metodi
Na splošno metodologija za izračun prehodnih procesov po klasični metodi vključuje naslednje korake:
Primeri izračuna prehodnih procesov po klasični metodi
1. Prehodni procesi v tokokrogu R-L, ko je priključen na vir napetosti
Takšni procesi potekajo na primer pri priključitvi elektromagnetov, transformatorjev, elektromotorjev itd. na vir energije.
Razmislimo o dveh primerih:
Glede na obravnavano metodo za tok v vezju na sl. 2 se lahko napiše
Karakteristična enačba
torej časovna konstanta 
.
torej
| . | (5) |
Če nadomestimo (4) in (5) v relacijo (3), zapišemo
.
Po prvem zakonu komutacije. Potem
,
Tako je tok v vezju med prehodnim procesom opisan z enačbo
,
in napetost na induktorju je podana z
.
Kvalitativni videz krivulj in ustreznih dobljenih rešitev je predstavljen na sliki 1. 3.
Za drugo vrsto vira se vsiljena komponenta izračuna s simbolno metodo:
,
Izraz proste komponente ni odvisen od vrste napetostnega vira. torej
.
Od takrat
Tako končno dobimo
| . | (6) |
Analiza dobljenega izraza (6) kaže:
Če je po velikosti pomembna, se prosta komponenta v polovici obdobja ne zmanjša bistveno. V tem primeru lahko največja vrednost prehodnega toka znatno preseže amplitudo stacionarnega toka. Kot je razvidno iz sl. 4, kjer
, se največji tok pojavi po približno . V meji pri.
Tako za linearno vezje največja vrednost prehodnega toka ne more preseči dvakratne amplitude prisilnega toka: .
Podobno velja za linearno vezje s kondenzatorjem: če je v trenutku preklopa vsiljena napetost enaka njeni amplitudni vrednosti in je časovna konstanta vezja dovolj velika, potem po približno polovici obdobja napetost na kondenzatorju doseže največjo vrednost. , ki ne sme presegati dvakratne amplitude vsiljene napetosti: 
.
2. Prehodni procesi pri odklopu induktorja od vira napajanja
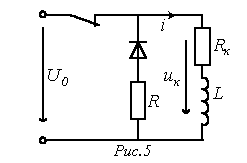
Ko je ključ odprt v vezju na sl. 5 prisilna komponenta toka skozi induktor.
Karakteristična enačba
,
kje 
in 
.
Po prvem zakonu komutacije
.
Tako je izraz za prehodni tok
in napetost na induktorju
 .
|
(7) |
Analiza (7) kaže, da lahko pri odpiranju tokokrogov, ki vsebujejo induktivne elemente, pride do velikih prenapetosti, ki lahko brez posebnih ukrepov poškodujejo opremo. Res, kdaj 
Napetostni modul na induktorju v trenutku preklopa bo večkrat višji od napetosti vira: . V odsotnosti dušilnega upora R se na odpiralne kontakte ključa uporabi določena napetost, zaradi česar se med njimi pojavi lok.
3. Polnjenje in praznjenje kondenzatorja
Ko se ključ premakne v položaj 1 (glej sliko 6), se začne postopek polnjenja kondenzatorja:
.
Prisilna komponenta napetosti na kondenzatorju.
Iz karakteristične enačbe
koren je določen 
. Od tod časovna konstanta.
