Relația dintre coordonatele carteziene și cele polare. Coordonate polare

Numărul este sunat raza polară puncte sau prima coordonată polară. Distanța nu poate fi negativă, deci raza polară a oricărui punct este . Prima coordonată polară se notează și cu litera greacă („rho”), dar m-am obișnuit cu versiunea latină, iar pe viitor o voi folosi.

Numărul este sunat unghi polar punct dat sau a doua coordonată polară. Unghiul polar este schimbat în mod standard în (așa-numitul valorile principale ale unghiului). Cu toate acestea, este destul de acceptabil să folosiți intervalul și, în unele cazuri, există o nevoie directă de a lua în considerare toate valorile unghiurilor de la zero la „plus infinit”. Recomand, de altfel, să te obișnuiești cu măsura în radian a unghiului, deoarece nu se consideră comme il faut să operezi cu grade în matematică superioară.

Cuplul este sunat coordonate polare puncte . De ușor de găsit și semnificațiile lor specifice. Tangenta unui unghi ascuțit al unui triunghi dreptunghic este raportul dintre catetul opus și catetul adiacent: prin urmare, unghiul însuși: . Conform teoremei lui Pitagora, pătratul ipotenuzei este egal cu suma pătratelor catetelor: deci, raza polară:

În acest fel, .

Un pinguin este bun, dar o turmă este mai bună:



Colțuri orientate negativ pentru orice eventualitate, am marcat cu săgeți, deodată unul dintre cititori nu știa încă de această orientare. Dacă doriți, puteți „înșuruba” 1 tură la fiecare dintre ele (rad. sau 360 de grade) și deveniți, apropo, confortabil valorile tabelului:

Dar dezavantajul acestor colțuri orientate „tradițional” este că sunt prea mult (mai mult de 180 de grade) „răsucite” în sens invers acelor de ceasornic. Prevăd întrebarea: „de ce lipsă și de ce avem nevoie de unghiuri negative?” În matematică se pun în valoare căile cele mai scurte și mai raționale. Ei bine, din punct de vedere al fizicii, sensul de rotație este adesea de o importanță fundamentală - fiecare dintre noi a încercat să deschidă ușa trăgând mânerul în direcția greșită =)

Ordinea și tehnica de construire a punctelor în coordonate polare

Imaginile frumoase sunt frumoase, dar construirea unui sistem de coordonate polare este o sarcină destul de minuțioasă. Dificultățile nu apar cu punctele ale căror unghiuri polare sunt , în exemplul nostru acestea sunt punctele ; valorile care sunt multipli de 45 de grade, de asemenea, nu cauzează prea multe probleme: . Dar cum să construiești corect și competent, să zicem, un punct?

Veți avea nevoie de o bucată de hârtie în carouri, un creion și următoarele instrumente de desen: riglă, busolă, raportor. În cazuri extreme, te poți descurca cu o singură riglă sau chiar... fără ea! Citiți mai departe și veți obține încă o dovadă că această țară este invincibilă =)

Exemplul 1

Construiți un punct în sistemul de coordonate polare.

În primul rând, trebuie să aflați măsura gradului unghiului. Dacă unghiul este necunoscut sau aveți îndoieli, atunci este întotdeauna mai bine să îl utilizați masa sau formula generală pentru transformarea radianilor în grade. Deci unghiul nostru este (sau ).

Să desenăm un sistem de coordonate polare (vezi începutul lecției) și să luăm un raportor. Nu va fi dificil pentru proprietarii unui instrument rotund să marcheze 240 de grade, dar cu o probabilitate mare veți avea o versiune semicirculară a dispozitivului pe mâini. Problema absenței complete a raportorului în prezența unei imprimante și a foarfecelor rezolvate prin aci.

Există două moduri: întoarceți foaia și marcați 120 de grade sau „înșurubați” o jumătate de tură și luați în considerare unghiul opus. Să alegem metoda pentru adulți și să facem un semn de 60 de grade:



Fie un raportor pitic, fie o cușcă gigantică =) Cu toate acestea, pentru a măsura unghiul, scara nu este importantă.

Desenăm cu un creion o linie dreaptă subțire care trece prin stâlp și se face semnul:



Ne-am dat seama unghiul, următorul pas este raza polară. Luăm o busolă și prin domnitor am stabilit soluția sa la 3 unități, cel mai adesea, acestea sunt, desigur, centimetri:

Acum punem cu grijă acul pe stâlp, iar cu o mișcare de rotație facem o crestătură mică (roșu). Punctul dorit este construit:



Puteți face fără busolă atașând o riglă direct pe linia construită și măsurând 3 centimetri. Dar, după cum vom vedea mai târziu, în sarcini de construcţie în sistemul de coordonate polare o situație tipică este atunci când trebuie să marcați două sau mai multe puncte cu aceeași rază polară, deci este mai eficient să întăriți metalul. În special, în desenul nostru, rotind piciorul busolei cu 180 de grade, este ușor să faceți o a doua crestătură și să construiți un punct simetric față de stâlp. Pe el, să elaborăm materialul următorului paragraf:

Relația dintre sistemele de coordonate dreptunghiulare și polare

Evident a te alatura la sistemul de coordonate polare al grilei de coordonate „normale” și desenați un punct pe desen:

Această conexiune este întotdeauna utilă de reținut atunci când desenați coordonatele polare. Deși, vrând-nevrând, se sugerează fără prea multe indicii.

Să stabilim relația dintre coordonatele polare și carteziene folosind exemplul unui punct specific. Să considerăm un triunghi dreptunghic, în care ipotenuza este egală cu raza polară: , iar catetele sunt coordonatele „x” și „joc” ale punctului din sistemul de coordonate carteziene: .

Sinusul unui unghi ascuțit este raportul dintre catetul opus și ipotenuză:

Cosinusul unui unghi ascuțit este raportul dintre catetul adiacent și ipotenuză:

În același timp, au repetat definițiile sinusului, cosinusului (și puțin mai devreme tangentei) din programul clasei a IX-a a unei școli generale.

Vă rugăm să adăugați în cartea dvs. de referință formule de lucru care exprimă coordonatele carteziene ale unui punct în termeni de coordonatele sale polare - va trebui să ne ocupăm de ele de mai multe ori și data viitoare chiar acum =)

Să găsim coordonatele unui punct într-un sistem de coordonate dreptunghiular:

În acest fel:

Formulele rezultate deschid o altă lacună în problema construcției, când poți să faci fără raportor: mai întâi găsim coordonatele carteziene ale punctului (desigur, pe proiect), apoi găsim mental locul potrivit pe desen. și notează acest punct. Pe stadiu final trasăm o linie dreaptă subțire care trece prin punctul construit și prin pol. Ca urmare, se pare că unghiul a fost măsurat cu un raportor.

E amuzant că elevii absolut disperați se pot descurca chiar și fără riglă, folosind în schimb marginea netedă a unui manual, caiet sau caiet de note - până la urmă, producătorii de caiete s-au ocupat de metrica, 1 celulă = 5 milimetri.

Toate acestea mi-au adus aminte de o anecdotă binecunoscută în care piloți ingenioși au trasat un curs de-a lungul pachetului Belomor \u003d) Deși, glumele sunt glume, iar anecdota nu este atât de departe de realitate, îmi amintesc că pe unul dintre zborurile interne peste tot. Federația Rusă, toate dispozitivele de navigație au eșuat în linie, iar echipajul a aterizat cu succes placa folosind un pahar obișnuit cu apă, care a arătat unghiul de înclinare al aeronavei față de sol. Și pista de aterizare - iată-o, vizibilă de pe parbriz.

Folosind teorema lui Pitagora citată la începutul lecției, se obține ușor formule inverse: , deci:

Unghiul „phi” în sine este exprimat standard prin arc tangente - exact la fel ca argument de număr complex cu toate ciudateniile ei.

De asemenea, este recomandabil să plasați al doilea grup de formule în bagajele de referință.

După o analiză detaliată a zborurilor cu puncte individuale, să trecem la continuarea firească a subiectului:

Ecuația dreaptă în coordonate polare

În esență, ecuația unei linii într-un sistem de coordonate polare este funcția razei polare a unghiului polar (argument). În acest caz, se ia în considerare unghiul polar în radiani(!) și continuu ia valori de la la (uneori ar trebui să fie considerat la infinit, sau într-o serie de probleme pentru comoditate de la până la ). Fiecare valoare a unghiului „phi”, care este inclusă în domeniu funcţie, corespunde unei singure valori a razei polare.

Funcția polară poate fi comparată cu un fel de radar - atunci când un fascicul de lumină care emană de la stâlp se rotește în sens invers acelor de ceasornic și „detectează” (trasează) o linie.

Un exemplu comun de curbă polară este Spirala arhimediană. Figura următoare o arată primul rând– când raza polară care urmează unghiului polar ia valori de la 0 la: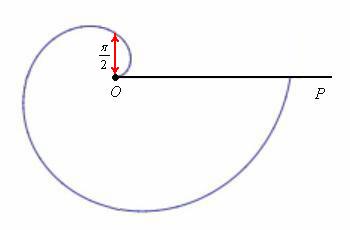

În plus, traversând axa polară în punctul , spirala va continua să se deruleze, la infinit departe de pol. Dar astfel de cazuri sunt destul de rare în practică; o situație mai tipică, când la toate revoluțiile ulterioare „mergem pe aceeași linie”, care se obține în intervalul .

În primul exemplu, întâlnim și conceptul domenii Funcția polară: deoarece raza polară este nenegativă, unghiurile negative nu pot fi luate în considerare aici.

! Notă : în unele cazuri este obișnuit să se folosească coordonate polare generalizate, unde raza poate fi negativă și vom studia pe scurt această abordare puțin mai târziu

Pe lângă spirala lui Arhimede, există multe alte curbe binecunoscute, dar, după cum se spune, nu vei fi plin de artă, așa că am luat exemple care sunt foarte comune în sarcini practice reale.

În primul rând, cele mai simple ecuații și cele mai simple linii:

O ecuație de formă specifică ieșirea de la pol Ray. Într-adevăr, gândiți-vă dacă valoarea unghiului mereu(oricare ar fi „er”) în mod constant, atunci care este linia?

Notă : în sistemul de coordonate polar generalizat, această ecuație definește o linie dreaptă care trece prin pol

Ecuația formei determină ... ghici prima dată - dacă pentru oricine raza colțului „phi” rămâne constantă? De fapt, această definiție cercuri centrat la polul razei .

De exemplu, . Pentru claritate, să găsim ecuația acestei linii într-un sistem de coordonate dreptunghiular. Folosind formula obținută în paragraful anterior, vom efectua înlocuirea:

Să pătram ambele părți:

– ecuația cercului centrat la originea coordonatelor de raza 2, care urma să fie verificată.

De la crearea și lansarea articolului pe dependența liniară și independența liniară a vectorilor Am primit mai multe scrisori de la vizitatorii site-ului care au pus o întrebare în spirit: „iată un simplu și convenabil sistem dreptunghiular coordonate, de ce avem nevoie de un alt caz afin oblic?”. Răspunsul este simplu: matematica caută să îmbrățișeze totul și totul! În plus, în această sau acea situație, comoditatea este importantă - după cum puteți vedea, este mult mai profitabil să lucrați cu un cerc în coordonate polare datorită simplității extreme a ecuației.

Și uneori modelul matematic anticipează descoperiri științifice. Deci, la un moment dat, rectorul Universității din Kazan N.I. Lobaciovski riguros dovedit, printr-un punct arbitrar al planului se poate desena număr infinit de linii paralel cu cel dat. Drept urmare, a fost defăimat de întreaga lume științifică, dar... nimeni nu a putut infirma acest fapt. Abia după un secol bun, astronomii au aflat că lumina în spațiu se propagă pe traiectorii curbe, unde geometria non-euclidiană a lui Lobachevsky, dezvoltată oficial de el cu mult înainte de această descoperire, începe să funcționeze. Se presupune că aceasta este o proprietate a spațiului în sine, a cărei curbură este invizibilă pentru noi datorită distanțelor mici (după standardele astronomice).

Luați în considerare sarcini de construcție mai semnificative:

Exemplul 2

construi o linie

Soluţie: prima găsi domeniu. Deoarece raza polară este nenegativă, inegalitatea trebuie să se mențină. Vă puteți aminti regulile școlare pentru rezolvarea inegalităților trigonometrice, dar în cazuri simple ca acesta, vă sfătuiesc o metodă mai rapidă și mai vizuală de rezolvare:

Imaginați-vă un complot cosinus. Dacă nu a reușit încă să fie depus în memorie, atunci găsește-l pe pagină Grafice ale funcțiilor elementare. Ce ne spune inegalitatea? Ne spune că graficul cosinus ar trebui să fie localizat nu mai puțin axa absciselor. Și asta se întâmplă pe un segment. Și, în consecință, intervalul nu se potrivește.

Astfel, domeniul funcției noastre este: , adică graficul este situat în dreapta polului (după terminologia sistemului cartezian, în semiplanul drept).

În coordonatele polare, există adesea o idee vagă despre ce linie definește această sau acea ecuație, așa că pentru a o construi, trebuie să găsiți punctele care îi aparțin - și cu cât mai multe, cu atât mai bine. De obicei limitat la o duzină sau două (sau chiar mai puțin). Cel mai simplu mod, desigur, este să luați valorile unghiurilor tabelare. Pentru o mai mare claritate, voi „face” o întoarcere la valorile negative:

Datorită parității cosinusului valorile pozitive corespunzătoare pot fi omise din nou:

Să descriem sistemul de coordonate polare și să lăsăm deoparte punctele găsite, în timp ce este convenabil să lăsăm deoparte aceleași valori ale lui „er” la un moment dat, făcând serif-uri împerecheate cu o busolă conform tehnologiei discutate mai sus:

În principiu, linia este clar trasată, dar pentru a confirma absolut presupunerea, să găsim ecuația acesteia în sistemul de coordonate carteziene. Puteți aplica formule nou derivate , dar vă voi spune despre un truc mai complicat. Înmulțim artificial ambele părți ale ecuației cu „er”: și folosim formule de tranziție mai compacte:

Selectând pătratul complet, aducem ecuația dreptei într-o formă recunoscută:

– ecuația cercului centrat în punctul , raza 2.

Deoarece, în funcție de condiție, era pur și simplu necesar să se finalizeze construcția și asta este, conectăm fără probleme punctele găsite cu o linie:

Gata. E în regulă dacă iese puțin neuniform, nu trebuia să știi că a fost un cerc ;-)

De ce nu am luat în considerare valorile unghiurilor în afara intervalului? Răspunsul este simplu: nu are sens. Având în vedere periodicitatea funcției, așteptăm o alergare nesfârșită de-a lungul cercului construit.

Este ușor să efectuați o analiză simplă și să ajungeți la concluzia că ecuația formei definește un cerc de diametru cu un centru în punctul . Figurat vorbind, toate astfel de cercuri „stau” pe axa polară și trec în mod necesar prin pol. Dacă , atunci compania veselă se va deplasa la stânga - la continuarea axei polare (gândește-te de ce).

O problemă similară pentru o soluție independentă:

Exemplul 3

Desenați o dreaptă și găsiți ecuația acesteia într-un sistem de coordonate dreptunghiular.

Sistematizăm procedura de rezolvare a problemei:

În primul rând, găsim domeniul funcției, pentru aceasta este convenabil să ne uităm sinusoid pentru a înțelege imediat unde este sinusul nenegativ.

În a doua etapă, calculăm coordonatele polare ale punctelor folosind valori tabelare ale unghiurilor; să analizeze dacă este posibil să se reducă numărul de calcule?

În al treilea pas, lăsăm deoparte punctele din sistemul de coordonate polare și le conectăm cu atenție printr-o linie.

Și, în sfârșit, găsim ecuația dreptei în sistemul de coordonate carteziene.

Exemplu de soluție la sfârșitul lecției.

Detaliem algoritmul general și tehnica de construcție în coordonate polare
și accelerează semnificativîn a doua parte a prelegerii, dar înainte de asta, să ne familiarizăm cu încă o linie comună:

trandafir polar

Foarte corect, vorbim despre o floare cu petale:

Exemplul 4

Trasează linii date de ecuații în coordonate polare

Există două abordări pentru construirea unui trandafir polar. În primul rând, să mergem de-a lungul pistei moletate, presupunând că raza polară nu poate fi negativă:

Soluţie:

a) Aflați domeniul funcției:

O astfel de inegalitate trigonometrică este, de asemenea, ușor de rezolvat grafic: din materialele articolului Transformări ale diagramei geometrice Se știe că dacă argumentul funcției este dublat, atunci graficul său se va micșora la axa y de 2 ori. Vă rugăm să găsiți graficul funcției în primul exemplu al lecției specificate. Unde se află această sinusoidă deasupra axei x? La intervale . Prin urmare, segmentele corespunzătoare satisfac inegalitatea și domeniu functia noastra: .

În general, soluția inegalităților luate în considerare este unirea unui număr infinit de segmente, dar, din nou, ne interesează doar o singură perioadă.

Poate că unii cititori vor găsi metoda analitică de găsire a domeniului definiției mai ușoară, o voi numi condiționat „tăierea unei plăcinte rotunde”. Vom tăia în părți egaleși, în primul rând, găsiți limitele primei piese. Argumentăm după cum urmează: sinusul este nenegativ, când argumentul lui variază de la 0 la rad. inclusiv. În exemplul nostru: . Împărțind toate părțile inegalității duble la 2, obținem intervalul necesar:

Acum începem secvenţial să „tăiem bucăţi egale de 90 de grade” în sens invers acelor de ceasornic:

- segmentul găsit, desigur, este inclus în zona de definire;

– intervalul următor – nu este inclus;

- următorul segment - intră;

- și, în sfârșit, intervalul - nu este inclus.

La fel ca mușețelul - „iubește, nu iubește, iubește, nu iubește” =) Cu diferența că asta nu este ghicitor. Da, se dovedește doar un fel de dragoste în chineză...

Asa de, iar linia reprezintă un trandafir cu două petale identice. Este foarte posibil să desenați un desen schematic, dar este foarte de dorit să găsiți și să marcați corect vârfurile petalelor. Vârfurile corespund punctele mijlocii ale segmentelor domeniului de definire, in care acest exemplu au coordonate unghiulare evidente . în care lungimea petalei sunteți:

Iată rezultatul natural al unui grădinar grijuliu:

Trebuie remarcat faptul că lungimea petalei este ușor de văzut imediat din ecuație - deoarece sinusul este limitat: , atunci valoarea maximă a „er” cu siguranță nu va depăși două.

b) Să construim dreapta dată de ecuație. Evident, lungimea petalei acestui trandafir este și ea de două, dar, în primul rând, ne interesează domeniul definiției. Aplicăm metoda analitică de „feliere”: sinusul este nenegativ atunci când argumentul său este în intervalul de la zero la „pi” inclusiv, în acest caz: . Împărțim toate părțile inegalității la 3 și obținem primul interval:

Apoi, începem să „tăiem plăcinta în bucăți” conform rad. (60 de grade):
– segmentul va intra în zona de definire;
– interval – nu va intra;
- segment - va intra;
– interval – nu va intra;
- segment - va intra;
- interval - nu va intra.

Procesul a fost finalizat cu succes la marca de 360 ​​de grade.

Deci domeniul de aplicare este: .

Acțiunile desfășurate integral sau parțial sunt ușor de realizat mental.

Constructie. Dacă în paragraful anterior totul a mers bine cu unghiuri drepte și unghiuri de 45 de grade, atunci aici trebuie să mânuiești puțin. Sa gasim vârfurile petalelor. Lungimea lor a fost vizibilă încă de la începutul sarcinii, rămâne de calculat coordonatele unghiulare, care sunt egale cu punctele de mijloc ale segmentelor domeniului de definiție:

Vă rugăm să rețineți că între vârfurile petalelor trebuie neapărat să obțineți goluri egale, în acest caz 120 de grade.

Este de dorit să marcați desenul în sectoare de 60 de grade (delimitate de linii verzi) și să desenați direcțiile vârfurilor petalelor (linii gri). Este convenabil să marcați vârfurile în sine cu ajutorul unei busole - o dată măsurați distanța de 2 unități și aplicați trei crestături în direcțiile desenate la 30, 150 și 270 de grade:

Gata. Înțeleg că sarcina este supărătoare, dar dacă vrei să aranjezi totul într-un mod inteligent, va trebui să petreci timp.

Formulăm formula generală: o ecuație de forma , este un număr natural), definește un trandafir cu petale polare a cărui lungime a petalei este de .

De exemplu, ecuația specifică un quatrefoil cu o lungime a petalei de 5 unități, ecuația - un trandafir cu 5 petale cu o lungime a petalei de 3 unități. etc.

Fie dat pe plan un sistem de coordonate carteziene dreptunghiulare Oxy. Setul de puncte din plan, ale căror coordonate x și y satisfac egalitatea în care F (x, y) este o funcție a două variabile, se numește curbă plată sau linie plată; egalitatea (*) însăși se numește ecuația dreptei (curbei) dată. De exemplu, egalitatea x - y \u003d 0 este ecuația unei linii drepte - bisectoarea primului și a celui de-al treilea unghi de coordonate (Fig. 7). Egalitatea x2 + y2 - 1 = 0 este ecuația unui cerc de rază unitară centrat la origine (Fig. 8). Se consideră un polinom de gradul doi în două variabile x și y: Ecuație Curbe de ordinul doi. Proprietățile elipsei. Ce este Hyperbole. va fi numită ecuația de ordinul doi (curba) a liniilor. Dacă liniile de ordinul întâi sunt tocmai linii drepte și numai ele, atunci setul de curbe de ordinul al doilea este vizibil mai divers. Prin urmare, este firesc să prefațăm studiul ecuației generale a unei curbe de ordinul doi prin studierea unor cazuri particulare, dar importante. O elipsă este o curbă a cărei ecuație într-un sistem de coordonate cartezian dreptunghiular Oxy are forma Sistemul de coordonate Oxy, în care ecuația unei elipse are forma (1), se numește canonică (pentru o elipsă dată); ecuația (1) însăși se numește ecuația canonică a elipsei. Cercul este un caz special al unei elipse (când a = b). Aceasta face posibilă determinarea formei elipsei într-un mod simplu: elipsa (1) se obține din cercul (2) prin contracția sa uniformă1) a firului Ox (cu coeficientul t), adică. prin înlocuirea în ecuaţia x2 + y2 = a2 coordonatele y cu (Fig. 9). Proprietățile unei elipse 1. Elipsa (1) este conținută într-un dreptunghi * Este ușor de verificat acest lucru notând că dacă punctul M (x, y) aparține elipsei (1), atunci (Fig. 10) Punctele se numesc vârfurile elipsei. 2. Axele de coordonate Ox și Oy ale sistemului canonic sunt axele de simetrie ale elipsei, iar originea O este centrul acesteia de simetrie. Aceasta înseamnă că dacă punctul Mq(x0, yQ) aparține elipsei, atunci îi aparțin și punctele (~xo, yo), (~x0, -yo) și (hou-yo) (Fig. 11). 3. Dacă elipsa nu este un cerc, atunci axele de coordonate ale sistemului canonic sunt singurele axe de simetrie. Fie c = Va2 - b2. Este clar că punctele (-c, 0) și (c, 0) sunt numite focare ale elipsei, respectiv, stânga și dreapta; 2s - distanta focala. 4. O elipsă este o mulțime de puncte, suma distanțelor cărora de la două puncte date (focurile elipsei) este constantă (egală cu un număr dat). !> Comprimarea uniformă a cercului pe axa x cu un coeficient k > 0 este o transformare care duce un punct arbitrar M(x, y) al cercului în punctul M" ) ). Mai întâi, fie M(x, y) un punct arbitrar al elipsei Să calculăm distanța cc de la focarele elipsei (Fig. 12). Avem Înlocuirea y cu expresia lui după transformări simple, obținem că ultima egalitate rezultă din faptul că. În mod similar, găsim că este ușor să verificăm că curbele sunt de ordinul doi. Proprietățile elipsei. Ce este Hyperbole. Dovada că punctele cu proprietatea indicată aparțin unei elipse a fost efectuată mai devreme (vezi secțiunea „Cele mai simple probleme de geometrie analitică” din Introducere, problema 2). Numărul se numește excentricitatea elipsei (I). Este clar că. Excentricitatea cercului este zero. Liniile drepte se numesc directrice ale elipsei. Fiecare elipsă are două directrice - stânga și dreapta (Fig. 13 Elipsa este un set de puncte ale planului, raportul dintre distanțe de la un punct dat (focalizarea elipsei) și la o linie dreaptă dată (a aceleiași nume ca focar al directricei elipsei) este constantă (egal cu excentricitatea elipsei). 4 Fie mai întâi L/(x, y) este un punct arbitrar al elipsei (1).Calculăm distanțele de la purtător la focarul drept și la directricea dreaptă (Fig. 14).Avem, respectiv, De unde obținem cu ușurință pe cel cerut. 0) și dreapta x = J (c = oe).Se ia un punct arbitrar M(x , y) și se calculează distanțele de la acesta până la punctul ales (c, 0) - yj(- și până la dreapta aleasă - Se cere ca Atunci Ridicăm ambele părți ale ultimei relații la pătrat și, punând și ținând cont de egalitatea c = ae, după transformări simple obținem Astfel, punctul M(x, r/) se află pe elipsa (1). O hiperbolă este o curbă a cărei ecuație într-un sistem de coordonate dreptunghiular Oxy are forma în care coordonatorul de sistem , în care ecuația hiperbolei are forma (1), se numește canonică (pentru hiperbola dată); ecuația (1) însăși se numește ecuația canonică a unei hiperbole. Proprietățile hiperbolei 1. Hiperbola (1) se află în afara benzii |3| h Aceasta rezultă din faptul că, dacă punctul M(x, y) se află pe o hiperbolă, atunci curbele sunt de ordinul doi. Proprietățile elipsei. Ce este Hyperbole. și deci punctele (±a, 0) se numesc vârfurile hiperbolei. 2. Hiperbola (1) se află în unghiurile verticale formate de dreptele y = ±\x şi conţinând punctele axei x (Fig. 16). Figura 15 4 Din inegalitate Să luăm două puncte din primul trimestru: punctul hiperbolei (1) și punctul asimptotei sale f-jf = 0 cu aceeași abscisă x, respectiv - și să calculăm distanța dintre ele. Avem Înmulțirea și împărțirea expresiei rezultate cu suma x + Vx2 - a2 și trecând apoi la limita la, obținem a: + Vx2 - a2 Astfel, se stabilește următorul fapt. 4. Dacă punctul curent al asimptotei se îndepărtează la infinit de origine, i.e. |x| -» + oo, apoi pe hiperbolă se poate indica punctul corespunzător acesteia astfel încât distanța dintre ele să tinde spre zero (Fig. 18). Este adevărat și invers. 5. Dacă punctul curent M(x, y) al hiperbolei se îndepărtează la infinit de punctul 0(0, 0), adică. x2 + y2 oo, atunci distanța sa până la una dintre liniile drepte tinde spre zero. 6. Axele sistemului de coordonate canonice sunt axele de simetrie ale hiperbolei, iar originea coordonatelor este centrul său de simetrie (Fig. 19). Axele de coordonate ale sistemului canonic sunt singurele axe de simetrie ale hiperbolei. Punem c = y/a2 + b2. Este clar că c > 0. Punctele (-c, 0) și (c, 0) se numesc focarele hiperbolei, 2c este distanța focală. 7. O hiperbolă este o mulțime de puncte, valoarea absolută a diferenței de distanțe de la care la două puncte date (focare de hiperbolă) este constantă (egală cu un număr dat). Dovada acestei proprietăți se realizează în același mod ca și proba proprietății 4 a elipsei. Să arătăm, de exemplu, că fiecare punct al hiperbolei are proprietatea indicată. Dacă M(x, y) este un punct al hiperbolei (1), atunci distanțele de la aceasta la focare sunt, respectiv, egale (Fig. 20). Deoarece ~ > 1, este ușor de calculat de aici că și, prin urmare, Numărul se numește excentricitatea hiperbolei (1). Este clar că c > 1. Liniile se numesc directrice ale hiperbolei (Fig. 21). Fiecare hiperbolă are o ydvedirectrix - stânga și dreapta. Aproape în același mod ca și pentru elipsă, se demonstrează următorul fapt. O hiperbolă este un set de puncte, raportul dintre distanțele de la un punct dat (focalizarea hiperbolei) și linia dreaptă dată (directricea cu același nume cu focarul) este constant (egal cu excentricitatea lui hiperbola) (Fig. 22). O hiperbolă se numește hiperbolă conjugată (1). Dispunerea reciprocă a hiperbolelor (1) și (2) este prezentată în fig. 23.

Ecuaţie numiți o expresie formată din două părți, care sunt separate printr-un semn „egal” în așa fel încât în ​​fiecare parte să apară combinații algebrice de numere și litere.

Astfel, expresia y=2, în ciuda simplității sale, este o ecuație. LA plan cartezian mulţimea de puncte ale căror coordonate satisfac această ecuaţie formează o dreaptă paralelă cu axa y care trece prin punctul (0, 2). Ecuația y=x este o dreaptă formată din puncte a căror abscisă și ordonată sunt aceleași. Astfel, vorbim despre bisectoarea primului și al treilea cadran, adică o linie dreaptă care împarte unghiul drept în două unghiuri identice de 45 °. Trebuie să înțelegeți că ecuația y=x este identică cu ecuația y-x=0, totuși, precum și ecuația x-y=0.

Ori de câte ori variabilele x sau y nu sunt ridicate la o putere într-o ecuație (sau mai bine, când puterea este egală cu unu), această ecuație este linie dreaptă pe plan. Iată mai multe exemple de ecuații în linie dreaptă:
y=3x-2, 6y-8x=0, -2y=6x+1.

Desenați o linie grafic foarte simplu: pentru a-l desena, trebuie să cunoști doar două dintre punctele sale. Cel mai convenabil este să determinați acele două puncte în care linia se intersectează. Acest lucru se face în felul următor

Să presupunem că vrem să trasăm o linie dreaptă y=3x-6. În punctul în care linia intersectează axa x, ordonata ar trebui să fie 0. Astfel, echivalând y cu 0, obținem 0=3x-6, sau echivalent, 3x=6. Deci x=6/3=2.

Echivalând x cu 0 în același mod, obținem y=-6. În acest fel, puncte de intersecție linia dorită cu axe de coordonate sunt: ​​(2, 0) și (0, -6). Acum putem deja să tragem o linie dreaptă.

De asemenea, se pot reprezenta prin ecuații figuri mai complexe: cercuri, elipse, orice fel de suprafețe conice. Este clar că ecuațiile care descriu figuri complexe vor fi mai complexe decât ecuațiile de linii. De exemplu, ecuația $x^2+y^2=9$ descrie un cerc centrat la origine și raza 3. Și formula $\frac(x^2)(4)+\frac(y^2)(9)=1$ este ecuația elipsei centrat la origine și semiaxele 2 și 3.

În plus, pentru a indica părți ale avionului, puteți utiliza inegalităților. De exemplu, mulțimea punctelor x și y care îndeplinesc condițiile $0 \leq x \leq 2, 0 \leq y \leq 1$ se află în interiorul unui dreptunghi cu vârfuri (0,0), (2,0), (2, 1) și (0,1).

Intrebarea 1. Explicați cum sunt determinate coordonatele unui punct.
Răspuns. Să desenăm două drepte reciproc perpendiculare x și y pe planul prin punctul O - axele de coordonate (Fig. 170). Axa x (de obicei orizontală) se numește axa x, iar axa y este axa y. Punctul de intersecție O - originea coordonatelor - fiecare dintre axe este împărțită în două semiaxe. Să fim de acord să numim unul dintre ele pozitiv, marcând-o cu o săgeată, iar celălalt negativ.

Fiecărui punct A al planului asociem o pereche de numere - coordonatele punctului - abscisa (x) și ordonata (y) conform acestei reguli.
Prin punctul A trasăm o dreaptă paralelă cu axa y (Fig. 171). Acesta va traversa axa x la un punct A x . Abscisa punctului A o vom numi numărul x, a cărui valoare absolută este egală cu distanța de la punctul O la punctul A x . Acest număr va fi pozitiv dacă Ax aparține semiaxei pozitive și negativ dacă Ax aparține semiaxei negative. Dacă punctul A se află pe axa y, atunci setăm x egal cu zero.

Ordenata (y) a punctului A este definită în mod similar. Desenați o linie dreaptă prin punctul A paralel cu axa x (vezi Fig. 171). Acesta va intersecta axa y la un punct A y . Vom numi ordonata punctului A numărul y, a cărui valoare absolută este egală cu distanța de la punctul O la punctul A y . Acest număr va fi pozitiv dacă A y aparține semiaxei pozitive și negativ dacă A y aparține semiaxei negative. Dacă punctul A se află pe axa x, atunci setăm y egal cu zero.
Vom scrie coordonatele punctului între paranteze lângă denumirea literei punctului, de exemplu: A (x; y) (abscisa în primul rând, ordonată în al doilea).

Intrebarea 2. Care sunt semnele coordonatelor unui punct dacă acesta aparține primului (al doilea, al treilea, al patrulea) trimestru?
Răspuns. Axele de coordonate împart planul în patru părți - sferturi: I, II, III, IV (Fig. 172). Într-un sfert, semnele ambelor coordonate sunt păstrate și au semnificații.

Dacă punctul aparține primului trimestru, atunci abscisa și ordonatele sale vor fi pozitive.
Dacă punctul aparține celui de-al doilea trimestru, atunci abscisa lui va fi negativă, iar ordonata va fi pozitivă.
Dacă punctul aparține celui de-al treilea trimestru, atunci abscisa și ordonatele sale vor fi negative.
Dacă punctul aparține celui de-al patrulea trimestru, atunci abscisa sa va fi pozitivă, iar ordonata va fi negativă.

Întrebarea 3. Care sunt abscisele punctelor de pe axa y?
Care sunt ordonatele punctelor de pe axa x?
Care sunt coordonatele originii?
Răspuns. Punctele axei x (abscise) au ordonate zero (y = 0), iar punctele axei y (axa y) au abscise zero (x = 0).
Dacă orice punct se află pe axa y, atunci abscisa acestui punct este zero.
Dacă orice punct se află pe axa x, atunci ordonata acestui punct este zero.
La origine, abscisa și ordonata sunt zero.

Întrebarea 4. Deduceți formule pentru coordonatele mijlocului segmentului.
Răspuns. Fie A (x 1 ; y 1) și B (x 2 ;y 2) două puncte arbitrare și C (x; y) punctul de mijloc al segmentului AB. Aflați coordonatele x, y ale punctului C.
Să luăm mai întâi în considerare cazul în care segmentul AB nu este paralel cu axa y, i.e. \(x_1 \neq x_2\). Să trasăm drepte prin punctele A, B, C, paralele cu axa y (Fig. 173). Ei vor traversa axa x în punctele A1 (\(x_1\); 0), B1 (\(x_2\); 0), C (\(x\); 0). Conform teoremei Thales, punctul \(C_1\) va fi punctul de mijloc al segmentului \(A_1B_1\).

Deoarece punctul \(C_1\) este punctul mijlociu al segmentului \(A_1B_1\), atunci \(A_1C_1 = B_1C_1\), și deci \(|x – x_1| = |x – x_2|\). Rezultă că fie \(x - x_1 = -(x - x_2)\). Prima egalitate este imposibilă deoarece \(x_1 \neq x_2\). Prin urmare, al doilea este adevărat. Și de aici vine formula

\(x = \frac(x_1 + x_2)(2)\).

Dacă \(x_1 = x_2\), adică. segmentul AB este paralel cu axa y, atunci toate cele trei puncte \(A_1, B_1, C_1\) au aceeași abscisă. Prin urmare, formula rămâne adevărată și în acest caz.
În mod similar se găsește ordonata punctului C. Prin punctele A, B, C sunt trasate linii paralele cu axa x. Se pare că formula

\(x = \frac(y_1 + y_2)(2)\).

Întrebarea 5. Deduceți o formulă pentru distanța dintre puncte.
Răspuns. Să fie date două puncte pe planul xy: \(A_1\) cu coordonatele \(x_1, y_1\) și \(A_2\) cu coordonatele \(x_2, y_2\). Să exprimăm distanța dintre punctele \(A_2\) și \(A_2\) în termeni de coordonatele acestor puncte.
Luați în considerare mai întâi cazul în care \(x_1 \neq x_2\) și \(y_1 \neq y_2\). Să trasăm drepte prin punctele \(A_1\) și \(A_2\), paralele cu axele de coordonate, și notăm cu A punctul de intersecție a acestora (Fig. 174). Distanța dintre punctele \(A\) și \(A_1\) este \(|y_1 – y_2|\), iar distanța dintre punctele \(A\) și \(A_2\) este \(|x_1 – x_2| \) . Aplicând teorema lui Pitagora triunghiului dreptunghic \(AA_1A_2\), obținem:

\(d^2 = (x_1 - x_2)^2+ (y_1 - y_2)^2\), (*)

unde d este distanța dintre punctele \(A_1\) și \(A\).

Deși formula (*) pentru distanța dintre puncte a fost derivată de noi sub ipoteza \(x_1 \neq x_2\), \(y_1 \neq y_2\), aceasta rămâne adevărată și în alte cazuri. Într-adevăr, dacă \(x_1 = x_2\), \(y_1 \neq y_2\), atunci d este egal cu \(|y_2 - y_2|\). Formula (*) dă același rezultat. Cazul când \(x_1 \neq x_2, y_1 = y_2\) este considerat în mod similar. Pentru \(x_1 = x_2, y_1 = y_2\) punctele \(A_1\) și \(A_2\) coincid, iar formula (*) d = 0.

Întrebarea 6. Care este ecuația unei figuri în coordonate carteziene?
Răspuns. Ecuația unei figuri în coordonate carteziene pe un plan este o ecuație cu două necunoscute x și y, care este îndeplinită de coordonatele oricărui punct al figurii. Și invers: orice două numere care satisfac această ecuație sunt coordonatele unui punct al figurii.

Întrebarea 7. Deduceți ecuația cercului.
Răspuns. Să compunem ecuația unui cerc centrat în punctul A O (a; b) și raza R (Fig. 175). Luați un punct arbitrar A (x; y) pe cerc. Distanța de la acesta la centrul A O este \((x - a)^2 + (y - b)^2\). Astfel, coordonatele x, y ale fiecărui punct A al cercului satisfac ecuația

\((x - a)^2 + (y - b)^2 = R^2\). (*)

În schimb, orice punct A, ale cărui coordonate satisfac ecuația (*), aparține cercului, deoarece distanța de la acesta până la punctul A O este egală cu R. Rezultă că ecuația (*) este într-adevăr ecuația unui cerc cu centrul A O și raza R. Rețineți că, dacă centrul cercului este originea, atunci ecuația cercului este:

\(x^2 + y^2 = R^2\).

Întrebarea 8. Demonstrați că linia dreaptă în coordonate carteziene are o ecuație de forma ax + by + c = 0.
Răspuns. Să demonstrăm că orice dreaptă în coordonatele carteziene x, y are o ecuație de forma

ax + by + c = 0, (*)

unde a, b, c sunt unele numere.
Fie h o dreaptă arbitrară pe planul xy. Să desenăm o dreaptă perpendiculară pe linia dreaptă h și să trasăm pe ea din punctul de intersecție al lui C cu dreapta h segmente egale CA 1 și CA 2 (Fig. 176).

Fie a 1 , b 1 coordonatele punctului A 1 şi a 2 , b 2 coordonatele punctului A 2 . După cum știm, orice punct A (x; y) al dreptei h este echidistant de punctele A 1 și A 2 . Prin urmare, coordonatele sale satisfac ecuația

\((x - a_1)^2 + (y - b_1)^2 = (x - a_2)^2 + (y - b_2)^2\). (**)

În schimb, dacă coordonatele x și y ale unui punct satisfac ecuația (**), atunci acest punct este echidistant de punctele A 1 și A 2 și, prin urmare, aparține dreptei h. Astfel, ecuația (**) este o ecuație a dreptei h. Dacă deschidem parantezele din această ecuație și mutăm toți termenii ecuației în partea stângă, atunci aceasta va lua forma:

\(2(a_2 - a_1)x + 2(b_2 - b_1)y + (a_1^2 + b^2_1 - a^2_2 - b^2_2) = 0.\)

Notând \(2(a_2 - a_1) = a\), \(2(b_2 - b_1) = b\), \(a^2_1 + b^2_1 - a^2_2 - b^2_2 = c\), vom obțineți ecuația (*). Afirmația a fost dovedită.

Întrebarea 9. Cum se găsesc coordonatele punctului de intersecție a două drepte dacă sunt date ecuațiile acestor drepte?
Răspuns. Să fie date ecuațiile a două drepte:

ax + by + c = 0,

a 1 x + b 1 y + c 1 = 0.

Găsiți coordonatele punctului lor de intersecție.
Deoarece punctul de intersecție (x; y) aparține fiecăreia dintre drepte, coordonatele sale satisfac atât prima cât și a doua ecuație. Prin urmare, coordonatele punctului de intersecție sunt soluția sistemului de ecuații care definesc dreptele. Luați în considerare un exemplu.
Fie ecuațiile acestor drepte:

3x - y + 2 = 0,

5x - 2y + 1 = 0.

Rezolvând acest sistem de ecuații, găsim x = -3, y = -7. Punct de intersecție a liniilor (-3; -7).

Întrebarea 10. Cum se află linia dreaptă dacă coeficientul a = 0 (b = 0; c = 0) în ecuația sa?
Răspuns. Să aflăm cum este situată linia dreaptă în raport cu axele de coordonate dacă ecuația ei ax + by + c = 0 are una sau alta formă particulară.
1. a = 0, b \(\neq\) 0. În acest caz, ecuația unei drepte poate fi rescrisă astfel:

\(y = -\frac(c)(b)\).

Astfel, toate punctele dreptei au aceeași ordonată (\(-\frac(c)(b)\)); prin urmare, linia dreaptă este paralelă cu axa x (Fig. 177, a). În special, dacă c = 0, atunci linia coincide cu axa x.
2. b = 0, a \(\neq\) 0. Acest caz este tratat în mod similar. Linia dreaptă este paralelă cu axa y (Fig. 177, b) și coincide cu aceasta dacă c = 0.

3. c \u003d 0. Linia dreaptă trece prin origine, deoarece coordonatele sale (0; 0) satisfac ecuația dreptei (Fig. 177, c).

Întrebarea 11. Care este panta unei drepte și care este semnificația ei geometrică?
Răspuns. Dacă în ecuația generală a dreptei ax + by + c = 0 coeficientul la y nu este egal cu zero, atunci această ecuație poate fi rezolvată în raport cu y. Primim:

\(y = -\frac(a)(b)x - \frac(c)(b)\).

Sau, notând \(-\frac(a)(b) = k\), \(-\frac(c)(b) = l\), obținem:

Să aflăm semnificația geometrică a coeficientului k în această ecuație.
Luați două puncte de pe dreapta A (x 1 ; y 1), B(x 2 ; y 2) (x 1)< x 2). Их координаты удовлетворяют уравнению прямой:

y 1 = kx 1 + l, y 2 = kx 2 + l.

Scăzând aceste egalități termen cu termen, obținem y 2 - y 1 = k (x 2 - x 1). De aici

\(k = \frac(y_2 - y_1)(x_2 - x_1)\).

În cazul prezentat în Figura 178, a, \(\frac(y_2 - y_1)(x_2 - x_1) = tg \alpha\).
În cazul prezentat în Figura 178b, \(\frac(y_2 - y_1)(x_2 - x_1) = -tg \alpha\).

Astfel, coeficientul k în ecuația unei drepte, până la un semn, este egal cu tangentei unghiului ascuțit pe care îl formează dreapta cu axa x. Coeficientul k din ecuația unei drepte se numește panta dreptei.

Întrebarea 12. Demonstrați că graficul unei funcții liniare este o dreaptă.
Răspuns. Fie y = ax + b o funcție liniară dată. Să demonstrăm că graficul său este o linie.
Pentru această funcție, dacă x = 0, atunci y = b, dacă x = 1, atunci y = a + b. Prin urmare, graficul funcției conține punctele (0; b) și (1; a + b). Să scriem ecuația unei drepte care trece prin aceste puncte. După cum știm, arată așa:

Deoarece punctele indicate ale graficului se află pe o dreaptă, coordonatele lor satisfac ecuația unei linii drepte:

\(b = k \cdot 0 + l\),

\(a + b = k \cdot 1 + l\).

De aici găsim l = b, k = a. Deci linia noastră are ecuația

Aceasta înseamnă că toate punctele graficului satisfac ecuația unei linii drepte. Adică, graficul unei funcții liniare este o linie dreaptă.

Întrebarea 13.În ce condiție o dreaptă și un cerc nu se intersectează, se intersectează în două puncte, se ating?
Răspuns. Fie R raza cercului și d distanța de la centrul cercului la linia dreaptă. Să luăm ca origine a coordonatelor centrul cercului, iar drepta perpendiculară pe cea dată ca axa x (Fig. 179). Atunci ecuația cercului va fi \(x^2 + y^2 = R^2\), iar ecuația dreptei x = d.
Pentru ca o dreaptă și un cerc să se intersecteze, este necesar ca sistemul a două ecuații

\(x^2 + y^2 = R^2\), x = d

avea o solutie. Și invers: orice soluție a acestui sistem oferă coordonatele x, y ale punctului de intersecție al dreptei cu cercul. Rezolvând sistemul nostru, obținem:

x = d, \(y = \pm\sqrt(R^2 – d^2)\).

Din expresia pentru y se poate observa că sistemul are două soluții, i.e. un cerc şi o dreaptă au două puncte de intersecţie dacă R> d (Fig. 179, a).
Sistemul are o soluție dacă R = d (Fig. 179, b). În acest caz, linia și cercul se ating.
Sistemul nu are soluție, adică. linia și cercul nu se intersectează dacă R< d (рис. 179, в).

Întrebarea 14. Definiți sinus, cosinus și tangentă pentru orice unghi de la 0° la 180°.
Răspuns. Să luăm un cerc pe planul xy cu centrul la origine și raza R (Fig. 180). Să trasăm unghiul \(\alpha\) din axa x pozitivă în semiplanul superior (semiplanul unde y > 0). Fie x și y coordonatele punctului A. Valorile \(\sin \alpha\), \(\cos \alpha\) și \(tg \alpha\) pentru un unghi ascuțit \(\alpha\) sunt exprimate în coordonatele punctului A și anume:

\(\cos \alpha = \frac(x)(R)\), \(\sin \alpha = \frac(y)(R)\), \(tg \alpha = \frac(y)(x) \).

Să definim acum valorile \(\sin \alpha\), \(\cos \alpha\) și \(tg \alpha\) prin aceste formule pentru orice unghi \(\alpha\). (Pentru \(tg \alpha\) unghiul \(\alpha = 90°\) este exclus.)
Cu această definiție, \(\sin 90° = 1\), \(\cos 90° = 0\), \(\sin 180° = 0\), \(\cos 180° = -1\), \ ( tan 180° = 0\).
Presupunând că razele coincidente formează un unghi de 0°, vom avea: \(\sin 0° = 0\), \(\cos 0° = 1\), \(tg 0° = 0\).

Întrebarea 15. Demonstrați că pentru orice unghi \(\alpha\), \(0°< \alpha < 180°\),
\(\sin (180° - \alpha) = \sin \alpha\), \(\cos (180° - \alpha) = -\cos \alpha\),
Răspuns. Să demonstrăm că pentru orice unghi \(\alpha\), \(0°< \alpha < 180°\), \(\sin (180° - \alpha) = \sin \alpha\), \(\cos (180° - \alpha) = -\cos \alpha\). Для угла \(\alpha \neq 90°\) \(tg (180° - \alpha) = -tg \alpha\).

Într-adevăr, triunghiurile OAB și OA 1 > B 1 sunt egale în ipotenuză și unghi ascuțit (Fig. 181). Din egalitatea triunghiurilor rezultă că AB = A 1 B 1 , adică. y = y 1 ; OB \u003d OB 1, prin urmare, x \u003d -x 1. De aceea

\(\sin (180° - \alpha) = \frac(y_1)(R) = \frac(y)(R) = \sin \alpha\),

\(\cos (180° - \alpha) = \frac(x_1)(R) = \frac(-x)(R) = -\cos \alpha\).

Împărțind termen cu termen egalitatea \(\sin (180° - \alpha) = \sin \alpha\) la egalitatea \(\cos (180° - \alpha) = -\cos \alpha\), obținem:

\(tg (180° - \alpha) = -tg \alpha\).

Q.E.D.

Geometrie analitică– ramură a matematicii în care problemele geometrice se rezolvă cu ajutorul algebrei pe baza metodei coordonatelor. Apariția metodei coordonatelor este strâns legată de dezvoltarea rapidă a astronomiei, mecanicii și tehnologiei în secolul al XVII-lea. O prezentare clară și exhaustivă a acestei metode și a fundamentelor geometriei analitice a fost făcută de P. Descartes în „Geometria” sa (1637). Ideile principale ale metodei erau cunoscute și de contemporanul său P. Fermat. Dezvoltarea ulterioară a geometriei analitice este asociată cu lucrările lui G. Leibniz , I. Newton şi mai ales L. Euler.

Importanța geometriei analitice constă în faptul că această direcție stabilește relația dintre curbele geometrice și ecuațiile algebrice. Această relație face posibilă transformarea problemelor de geometrie în probleme de ecuații algebrice și invers. În ultima vreme, în timpul creșterii rapide a tehnologiei informatice, concepte precum animația pe computer și implementarea automată a designului par a fi fenomene de zi cu zi. Aceste aplicații se bazează pe geometria analitică 3D.

Conceptele de bază ale geometriei analitice sunt cele mai simple imagini geometrice (puncte, linii, plane, curbe și suprafețe de ordinul doi. Metodele geometriei analitice sunt aplicabile figurilor din plan și suprafețelor din spațiul tridimensional și, de asemenea, permit generalizări naturale la spaţii de dimensiuni mai mari.Vom pleca de la geometria analitică la plan.

Problema principală a geometriei analitice constă în studiul figurilor geometrice folosind relaţiile dintre coordonatele punctelor din care se formează aceste figuri. Orice figură poate fi considerată ca un set de puncte care satisfac o anumită condiție geometrică. Această condiție poate fi scrisă ca o ecuație algebrică care raportează coordonatele Xși y fiecare punct al figurii. Esența metodei geometriei analitice este de a studia proprietățile unei figuri cu ajutorul ecuației corespunzătoare, studiate cu ajutorul algebrei. Această metodă permite stabilirea unor fapte geometrice într-un mod sistematic, spre deosebire de geometria „sintetică” tradițională, în care trebuia să inventeze metode de demonstrare pentru fiecare caz individual.

Esența metodei coordonatelor este următoarea. Luați în considerare, de exemplu, în avion p două drepte reciproc perpendiculare Bouși OU. Aceste linii drepte cu direcțiile pozitive indicate pe ele, originea O și unitatea de scară aleasă formează Sistemul de coordonate carteziene Ohu la suprafata. Direct Bouși OU se numesc axa absciselor, respectiv axa ordonatelor. Poziția oricărui punct Mîn avion în raport cu acest sistem Ohu poate fi definită după cum urmează. Lăsa Mxși Ale mele- proiecții M pe Bouși OU, si numerele Xși y- cantități segmente dirijate OMxși Omu. Conceptul de segment direcționat înseamnă că cantitatea X segment OMx, de exemplu, este egală cu lungimea acestui segment, luată cu semnul plus, dacă direcția este de la O la Mx coincide cu direcția pe o linie dreaptă Bou, iar cu semnul minus altfel. Numerele Xși la se numesc coordonatele dreptunghiulare carteziene ale punctului Mîn sistem Ohu. Acestea sunt de obicei denumite abscisă și, respectiv, ordonată punctului. M. Pentru a desemna un punct M cu abscisă X si ordonata la utilizați simbolul M(X y). Este clar că coordonatele punctului M determina pozitia acestuia fata de sistem Ohu.

Lasă în avion p cu un sistem de coordonate carteziene dat Ohu dat o linie L. Folosind conceptul de coordonate punct, putem introduce conceptul de ecuație a unei drepte date L referitor la sistem Ohu ca relaţii de formă F(X y) = 0, care este satisfăcut de coordonate Xși la orice punct M, situat pe Lși nu satisface coordonatele fiecărui punct pe care nu se află L. Dacă, de exemplu, linia L este un cerc cu raza R cu centrat la origine O, apoi ecuația x2+ y2 - R2 = 0 va fi ecuația cercului luat în considerare, așa cum se poate vedea făcând referire la orez. 2 . Dacă punct M se află pe cerc, apoi după teorema lui Pitagora pentru un triunghi OMMx se dovedește x2 + y2- R2 = 0. Dacă punctul nu se află pe cerc, atunci, evident, x2 + y2- R2¹ 0. Deci liniile Lîn avion, puteți compara ecuația acestuia F(X y) = 0 raportat la sistemul de coordonate Ohu.

Ideea principală a metodei coordonatelor pe un plan este că proprietățile geometrice ale unei linii L se află studiind prin mijloace analitice şi algebrice proprietăţile ecuaţiei F(X y) = 0 această linie. De exemplu, aplicăm metoda coordonatelor pentru a afla numărul de puncte de intersecție a unui cerc C cu rază Rși această linie dreaptă LA(orez. 3 ).

Fie originea sistemului de coordonate Ohu este în centrul cercului, iar axa Bouîndreptată perpendicular pe o dreaptă LA. Din moment ce linia dreaptă LA perpendicular pe ax Bou, atunci abscisa oricărui punct al acestei drepte este egală cu o constantă A. Astfel, ecuația unei linii drepte LA are forma x-a= 0. Coordonate ( X y) punctele de intersecție ale cercului DIN, a cărui ecuație are forma x2 + y2- R2= 0 și direct LA satisface simultan ecuaţiile

Obțineți textul integral

x2 + y2 - R2 = 0, X-a = 0, (1)

adică sunt o soluție pentru sistemul (1). În consecință, întrebarea geometrică despre numărul de puncte de intersecție ale dreptei și cercului se reduce la întrebarea analitică despre numărul de soluții ale sistemului algebric (1). Rezolvând acest sistem, obținem x \u003d a, y \u003d ±. Deci, cercul și linia se pot intersecta în două puncte ( R2 > a2) (acest caz este prezentat în orez. 3 ), poate avea un punct comun ( R2 = a2) (în acest caz, linia dreaptă LA atinge cercul C) și nu au puncte comune ( R2< a2 ) (în acest caz, linia dreaptă LA se află în afara cercului C).

În geometria analitică pe plan, sunt studiate sistematic așa-numitele drepte algebrice de ordinul întâi și al doilea. Aceste drepte în coordonate dreptunghiulare carteziene sunt determinate, respectiv, de ecuații algebrice de gradul I și II. Liniile de ordinul întâi sunt drepte și invers, fiecare linie dreaptă este determinată de o ecuație algebrică de gradul I Axe + By+ С = 0. Liniile de ordinul doi sunt determinate de ecuații de formă Ax2 + Bxy + Cy2 + Dx + Ey + F= 0. Principala metodă de studiere și clasificare a acestor drepte este de a selecta un astfel de sistem de coordonate carteziene dreptunghiulare în care ecuația dreptei are cea mai simplă formă, apoi studiați această ecuație simplă. Se poate dovedi că în acest fel ecuația oricărei drepte reale de ordinul doi poate fi redusă la una dintre următoarele forme cele mai simple:

http://pandia.ru/text/78/223/images/image004_102.gif" width="91 height=52" height="52">, , , .

Prima dintre aceste ecuații definește o elipsă, a doua o hiperbolă, a treia o parabolă, iar ultimele două o pereche de linii (în intersectare, paralele sau îmbinate).

Deci, între mulțimea de drepte de pe plan și mulțimea de ecuații cu două necunoscute există o corespondență unu-la-unu.

În geometria analitică în spațiu se folosește și metoda coordonatelor. În acest caz, coordonatele dreptunghiulare carteziene. X, lași z(abscisa, ordonata si aplicate) puncte M sunt introduse în totală analogie cu cazul plan (vezi . orez).

http://pandia.ru/text/78/223/images/image009_54.gif" width="70" height="22"> relativ la sistemul de coordonate Oxyz.(De exemplu, ecuația pentru o sferă cu rază R centrat la origine are forma x2 + y2 + z2 - R2= 0.) În acest caz, proprietățile geometrice ale suprafeței S sunt clarificate prin studierea proprietăților ecuației acestei suprafețe prin mijloace analitice și algebrice. linia Lîn spațiu este definită ca linia de intersecție a două suprafețe S1și S1.În cazul în care un F1(x, y, z) = 0 și F2(x, y, z) = 0 - ecuații de suprafață S 1 și S 2, atunci perechea acestor ecuații, considerate împreună, este ecuația dreptei L. De exemplu, drept Lîn spațiu poate fi considerată drept o linie de intersecție a două plane. Deoarece planul în spațiu este determinat de o ecuație de formă Topor + Prin + Cz + D= 0, atunci o pereche de ecuații de această formă, considerate împreună, este o ecuație a unei drepte L. Astfel, metoda coordonatelor poate fi folosită și pentru a studia liniile în spațiu. În geometria analitică în spațiu, așa-numita suprafețe algebrice de ordinul întâi și al doilea. Se dovedește că numai planurile sunt suprafețe algebrice de ordinul întâi. Suprafețe de ordinul doi sunt definite prin ecuații de forma:

Ax2 + By2 + Cz2+ Dxy + Eyz+Fxz + Gx + Ei bine + Mz + N = 0.

Metoda principală de studiere și clasificare a acestor suprafețe este de a selecta un astfel de sistem de coordonate dreptunghiular carteziene în care ecuația de suprafață are cea mai simplă formă, apoi de a studia această ecuație simplă. Cele mai importante suprafețe reale de ordinul doi sunt:

- elipsoid;

- hiperboloid cu o singură foaie;

- hiperboloid cu două foi;

Paraboloid eliptic;

Paraboloid hiperbolic.

Cele mai importante suprafețe enumerate de ordinul doi sunt adesea întâlnite în diverse probleme de mecanică, fizica stării solide, fizica teoretică și inginerie. Deci, în studiul tensiunilor care apar într-un corp solid, ei folosesc conceptul așa-numitului: elipsoid de stres. În diferite structuri de inginerie, se folosesc structuri sub formă de hiperboloizi și paraboloizi.

I. Geometrie analitică în plan

1. Axă și segment de axă. Coordonate pe o linie dreaptă

Se numește o linie cu direcție pozitivă axă . În desene, direcția pozitivă a axei este indicată printr-o săgeată. Un segment al unei axe delimitat de câteva puncte Ași B, se numește segment dirijat , dacă se spune care dintre aceste puncte este considerat începutul segmentului, care este sfârșitul. Segment direcționat cu originea într-un punct Ași se termină într-un punct B indicat prin simbol. Dimensiunea segmentului dirijat lungimea sa se numește, luată cu semnul plus dacă direcția segmentului (adică direcția de la început până la sfârșit) coincide cu direcția pozitivă a axei și cu semnul minus dacă această direcție este opusă direcției pozitive. direcția axei. Valoare segment http://pandia.ru/text/78/223/images/image017_31.gif" width="30" height="19">. Din cele spuse, este clar că valoarea segmentului, în contrast la lungimea sa, este un număr relativ. În mod evident, lungimea unui segment este modulul mărimii sale, prin urmare, în conformitate cu modul algebric de a desemna modulul unui număr, vom folosi simbolul /text/categ/nauka.php" class="myButtonNauka"> Obțineți textul complet pentru a indica lungimea unui segment

Să fie dată niște axe A. Hai să luăm câteva pe scară largă segment de linie ca unitate de măsură pentru lungimi și marcați pe această literă dreaptă O un moment dat. Astfel, pe linie dreaptă A vor fi introduse sistem de coordonate .

Coordonarea oricărui punct M Drept A(în sistemul de coordonate stabilit) se numește număr X, egal cu dimensiunea segmentului OM:

Punct O numită origine; propria sa coordonată este zero. În viitor, simbolul M(X) înseamnă că punctul M are o coordonată X.

Dacă și sunt două puncte arbitrare pe o dreaptă A, apoi formula

exprimă valoare segment de linie, formulă

o exprimă lungime.

2. Coordonate carteziene dreptunghiulare pe plan

D Sistemul de coordonate carteziene este definită prin setarea unei unități liniare pentru măsurarea lungimii și a două axe reciproc perpendiculare, numerotate într-o anumită ordine.

Se numește punctul de intersecție al axelor origine și topoarele în sine - coordona topoare . Prima dintre axa de coordonate este numită axa x , al doilea - axa y .

Originea coordonatelor este indicată prin literă O, abscisă - simbol Oh, axa y - simbol OU.

Coordonatele unui punct arbitrar M dintr-un sistem dat sunt numerele

Când se calculează folosind această formulă, aria se va dovedi pozitivă dacă vârfurile sunt ocolite în ordinea numerotării lor în sens invers acelor de ceasornic și negativă în cazul opus.

Aceasta, în special, implică condiția pentru amplasarea a trei puncte pe o singură linie dreaptă:

http://pandia.ru/text/78/223/images/image067_8.gif" width="77" height="25 src=">, , , ,… este

http://pandia.ru/text/78/223/images/image074_6.gif" width="54" height="25"> și .

7. Ecuația unei drepte ca loc al punctelor

Ecuația dreptei este ecuația http://pandia.ru/text/78/223/images/image078_6.gif" width="14" height="21"> cu coordonatele ( A, B). Coeficient DAR cu o variabilă X este prima coordonată a vectorului normal al dreptei și coeficientul LA cu o variabilă la este a doua coordonată a vectorului normal al dreptei.

Rețineți că dacă două ecuații generale http://pandia.ru/text/78/223/images/image079_6.gif" width="123" height="23 src="> definesc aceeași linie, atunci există un număr t, că egalitățile sunt adevărate

A1=A·t, B1=Bt, C1=Ct.

Luați în considerare modul în care se află linia dreaptă în raport cu sistemul de coordonate, în funcție de valorile coeficienților A Bși DIN ecuația generală a unei linii drepte:

a) la C \u003d 0 - linia dreaptă trece prin origine;

b) la B = 0 - linia dreaptă este paralelă cu axa Oy;

c) la A \u003d 0 - o linie dreaptă este paralelă cu axa Ox;

d) la B \u003d C \u003d 0 Ax \u003d 0, x \u003d 0 - axa Oy;

e) la A = C = 0 By = 0, y = 0 - axa Ox.

Să transferăm parametrul în ecuația generală DINîn partea dreaptă și împărțiți ambele părți ale ecuației la - DIN. Ecuația va lua forma

http://pandia.ru/text/78/223/images/image084_6.gif" width="67" height="32">, .

http://pandia.ru/text/78/223/images/image087_7.gif" width="14" height="17 src=">.gif" width="53" height="23"> . Evident, un punct M(X y) se află pe linia specificată dacă și numai dacă vectorii http://pandia.ru/text/78/223/images/image089_6.gif" width="53" height="23"> sunt coliniari, adică atunci când coordonatele acestor vectori sunt proporționale:

Această ecuație se numește ecuația canonică a unei linii drepte.

Rețineți că în ecuația canonică, linia directă este unul dintre numitorii sau http://pandia.ru/text/78/223/images/image092_7.gif" width="11" height="23"> și nu poate fi egal cu zero, deoarece vectorul http://pandia.ru/text /78 /223/images/image094_6.gif" width="68" height="23"> poate fi înțeles ca , dispariția unuia dintre numitori înseamnă dispariția numărătorului corespunzător. Într-adevăr, dacă, de exemplu, , atunci, din moment ce , concluzionăm din egalitate că .

În concluzie, scriem ecuația unei drepte care trece prin două puncte date M1(x1, y1) și M2(x2, y2). Considerăm că punctele sunt diferite unele de altele..gif" width="127" height="51 src=">.

Aceasta este ecuația unei drepte care trece prin două puncte dintr-un plan, cu coordonatele date ( x1, y1), (x2, y2).

Ecuații parametrice ale unei linii drepte. Ecuațiile parametrice ale dreptei sunt obținute elementar din ecuația canonică. Scriem ecuația canonică sub forma

http://pandia.ru/text/78/223/images/image103_7.gif" width="81" height="25 src=">.gif" width="102" height="55 src=">.

Ecuațiile rezultate sunt ecuațiile parametrice necesare ale dreptei. Ecuațiile permit o interpretare mecanică clară. Dacă presupunem că parametrul t de data aceasta, atunci ecuațiile parametrice rezultate determină mișcarea unui punct de-a lungul unei drepte cu o viteză constantă.

Obțineți textul integral

Să dăm ca exemplu ecuația parametrică a unui cerc. Lăsa M(X y) este punctul curent al cercului centrat la origine și rază R.

http://pandia.ru/text/78/223/images/image108_6.gif" width="85" height="48 src=">.

Pentru a obține ecuația cercului în coordonate carteziene, excludem parametrul din sistemul de ecuații t. Pentru a face acest lucru, pătram fiecare ecuație a sistemului și le adăugăm:

http://pandia.ru/text/78/223/images/image110_6.gif" width="17" height="16">înclinarea liniei pe direcția pozitivă a axei Oh numit factor de pantă Drept și este de obicei notat prin literă k:

http://pandia.ru/text/78/223/images/image110_6.gif" width="17" height="16">=0, apoi k=0. Aceasta înseamnă că linia este paralelă cu axa Oh iar panta sa este zero.

Dacă , atunci nu are sens. Aceasta înseamnă că linia este perpendiculară pe axă Oh si nu are panta.

Coeficientul de pantă poate fi calculat dacă sunt cunoscute coordonatele oricăror două puncte ale acestei drepte: M1(x1, y1) și M(X y). Apoi

http://pandia.ru/text/78/223/images/image115_5.gif" width="148" height="27 src=">.

Dacă linia intersectează axa Oi la un moment dat ( 0 ,b), atunci ecuația ia forma

http://pandia.ru/text/78/223/images/image117_5.gif" width="89" height="25 src=">

Această ecuație se numește ecuația unei drepte cu pantă ; k denotă panta dreptei date și b- reprezintă valoarea segmentului interceptat de o dreaptă dată pe axă Oi pornind de la originea coordonatelor. Pentru a vedea acest lucru, este suficient să luăm în considerare sistemul de ecuații

http://pandia.ru/text/78/223/images/image120_4.gif" width="16" height="21 src=">- unghiul de înclinare al acestei perpendiculare pe axa Ox. Pentru a aduce generalul ecuația unei linii drepte Ah + By + C= 0 la forma normalizată, trebuie să înmulțiți toți membrii acesteia cu factorul de normalizare

,

luate cu semnul opus termenului liber C. Aceasta deoarece ecuaţia generală Ah+Wu+C=0 iar ecuația normalizată trebuie să definească aceeași linie dreaptă. Și în virtutea observației făcute în secțiunea „ecuația generală a unei linii drepte”, există un astfel de număr t, ce http://pandia.ru/text/78/223/images/image123_4.gif" width="84 height=21" height="21">,.Pătratând primele două egalități și apoi adunându-le, obținem , Unde

.

Rămâne să clarificăm care dintre semne să luăm în această formulă. Din moment ce sensul distanţei R este întotdeauna nenegativ, apoi din egalitate

rezultă că semnul t semnul opus DIN.

Distanţă d de la punctul (x; y) la linia dreaptă găsim dacă substituim coordonatele (x; y) în partea stângă a ecuației normale a dreptei în locul coordonatelor curente și luăm numărul rezultat în valoare absolută :

http://pandia.ru/text/78/223/images/image128_5.gif" width="112" height="47 src=">.

Condiția paralelismului a două drepte. Evident direct. și paralele între ele dacă k1 = k2 . Dacă dreptele sunt date de ecuaţiile generale A1x+B1y+C1=0și A2x+B2y+C2=0, apoi rescriindu-le sub formă

și , vedem asta , . Prin urmare, condiția liniilor paralele va lua forma

http://pandia.ru/text/78/223/images/image137_5.gif" width="25" height="47 src="> sau .

Condiția de perpendicularitate a două drepte. . Evident direct. și sunt perpendiculare între ele dacă unghiurile http://pandia.ru/text/78/223/images/image140_4.gif" width="20" height="23 src="> ale acestor linii pe axă Oh sunt legate prin raportul http://pandia.ru/text/78/223/images/image142_5.gif" width="41" height="19 src=">. Atunci sau . Dacă liniile sunt date prin ecuații generale A1x+B1y+C1=0și A2x+B2y+C2=0, ținând cont de faptul că , , obținem condiția de perpendicularitate a două drepte, exprimată în termeni de coeficienți ai ecuației generale a dreptei

http://pandia.ru/text/78/223/images/image146_4.gif" width="24" height="47 src="> sau .

Ecuația pachetului de linii. Ansamblul tuturor liniilor dintr-un plan care trec printr-un punct M(x0,y0) se numește mănunchi de linii drepte centrat M.

Lăsa A1x+B1y+C1=0și A2x+B2y+C2=0 sunt ecuațiile a două drepte care se intersectează într-un punct M, și sunt numere arbitrare care nu sunt egale cu zero în același timp. Apoi + http://pandia.ru/text/78/223/images/image152_4.gif" width="46" height="21 src=">, atunci pentru obținem ecuația unui creion de linii în formă

http://pandia.ru/text/78/223/images/image155_3.gif" width="133" height="23 src=">=0.

Această ecuație determină toate liniile fasciculului, cu excepția liniei date de ecuație , deoarece .

II. Geometrie analitică în spațiu

Geometrie analitică în spațiu

În geometria analitică în spațiu, ca și în geometria analitică în plan, fiecare problemă, oricât de complexă, se reduce la unele probleme cele mai simple. Astfel de probleme, de exemplu, sunt problema determinării distanței dintre două puncte date, problema împărțirii unui segment într-un raport dat, problema calculării unghiului dintre două segmente date etc. Primele două probleme sunt rezolvate în mod similar cu problemele corespunzătoare din avion.

1. Determinarea distanței dintre două puncte date din spațiu. Să fie date două puncte arbitrare și. Apoi, distanța dintre ele este determinată de formulă

2. Împărțirea unui segment într-un raport dat. Să fie date două puncte arbitrare http://pandia.ru/text/78/223/images/image158_3.gif" width="91" height="24 src="> apoi coordonatele punctului de pe linia care împarte segment într-un anumit raport http://pandia.ru/text/78/223/images/image165_3.gif" width="81" height="41">, , ,

unde http://pandia.ru/text/78/223/images/image169_3.gif" width="36" height="19 src=">:

Pentru a rezolva alte probleme simple de geometrie analitică spațială, este convenabil să se utilizeze astfel de operații pe vectori ca adunare vectorială, înmulțire vectorială cu un număr, înmulțire scalară a vectorilor, multiplicare vectorială a vectorilor. Definiția și principalele proprietăți ale acestor operații pe vectori vor fi luate în considerare mai târziu.

3. Ecuația unui plan.

3.1. Ecuația generală a planului. Ecuația liniară a formei

Obțineți textul integral

se numește ecuația generală a planului.

Coeficienții și în această ecuație au semnificația coordonatelor vectorului normal la plan.

Ecuația unui plan care trece printr-un punct are forma

Exemplu. Scrieți o ecuație pentru un plan care trece printr-un punct http://pandia.ru/text/78/223/images/image179_4.gif" width="207" height="21 src="> sau

Dacă două ecuații definesc același plan, atunci coeficienții lor sunt proporționali:

Să luăm în considerare câteva cazuri particulare ale ecuației generale a planului.

1) În ecuația planului http://pandia.ru/text/78/223/images/image188_3.gif" width="113" height="21"> și definește planul care trece prin origine.

2) În ecuația plană http://pandia.ru/text/78/223/images/image190_3.gif" width="108" height="21">.gif" width="60" height="21" > .gif" width="23" height="19 src="> și planul în sine este paralel cu această axă, treceți prin ea.

3) În ecuația plană http://pandia.ru/text/78/223/images/image189_3.gif" width="44" height="19 src="> Ecuația plană ia forma și definește un plan paralel la plan de coordonate, sau potrivirea acestuia. Într-adevăr, în acest caz, un vector normal cu coordonate are proiecții zero pe axele ="23" height="19 src="> iar planul în sine este paralel cu aceste axe, treceți prin ele. Prin urmare, planul este paralel cu planul de coordonate. Același lucru poate fi verificat în alt mod. Să reprezentăm ecuația sub forma și să setăm Ecuația planului va lua forma http://pandia.ru/text/78/223/images/image199_2.gif" width="39" height="15 src=" >.gif" width="13 " height="15">.gif" width="41" height="19">, atunci așa este; în acest caz, planul în cauză coincide cu planul ..gif" width="29" height="21">.