1. Sistem de coordonate dreptunghiular pe plan
Un sistem de coordonate dreptunghiular pe un plan este format din două axe de coordonate reciproc perpendiculare X"Xși Y"Y O, care se numește origine, fiecare axă are o direcție pozitivă. LA mana dreapta sistem de coordonate, direcția pozitivă a axelor este aleasă astfel încât cu direcția axei Y"Y sus, axa X"X privi spre dreapta.
Patru unghiuri (I, II, III, IV) formate din axele de coordonate X"Xși Y"Y, sunt numite unghiuri de coordonate sau cadrane (vezi Fig. 1).
Poziția punctului A pe plan este determinată de două coordonate Xși y. Coordona X egală cu lungimea segmentului OB, coordonate y- lungimea segmentului OCîn unităţile de măsură selectate . Segmente OBși OC definite de linii trasate dintr-un punct A paralel cu axele Y"Yși X"X respectiv. Coordona X numit abscisă puncte A, coordonate y - ordonată puncte A. Scris astfel: A X, y)
Dacă punct A se află în unghiul de coordonate I, apoi punctul A are abscisă și ordonată pozitive. Dacă punct A se află în unghiul de coordonate II, apoi punctul A are o abscisă negativă și o ordonată pozitivă. Dacă punct A se află în unghiul de coordonate III, apoi punctul A are abscisă și ordonată negativă. Dacă punct A se află în unghiul de coordonate IV, apoi punctul A are o abscisă pozitivă și o ordonată negativă.
2. Coordonate polare.
O grilă polară cu mai multe unghiuri marcate în grade.
Sistemul de coordonate polare- un sistem de coordonate bidimensional în care fiecare punct din plan este determinat de două numere - un unghi și o distanță. Sistemul de coordonate polare este util în special atunci când relațiile dintre puncte sunt mai ușor de reprezentat ca distanțe și unghiuri; în sistemul de coordonate carteziene sau carteziene mai obișnuit, astfel de relații pot fi stabilite doar prin aplicarea ecuațiilor trigonometrice.
Sistemul de coordonate polare este dat de o rază, care se numește axa zero sau polară. Punctul din care iese această rază se numește origine sau pol. Orice punct din plan este definit de două coordonate polare: radială și unghiulară. Coordonată radială (de obicei notat r) corespunde distanței de la punct la origine. Coordonata unghiulară, numită și unghi polar sau azimut și notată cu φ, este egală cu unghiul cu care axa polară trebuie rotită în sens invers acelor de ceasornic pentru a ajunge în acel punct.
Coordonata radială determinată în acest fel poate lua valori de la zero la infinit, iar coordonata unghiulară variază de la 0° la 360°. Cu toate acestea, pentru comoditate, intervalul de valori ale coordonatei polare poate fi extins dincolo de unghiul complet și, de asemenea, poate fi permis să ia valori negative, ceea ce corespunde rotației axei polare în sensul acelor de ceasornic.
3. Divizarea segmentelor în acest sens.
Este necesară împărțirea segmentului AB care leagă punctele A(x1;y1) și B(x2;y2) într-un raport dat λ > 0, adică jpg" align="left" width="84 height=84" height =" 84">
Soluţie: Să luăm în considerare vectorii 15 src="> adică și i.e..
Ecuația (9.1) ia forma
Dat fiind vectori egali având coordonate egale, obținem:
http://pandia.ru/text/78/214/images/image014_27.gif" width="56 height=28" height="28"> (9.2) și
http://pandia.ru/text/78/214/images/image016_26.gif" width="60 height=29" height="29"> (9,3)
Se numesc formulele (9.2) și (9.3). formule de diviziune pe segmente în acest sens. În special, pentru λ = 1, adică gif" width="54" height="29 src=">. În acest caz, punctul M(x;y) este mijlocul segmentului AB.
Cometariu:
Dacă λ = 0, atunci aceasta înseamnă că punctele A și M coincid dacă λ< 0, то точка Μ лежит вне отрезка АВ - говорят, что точка M делит отрезок АВ внешним образом , т. к. в противном случае , т. е. AM + MB = 0, т. е. АВ = 0).
4. Distanța dintre puncte.
Este necesar să se găsească distanța d dintre punctele A(x1;y1) și B(x2;y2) ale planului.
Soluţie: Distanța dorită d este egală cu lungimea vectorului, adică. 
5. Ecuația unei drepte care trece prin două puncte.
Dacă două puncte arbitrare M1(x1, y1, z1) și M2(x2, y2, z2) sunt marcate pe o dreaptă în spațiu, atunci coordonatele acestor puncte trebuie să satisfacă ecuația dreptei obținute mai sus:
În plus, pentru punctul M1 putem scrie:
Rezolvând împreună aceste ecuații, obținem:
.
Aceasta este ecuația unei drepte care trece prin două puncte din spațiu.
6. Determinanți de ordinul 2.
Valoarea determinantului de ordinul 2 este ușor de calculat prin definiție folosind o formulă.
7. Determinanți de ordinul 3.
http://pandia.ru/text/78/214/images/image030_15.gif" width="120" height="61 src="> schema de calcul a determinantului folosind metoda triunghiului, adică:
http://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="183" height="73 src=">
Să considerăm un sistem de 3 ecuații liniare cu trei necunoscute:
http://pandia.ru/text/78/214/images/image039_14.gif" width="79" height="46">.gif" width="264" height="48">.gif" width= "120" height="29">.gif" width="110" height="46 src=">
Luați în considerare matricea sistemului și coloanele matricei de termeni necunoscuți și liberi
Să găsim produsul
http://pandia.ru/text/78/214/images/image049_13.gif" width="108" height="41"> sau mai scurt A∙X=B.
Aici matrice Ași B sunt cunoscute, iar matricea X necunoscut. Trebuie găsit, deoarece elementele sale sunt soluția acestui sistem. Această ecuație se numește ecuația matriceală.
Fie determinantul matricei diferit de zero | A| ≠ 0. Atunci ecuația matriceală se rezolvă după cum urmează. Înmulțiți ambele părți ale ecuației din stânga cu matricea A-1, inversul matricei A: http://pandia.ru/text/78/214/images/image051_13.gif" width="168" height="59"> 
Rezolvați următorul sistem de ecuații într-o manieră matriceală:
Atenție: Zerourile apar dacă nu există o variabilă, adică, de exemplu, dacă X3 nu este dat în condiție, atunci este automat egal cu zero. La fel și cu X1 și X2
http://pandia.ru/text/78/214/images/image057_9.gif" width="56 height=54" height="54">
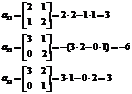
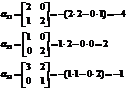
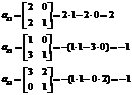
http://pandia.ru/text/78/214/images/image065_8.gif" width="160 height=51" height="51">
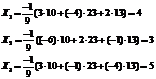Răspuns:
# o anumită:
http://pandia.ru/text/78/214/images/image074_5.gif" width="59 height=16" height="16">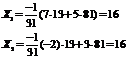 
Răspuns:
http://pandia.ru/text/78/214/images/image081_5.gif" width="106" height="50 src=">
Să găsim matricea inversă.
Scădeți primul rând din toate rândurile de sub el. Această acțiune nu contrazice transformările matriceale elementare.
http://pandia.ru/text/78/214/images/image083_4.gif" width="172" height="52 src=">
Scădeți al 3-lea rând din toate rândurile de deasupra acestuia. Această acțiune nu contrazice transformările matriceale elementare.
http://pandia.ru/text/78/214/images/image085_5.gif" width="187" height="53 src=">
Aducem toți coeficienții de pe diagonala principală a matricei la 1. Împărțim fiecare rând al matricei la coeficientul acestui rând situat pe diagonala principală, dacă nu este egal cu 1. Matricea pătrată, care s-a dovedit la dreapta matricei unităților, este inversul celei principale.
http://pandia.ru/text/78/214/images/image087_4.gif" width="172" height="52 src=">
11. Vectori. Adăugarea vectorilor.
http://www. bigpi. *****/encicl/articles/15/1001553/1001553A. htm
Vector ei numesc o mărime caracterizată printr-o valoare numerică, o direcție în spațiu și dezvoltându-se geometric cu o altă valoare similară.
Grafic, vectorii sunt reprezentați ca segmente de linie direcționată de o anumită lungime, ca http://pandia.ru/text/78/214/images/image089_5.gif" width="17" height="17 src=">.jpg " alt= "(!LANG: adunare vectorială a+b=b+a, a+(b+c)=(a+b)+c" width="110" height="46">!}
Teorema: Oricare ar fi cele trei puncte A, B și C, egalitatea vectorială este valabilă
Când se adaugă Două vectorii folosesc adesea așa-numitul „ regula paralelogramului". În acest caz, un paralelogram este construit folosind termenii vectorilor ca laturi adiacente. Diagonala paralelogramului, trasă din punctul în care sunt conectate începuturile vectorilor, este suma dorită (Fig. 4, stânga).
Este ușor de observat (Fig. 4, dreapta) că această regulă duce la același rezultat ca metoda de mai sus. Când adăugați mai mult de doi vectori " regula paralelogramului» practic nu este folosit din cauza constructiilor greoaie. Adunarea vectorială este comutativă, adică
A + b = b + A.
Și totuși, suma unui anumit număr de vectori nu depinde de ordinea în care sunt adăugați, adică ( A + b) + d = A + (b + d). În acest caz, spunem că adăugarea vectorilor este asociativă, adică legea asociativă este valabilă pentru aceasta.
12. Produsul scalar al vectorilor.
http://www. dpva. info/Ghid/GhidMathematics/linearAlgebra/ScalarVectorsMultiplication/
Produsul scalar al vectorilor este o operație pe doi vectori care are ca rezultat un număr (nu un vector).
http://pandia.ru/text/78/214/images/image097_5.gif" width="86" height="23">
Cu alte cuvinte, produsul scalar al vectorilor este egal cu produsul lungimilor acestor vectori și cosinusul unghiului dintre ei. De remarcat că unghiul dintre doi vectori este unghiul pe care aceștia îl formează dacă sunt amânați dintr-un punct, adică începuturile vectorilor trebuie să coincidă.
Următoarele proprietăți simple rezultă direct din definiție:
1. Produsul scalar al unui vector arbitrar a și însuși (pătratul scalar al vectorului a) este întotdeauna nenegativ și este egal cu pătratul lungimii acestui vector. Mai mult, pătratul scalar al unui vector este egal cu zero dacă și numai dacă vectorul dat este zero.
2. Produsul scalar al oricăror vectori perpendiculari a și b este egal cu zero.
3. Produsul scalar a doi vectori este egal cu zero dacă și numai dacă sunt perpendiculari sau cel puțin unul dintre ei este zero.
4. Produsul scalar al doi vectori a și b este pozitiv dacă și numai dacă există un unghi ascuțit între ei.
5. Produsul scalar a doi vectori a și b este negativ dacă și numai dacă există un unghi obtuz între ei.
O definiție alternativă a produsului scalar sau calculul produsului scalar a doi vectori dat de coordonatele lor.
(Este foarte ușor să calculați coordonatele unui vector având în vedere coordonatele sale de început și de sfârșit.:
Să fie un vector AB, A - începutul vectorului, B - sfârșitul și coordonatele acestor puncte
A=(a1,a2,a3), B=(b1,b2,b3)
Atunci coordonatele vectorului AB:
AB=(b1-a1, b2-a2, b3-a3) .
În mod similar, în spațiul bidimensional - pur și simplu nu există coordonate a treia)
Deci, să fie dați doi vectori dați de o mulțime de coordonate:
a) În spațiul bidimensional (pe un plan)..gif" width="49" height="19 src=">
Apoi produsul lor scalar poate fi calculat prin formula:
b) În spațiul tridimensional: ;
Similar cu cazul bidimensional, produsul lor scalar este calculat prin formula:
http://pandia.ru/text/78/214/images/image103_3.gif" width="78" height="23 src=">.gif" width="98" height="24 src=">
Lungimea vectorului b este calculată în mod similar.
Mijloace, 
, 
Se găsește unghiul dorit.
13. Produs vectorial.
http://www. dpva. info/Ghid/GhidMathematics/linearAlgebra/vectorVectorsMultiplication/
Produsul vectorial al doi vectori a și b este o operație asupra lor, definită doar în spațiul tridimensional, al cărei rezultat este vector cu urmatoarele proprietati:
http://pandia.ru/text/78/214/images/image111_3.gif" width="83" height="27">, unde Ași b.
3) Vectorul este direcționat în așa fel încât dacă aduceți vectorul http://pandia.ru/text/78/214/images/image117_3.gif" width="13" height="24 src=">. gif" width=" 13" height="24"> înainte ca vectorul să fie în sens antiorar.
Pentru o mai mare claritate, să dăm un exemplu - în figura din dreapta, vectorul - produs vectorial vectorii a și b. După cum se precizează în definiție, am adus toți cei trei vectori la un început comun și apoi, dacă vă uitați la vectorii a și b de la sfârșitul vectorului, cea mai scurtă întoarcere de la vectorul a la vectorul b va fi în sens invers acelor de ceasornic.
http://pandia.ru/text/78/214/images/image119_3.gif" width="76" height="25">
De asemenea, direct din definiție rezultă că pentru orice factor scalar k (număr) este adevărat: 
det A http://pandia.ru/text/78/214/images/image182_2.gif" width="56 height=32" height="32">
7.2 Aflarea determinantului unei matrice de ordinul 3 după regula unui triunghi
http://pandia.ru/text/78/214/images/image186_2.gif" width="132" height="45">
Fiecărui element al Matricei pătrate (a cărui ordine este mai mare sau egală cu trei) i se pot atribui două numere, numite MINOR sau COMPLEMENT ALGEBRIC. Minorul elementului Aij al pătratului Matricea A (de orice ordin) este DETERMINANTUL MATRICEI, obținut din Matricea A prin ștergerea rândului și coloanei la intersecția cărora se află elementul Aij. Semnul M - Desemnare minoră.
http://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="35" height="19">
http://pandia.ru/text/78/214/images/image194_1.gif" width="96 height=82" height="82">
ELEMENTE | Minor | Complement algebric |
||||||||||||||||
Fie A \u003d o matrice de ordinul III, atunci determinantul matricei A este egal cu:
Notă: determinantul poate fi calculat peste elemente orice coarde sau orice coloane din această Matrice.
# Găsiți determinantul Matricei după elementele primului rând și ale primei coloane:
http://pandia.ru/text/78/214/images/image201_0.gif" width="58" height="56 src=">
http://pandia.ru/text/78/214/images/image203_0.gif" width="253" height="34 src=">
7.3 determinant al matricei de ordinul n-lea
Fie A o matrice pătrată de ordinul n. Apoi, determinantul matricei de ordinul al n-lea va arăta astfel:
Extinderea elementelor unui rând pentru a găsi elementele matricei A
http://pandia.ru/text/78/214/images/image206_0.gif" width="38" height="55">
6. Dacă într-un rând sau coloană a determinantului, respectiv, se adună elementele altui rând sau coloană, înmulțite cu același număr, atunci determinantul nu își va modifica valoarea.
http://pandia.ru/text/78/214/images/image208_0.gif" width="48" height="12"> etc.
determinant triunghiular- acesta este determinantul pentru care toate elementele situate deasupra (sau dedesubt) diagonalei principale sunt zerouri, egale cu produsul elementelor diagonalei principale.
http://pandia.ru/text/78/214/images/image210_0.gif" width="37" height="28 src=">.gif" width="13 height=25" height="25"> )
Notăm ∆ =det A. Pentru ca Matricea pătrată A să aibă inversă, este necesar și suficient ca Matricea să fie nedegenerată (alta decât zero). Inversul matricei A se notează cu A-1, deci B = A-1. Matricea inversă se calculează cu formula: C p - distanța de la origine la plan.
http://pandia.ru/text/78/214/images/image248.gif" width="110" height="36 src=">
Aici http://pandia.ru/text/78/214/images/image250.gif" width="29" height="13"> este arbitrar dacă D=0.
21. Curbele a 2-a (ecuația cercului).
Definiție 11.1.Curbe de ordinul doi pe un plan se numesc liniile de intersecție a unui con circular cu plane care nu trec prin vârful acestuia.
Dacă un astfel de plan intersectează toți generatorii unei cavități a conului, atunci în secțiune se dovedește elipsă, la intersecția generatoarelor ambelor cavități - hiperbolă, iar dacă planul de tăiere este paralel cu orice generatoare, atunci secțiunea conului este parabolă.
Cometariu. Toate curbele de ordinul doi sunt date de ecuații de gradul doi în două variabile.
Clasificarea curbelor de ordinul doi
Curbe nedegenerate
nedegenerat dacă pot apărea următoarele opțiuni:
Curbă nedegenerată de ordinul doi se numește central dacă
elipsă – prevăzută D> 0 și ∆ eu < 0;
un caz special al unei elipse - un cerc - furnizat eu 2 = 4D sau A 11 = A 22,A 12 = 0;
elipsă imaginară (fără punct real) - supusă Δ eu > 0;
hiperbolă – supusă D < 0;
O curbă nedegenerată de ordinul doi se numește necentrală dacă Δ eu = 0
parabolă – supusă D = 0.
Curbe degenerate: Se numește curba de ordinul doi degenerat dacă Δ = 0. Pot apărea următoarele opțiuni:
punct real la intersecția a două drepte imaginare (elipsă degenerată) – prevăzut D > 0;
o pereche de linii reale care se intersectează (hiperbolă degenerată) - în condiția D < 0;
parabolă degenerată – prevăzută D = 0:
o pereche de linii paralele reale - prevăzute B < 0;
o linie reală (două linii paralele îmbinate) - prevăzută B = 0;
o pereche de drepte paralele imaginare (nu un singur punct real) - prevăzute B > 0.
22. Elipsa și ecuația ei.
Definiție 11.2.Elipsă este mulţimea punctelor din plan pentru care suma distanţelor la două puncte fixe F 1 și F 2 din acest avion, numit trucuri, este o valoare constantă.
Cometariu. Când punctele se potrivesc F 1 și F 2 elipsa se transformă într-un cerc.
Deducem ecuația elipsei alegând sistemul cartezian: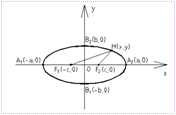 
coordonate astfel încât axa Oh a coincis cu linia F 1F 2, originea coordonatelor - cu mijlocul segmentului F 1F 2.
Fie lungimea acestui segment 2 Cu, apoi în sistemul de coordonate ales F 1(-c, 0), F 2(c, 0). Lasă punctul M(x, y) se află pe elipsă, iar suma distanțelor de la aceasta până la F 1 și F 2 este egal cu 2 A.
Apoi r 1 + r 2 =2A, dar http://pandia.ru/text/78/214/images/image255.gif" width="103" height="25 src="> ,
Prin urmare http://pandia.ru/text/78/214/images/image257.gif" width="60" height="35 src="> (11.1)
Definiție 11.3.excentricitate elipsa se numește cantitate e=c/a (11.2)
Definiție 11.4.Directoarea Di elipsă corespunzătoare focalizării fi, se numește dreptă situată în același semiplan cu fi despre axa OU perpendicular pe ax Oh pe distanta a/e de la origine.
Cometariu. Cu o alegere diferită a sistemului de coordonate, elipsa poate fi dată nu de ecuația canonică (11.1), ci de o ecuație de gradul doi de alt fel.
Proprietățile elipsei:
1) Elipsa are două axe de simetrie reciproc perpendiculare (axele principale ale elipsei) și un centru de simetrie (centrul elipsei). Dacă o elipsă este dată de o ecuație canonică, atunci axele sale principale sunt axele de coordonate, iar centrul este originea. Deoarece lungimile segmentelor formate prin intersecția elipsei cu axele principale sunt egale cu 2 Ași 2 b (2A>2b), atunci axa principală care trece prin focare se numește axa majoră a elipsei, iar a doua axă majoră se numește axa mică.
2) Întreaga elipsă este cuprinsă într-un dreptunghi http://pandia.ru/text/78/214/images/image029_18.gif" width="12" height="19 src=">
3) Excentricitatea elipsei e< 1.
Hiperbolă.Definiția 11.5.Hiperbolă este mulţimea punctelor din plan pentru care modulul diferenţei dintre distanţele la două puncte fixe F 1 și F 2 din acest avion, numit trucuri, este o valoare constantă.http://pandia.ru/text/78/214/images/image265.gif" width="180" height="29">. b² = c² - A², de aici puteți obține http://pandia.ru/text/78/214/images/image267.gif" width="38" height="30 src=">.gif" width="87" height= „44 src="> , (11,3`)
pentru care axele reale și imaginare sunt interschimbate păstrând aceleași asimptote.
4) Excentricitatea hiperbolei e> 1.
5) Raportul distanței ri de la punctul de hiperbola la focalizare fi la distanta di din acest punct până la directriza corespunzătoare focarului este egală cu excentricitatea hiperbolei.
Dovada poate fi efectuată în același mod ca și pentru elipsă.
23. Parabolă.
Definiția 11.8.parabolă este mulțimea de puncte din plan pentru care distanța până la un punct fix F acest plan este egal cu distanța până la o linie dreaptă fixă. Punct F numit se concentreze parabole și o linie dreaptă - este directoare.
Pentru a deriva ecuația parabolei, alegem un sistem de coordonate carteziene astfel încât originea lui să fie punctul mijlociu al perpendicularei FD, coborât de la focalizare la directrice, iar axele de coordonate erau paralele și perpendiculare pe directrice. Fie lungimea segmentului FD
D O F x este R. Apoi de la egalitate r = d rezultă că http://pandia.ru/text/78/214/images/image271.gif" width="101 height=38" height="38">,
Prin transformări algebrice, această ecuație poate fi redusă la forma:
y² = 2 px, (11.4) numit ecuația canonică a parabolei.
Valoare R numit parametru parabole.
Proprietățile parabolelor :
1) Parabola are o axă de simetrie (axa parabolei). Punctul de intersecție al parabolei cu axa se numește vârful parabolei. Dacă parabola este dată de ecuația canonică, atunci axa ei este axa Oh, iar vârful este originea coordonatelor.
2) Întreaga parabola este situată în semiplanul drept al planului Ohu.
Cometariu. Folosind proprietățile directricelor unei elipse și unei hiperbole și definiția unei parabole, putem demonstra următoarea afirmație:
Mulțimea punctelor plane pentru care raportul e distanța până la un punct fix până la distanța până la o linie dreaptă este o valoare constantă, este o elipsă (cu e<1), гиперболу (при e>1) sau o parabolă (când e=1).
Reducerea ecuației de ordinul doi la forma canonică.
Definiție 11.9. Linie definită de o ecuație generală de ordinul doi
http://pandia.ru/text/78/214/images/image274.gif" width="103 height=19" height="19"> puteți seta matricea
http://pandia.ru/text/78/214/images/image276.gif" width="204" height="24 src="> (presupunând că λ 1,2 nu sunt egale cu 0).
Să stabilim transferul paralel ulterior prin formulele: , .
Obținem ecuația în noul sistem de coordonate. (11,7)
Luați în considerare posibilele imagini geometrice definite de această ecuație în funcție de semne λ
Sistem de coordonate dreptunghiular în spațiu format din trei axe de coordonate reciproc perpendiculare BOU, OYși oz. Axele de coordonate se intersectează într-un punct O, care se numește origine, pe fiecare axă este selectată direcția pozitivă indicată de săgeți, iar unitatea de măsură a segmentelor de pe axe. Unitățile de măsură sunt de obicei aceleași pentru toate axele (ceea ce este opțional). BOU- axa absciselor, OY- axa y, oz- axa aplicatiei.
Dacă degetul mare al mâinii drepte este luat ca direcție X, indicând direcția Y, și media pe direcție Z, apoi se formează dreapta sistem de coordonate. Degetele similare ale mâinii stângi formează sistemul de coordonate stânga. Cu alte cuvinte, direcția pozitivă a axelor este aleasă astfel încât atunci când axa este rotită BOUîn sens invers acelor de ceasornic cu 90° direcția sa pozitivă a coincis cu direcția pozitivă a axei OY, dacă această rotație este observată din partea direcției pozitive a axei oz. Sistemele de coordonate dreapta și stânga nu pot fi combinate astfel încât axele corespunzătoare să coincidă (vezi Fig. 2).
Poziția punctului Aîn spațiu este determinată de trei coordonate X, yși z. Coordona X egală cu lungimea segmentului OB, coordonate y- lungimea segmentului OC, coordonate z- lungimea segmentului ODîn unitățile de măsură selectate. Segmente OB, OCși OD sunt definite de planuri trasate dintr-un punct A paralel cu planele YOZ, XOZși XOY respectiv. Coordona X numită abscisa punctului A, coordonate y- punct de ordonat A, coordonate z- punctul de aplicare A. Ei o notează astfel:
Înainte de a discuta despre mecanismele transformării imaginii, să definim condițiile de fixare a poziției, care fac posibilă arătarea relației dintre obiecte (elemente) înainte și după transformări.
Sistemul de reguli, relații și mijloace vizuale (grafice) care vă permite să stabiliți (determinați) poziția obiectului de atenție pe un plan sau în spațiu este definit ca un sistem de referință, un sistem de coordonate (CS), conform căruia unui set de numere (coordonate) este atribuit fiecărui punct din spațiu). Numărul de coordonate care sunt necesare pentru a descrie poziția unui punct determină dimensiunea spațiului și, în consecință, prezența graficelor bidimensionale și tridimensionale. Grafica bidimensională utilizează două concepte - înălțime și lățime și nu provoacă dificultăți deosebite atunci când lucrați cu o imagine. Conceptul de grafică tridimensională conține o indicație că va trebui să lucrați cu trei dimensiuni spațiale - înălțime, lățime și adâncime. Fără a intra în subtilitățile conceptului de „grafică tridimensională”, observăm că atunci când lucrați cu mijloace grafice de grafică pe computer, este necesar să ne amintim că imaginile create ale obiectelor reale există doar în memoria computerului. Nu au o formă fizică, deoarece nu sunt altceva decât un set de ecuații matematice și mișcarea electronilor în microcircuite. Și din moment ce aceste obiecte nu pot exista în afara unui computer, singura modalitate de a le vedea în lumină reală este adăugarea de noi ecuații care descriu condițiile de iluminare și punctele de vedere.
Principala diferență dintre grafica bidimensională și grafica tridimensională este absența completă a unei a treia coordonate în obiectele bidimensionale (imagini) - adâncimea, valoare care caracterizează proprietățile spațiale ale unui obiect. Figurile din avion sunt caracterizate doar prin lățime și înălțime. Și dacă imaginea dvs. este de așa natură încât creează iluzia prezenței unei a treia componente, atunci orice încercare de a privi obiectul dintr-un unghi diferit va fi întotdeauna asociată cu necesitatea de a redesena obiectul din nou.
Dacă în timpul modelării obiecte tridimensionale dobândesc o coordonată de adâncime, atunci odată ce ați desenat astfel de obiecte, atunci este posibil să le vizualizați din orice unghi de vedere fără redesenare.
Poziția fiecărui punct în spațiu este determinată de un triplu de numere - coordonate (lățime, înălțime și adâncime). Astfel, prin fiecare punct se pot trasa trei axe de coordonate ale spațiului virtual. O axă de coordonate este o linie imaginară în spațiu care definește direcția în care se schimbă o coordonată. Punctul de intersecție a celor trei axe, care are coordonatele (0,0,0) este punctul de origine.
În grafica computerizată, în funcție de natura sarcinilor de rezolvat, de structura reprezentării imaginilor și de procesul de prelucrare a datelor grafice, se folosesc diferite coordonate:
polar, cilindric, sferic;
relativ;
utilizator;
fizic;
normalizat;
omogen.
coordonata mondiala se referă la o coordonată carteziană independentă de dispozitiv utilizată într-un program de aplicație atunci când se specifică date grafice de intrare și ieșire. Vom spune că un sistem de coordonate dreptunghiular carteziene este stabilit pe plan dacă se definește o pereche de axe reciproc perpendiculare și în același timp se determină care dintre aceste axe este axa ordonatelor, care este axa absciselor, precum și o un singur segment (la scară) de-a lungul axelor. Pe fig. 3.14 prezintă un sistem de coordonate carteziene și un punct definit pe acesta M. Aruncă din punct M perpendiculare pe ax BOUși OY. Punctele de intersecție ale acestor perpendiculare cu axele de coordonate sunt marcate corespunzător Lși K. Abscisa punctului M este segmentul axei OX, iar ordonata este valoarea segmentului axei Y. Câteva numere Xși y, Unde x= , y= numit coordonatele punctului Mîn sistemul de coordonate selectat. Faptul că punctul M are coordonate Xși y este scris asa: M(x,y).În acest caz, se scrie mai întâi abscisa și apoi ordonata punctului M.
Astfel, fiecare punct M planul corespunde unei perechi de numere reale ( X y) sunt coordonatele acestui punct. Invers, fiecare pereche de numere reale ( X y) corespunde și numai unui punct M planul pentru care aceste numere vor fi coordonatele sale.
În consecință, introducerea în plan a cartezianului sistem dreptunghiular coordonate vă permite să stabiliți o corespondență unu-la-unu între setul de puncte din plan și setul de perechi de numere reale din plan. Această corespondență face posibilă reducerea studiului mulțimilor de puncte pe un plan la studiul mulțimilor de perechi de numere reale, adică aplicarea metodelor algebrice la studiul problemelor de geometrie. Aceeași corespondență face posibilă interpretarea geometrică unor întrebări de algebră și alte discipline.
Având în vedere aspectul aplicat al CS, trebuie reținut următoarele. Deoarece coordonatele sunt în mod inerent fără dimensiuni, poziționarea obiectelor se face în unități care sunt naturale aplicației și utilizatorului. De exemplu, doriți să afișați un grafic al producției lunare pentru un an. Coordonatele din acest CS ( X- luna; y- ieșire) sunt numite coordonatele utilizatorului, și deoarece vă permit să specificați obiecte în lumea bidimensională și tridimensională, ele mai sunt numite coordonate globale.
Dacă în spațiul vectorial considerat nu se presupune că este posibil să se compare lungimile vectorilor unitari (ort), |e 1 |, |e 2 |, |e 3 |, atunci acest spațiu se numește afin. Un spațiu vectorial afin permite studierea proprietăților generale ale figurilor care se modifică cu o transformare arbitrară a sistemului de coordonate. Sistemele de coordonate afine și carteziene de pe plan stabilesc o corespondență unu-la-unu între puncte și coordonate.
Un sistem de coordonate afine sau carteziene se numește drept dacă alinierea semiaxei pozitive X cu axa pozitiva la realizat prin rotirea axei Bouîn direcția opusă direcției mișcării în sensul acelor de ceasornic cu un unghi mai mic de p. În caz contrar, sistemul de coordonate se numește stânga.
Dacă segmentele sunt egale (cazul unui spațiu vectorial metric), iar unghiul dintre axe ¹90 0 KS se numește oblic. Adică, pe lângă CS carteziană, există și alte sisteme de coordonate care vă permit să determinați poziția unui punct pe un plan (spațiu) folosind perechi (triple) de numere reale. Astfel de CS includ, de exemplu, polar sistem de coordonate.
Sistemul de coordonate polare. Definiți un punct pe plan O iar axa care trece prin ea OP. Punct O Hai sa sunăm stâlp, o semiaxă (fascicul) , iesind dintr-un punct Oîntr-o direcție pozitivă - axa polară. Specificarea polului axei polare OPși un singur segment (la scară). OE defineste in plan sistem de coordonate polare. Raza polară r orice punct M se numeste lungimea segmentului. unghi polar j puncte M numit unghi de înclinare a segmentului direcționat față de axa polară OP. Colţ j se determină ținând cont de semn și până la un termen al formularului 2kp, Unde k-întreg.
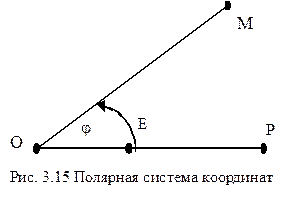Numerele rși j, raza polară și unghiul polar al unui punct M, numit coordonate polare. Un punct cu coordonate polare se notează după cum urmează: M(r,j) sau ( r,j) .
Astfel, atribuirea oricărei perechi de numere reale ( r,j), ³ 0 vă permite să construiți un punct pe plan M, pentru care aceste numere sunt coordonatele sale polare.
Când creați imagini, destul de des este necesar să folosiți atât coordonatele carteziene dreptunghiulare, cât și coordonatele polare ale punctelor. De interes practic sunt formulele care fac posibilă calcularea din coordonate carteziene coordonate polare si invers.
Lasă punctul M punct arbitrar al planului , Xși y sunt coordonatele sale carteziene, r, j - polar. pentru că
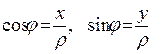
Formulele (1) exprimă coordonatele carteziene dreptunghiulare ale punctului M prin coordonate polare.
adică deci
Formulele (2) ne permit să determinăm coordonatele polare ale punctului M prin coordonatele sale carteziene. Dacă punct M nu se află pe axa OY, atunci formulele (2) implică relația
coordonata fizica luați în considerare coordonatele specificate în sistemul de coordonate, care depinde de dispozitiv.
Coordonate normalizate apelați o coordonată specificată într-un sistem de coordonate intermediar, independent de dispozitiv și normalizată în raport cu un anumit interval, de obicei de la 0 la 1. În acest caz, imaginea exprimată în coordonate normalizate este situată în aceeași poziție relativă atunci când este redată la orice dispozitiv. Coordonatele normalizate sunt utilizate dacă aria spațiului tridimensional este delimitată de un cub cu o latură h mapat la aceeași zonă delimitată de un cub cu latură b",în acest caz, se utilizează un factor de normalizare, împărțirea la care se obțin coordonatele normalizate. Coordonatele sistemului mondial sunt uneori reduse la o formă normalizată.
sala de instrumente sistemul de coordonate este întotdeauna normalizat. Coordonatele sunt de obicei date în zecimale de la 0 la 1 sau în unități întregi, cum ar fi un raster de ecran de afișare (dimensiune 1024 X 10*4 unități raster).
Sistemul de coordonate omogen este utilizat pe scară largă în grafica computerizată și permite reprezentarea unui obiect n-dimensional în (n +1) - spațiu dimensional, prin adăugarea unei coordonate suplimentare - un factor scalar. Coordonatele omogene sunt principalele în geometria proiectivă, în grafica computerizată sunt o tehnică artificială convenabilă care vă permite să linearizați imaginile în perspectivă. Coordonatele omogene fac posibilă înregistrarea punctelor necorespunzătoare (infinit îndepărtate) ale spațiului, precum și exprimarea transformărilor afine într-o formă convenabilă de matrice, evitând depășirea rețelei de biți a computerului din cauza normalizării numerelor.
Coordonatele omogene sunt definite după cum urmează. Să fie dat un sistem de coordonate afine și un punct arbitrar pe plan R cu coordonate (X y). Să introducem un sistem de coordonate în care o a treia componentă este introdusă pentru a descrie vectorul de poziție al unui punct. Hai sa sunăm sistem de coordonate omogen orice triplu de numere simultan diferite de zero a 1, a 2, a 3, legate prin raport
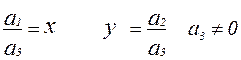
La rezolvarea problemelor de grafică pe computer, coordonatele omogene sunt introduse de obicei după cum urmează: un punct arbitrar M(x, y) pe plan i se atribuie un punct M'(x, y) in spatiu. Rețineți că un punct arbitrar pe linia care leagă originea 0(0, 0, 0) cu punctul M(x, y, 1) poate fi dat printr-un triplu de numere hx, hy, h (hx, hy, h) la h¹0. Un vector definit de un triplu de numere hx, hy, h, este vectorul de direcție al dreptei care leagă punctele 0 și M'. Această linie intersectează planul Z=h la un moment dat ( x, y, h), care definește în mod unic un punct X y plan de coordonate XOY. Adică între punct X yși un set de puncte ( hx, hy, h) h¹0 instalat
Coordonatele din plan și din spațiu pot fi introduse într-un număr infinit de moduri diferite. Și, rezolvând cutare sau cutare problemă geometrică și fizică prin metoda coordonatelor, puteți folosi diferite sisteme de coordonate, alegându-l pe cel în care
sarcina este mai ușor de rezolvat. Luați în considerare unele sisteme de coordonate, altele decât dreptunghiulare.
20.1. Coordonate oblice (afine).
Pe plan ele sunt definite după cum urmează.
Desenăm două drepte arbitrare pe planul printr-un punct dat O și introducem pe fiecare dintre ele o coordonată numărată din punctul O (segmentele de scară de pe axe pot fi de lungimi diferite, Fig. 20.1). Să notăm aceste coordonate XJ și să numim liniile axe, adică în același mod ca în cazul coordonatelor dreptunghiulare, dar acum axele nu se presupune că sunt reciproc perpendiculare.
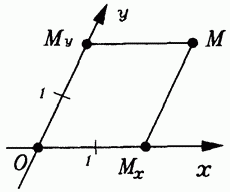
Orice punct M al planului este asociat pe axă cu punctul în care această axă este intersectată de o dreaptă paralelă cu axa y. Definim un punct pe axa y în același mod. Coordonatele oblice ale punctului M sunt coordonatele punctelor de pe axele x și y.
În spațiu, coordonatele oblice sunt introduse după cum urmează. Să trasăm trei drepte arbitrare prin acest punct O care nu se află în același plan și să introducem pe fiecare dintre ele o coordonată numărată din punctul O. Să notăm aceste coordonate cu x, y, z și vom numi aliniază axele
Orice punct M al spațiului corespunde pe axă cu punctul în care această axă intersectează planul care trece prin punctul M, paralel cu planul, iar dacă M se află în plan, atunci presupunem. În mod similar, definim puncte pe axele y și z. Pentru coordonatele x, y, z ale punctului M se iau coordonatele punctelor de pe axele corespunzătoare (Fig. 20.2). Dacă axele sunt reciproc perpendiculare, atunci coordonatele oblice devin dreptunghiulare.
