Preden razpravljamo o mehanizmih transformacije slike, določimo pogoje za fiksiranje položaja, ki omogočajo prikaz razmerja med objekti (elementi) pred in po transformacijah.
Sistem pravil, odnosov in vizualnih (grafičnih) sredstev, ki vam omogočajo nastavitev (določanje) položaja predmeta pozornosti na ravnini ali v prostoru, je opredeljen kot referenčni sistem, koordinatni sistem (CS), po katerem vsaki točki v prostoru je pripisan niz števil (koordinat).). Število koordinat, ki so potrebne za opis položaja točke, določa dimenzijo prostora in s tem prisotnost dvodimenzionalne in tridimenzionalne grafike. Dvodimenzionalna grafika uporablja dva koncepta - višino in širino in ne povzroča posebnih težav pri delu s sliko. Koncept tridimenzionalne grafike vsebuje navedbo, da boste morali delati s tremi prostorskimi dimenzijami - višino, širino in globino. Ne da bi se spuščali v zapletenost koncepta "tridimenzionalne grafike", ugotavljamo, da je treba pri delu z grafičnimi sredstvi računalniške grafike zapomniti, da ustvarjene slike resničnih predmetov obstajajo samo v pomnilniku računalnika. Nimajo fizične oblike, saj niso nič drugega kot niz matematičnih enačb in gibanja elektronov v mikrovezjih. In ker ti predmeti ne morejo obstajati zunaj računalnika, je edini način, da jih vidimo v resnični svetlobi, dodajanje novih enačb, ki opisujejo svetlobne pogoje in zorne kote.
Glavna razlika med dvodimenzionalno grafiko in tridimenzionalno grafiko je popolna odsotnost tretje koordinate v dvodimenzionalnih predmetih (slikah) - globina, vrednost, ki označuje prostorske lastnosti predmeta. Za figure na ravnini sta značilni le širina in višina. In če je vaša slika takšna, da ustvarja iluzijo, da ima tretjo komponento, bo vsak poskus pogleda na predmet iz drugega zornega kota vedno povezan s potrebo po ponovnem risanju predmeta.
Če med modeliranjem tridimenzionalni predmeti pridobijo globinsko koordinato, potem ko narišete takšne predmete, jih je mogoče videti iz katerega koli zornega kota brez ponovnega risanja.
Položaj vsake točke v prostoru določa trojka števil – koordinat (širina, višina in globina). Tako je skozi vsako točko mogoče narisati tri koordinatne osi virtualnega prostora. Koordinatna os je namišljena črta v prostoru, ki določa smer, v kateri se spreminja koordinata. Točka presečišča treh osi, ki ima koordinate (0,0,0), je izhodiščna točka.
V računalniški grafiki se glede na naravo nalog, ki jih rešujemo, od strukture predstavitve slik in od procesa obdelave grafičnih podatkov uporabljajo različne koordinate:
polarni, cilindrični, sferični;
sorodnik;
uporabnik;
fizično;
normalizirano;
homogena.
svetovna koordinata se nanaša na od naprave neodvisno kartezično koordinato, ki se uporablja v aplikacijskem programu pri podajanju grafičnih vhodnih in izhodnih podatkov. Rekli bomo, da je na ravnini postavljen kartezični pravokotni koordinatni sistem, če definiramo par medsebojno pravokotnih osi in hkrati določimo, katera od teh osi je ordinatna os, katera abscisna os in enojni (lestvica) segment vzdolž osi. Na sl. 3.14 prikazuje kartezični koordinatni sistem in na njem določeno točko M. Spustite s točke M pravokotnice na os OX in ojoj. Presečišča teh navpičnic s koordinatnimi osemi so ustrezno označena L in K. Abscisa točke M je odsek osi OX, ordinata pa vrednost odseka osi Y. Nekaj številk x in y, kje x= , y= klical koordinate točke M v izbranem koordinatnem sistemu. Dejstvo, da ima točka M koordinate x in l je napisano takole: M(x,y). V tem primeru najprej zapišemo absciso, nato pa ordinato točke M.
Torej vsaka točka M ravnina ustreza paru realnih števil ( x,y) so koordinate te točke. Nasprotno pa vsak par realnih števil ( x,y) ustreza in samo eni točki M ravnino, za katero bodo te številke njene koordinate.
Posledično uvedba kartezičnega pravokotnega koordinatnega sistema na ravnini omogoča vzpostavitev ujemanja ena proti ena med množico točk na ravnini in množico parov realnih števil na ravnini. Ta korespondenca omogoča zmanjšanje preučevanja množic točk na ravnini na preučevanje množic parov realnih števil, to je uporabo algebraičnih metod pri preučevanju geometrije. Ista korespondenca omogoča geometrično razlago nekaterih vprašanj algebre in drugih disciplin.
Glede na uporabni vidik CS je treba opozoriti na naslednje. Ker so koordinate same po sebi brezrazsežne, se pozicioniranje objektov izvaja v enotah, ki so naravne za aplikacijo in uporabnika. Na primer, želite prikazati graf mesečne proizvodnje za eno leto. Koordinate v tem CS ( x- mesec; l- izhod). uporabniške koordinate, in ker vam omogočajo določanje predmetov v dvodimenzionalnem in tridimenzionalnem svetu, se imenujejo tudi globalne koordinate.
Če v obravnavanem vektorskem prostoru naj ne bi bilo mogoče primerjati dolžin enotskih vektorjev (ort), |e 1 |, |e 2 |, |e 3 |, potem se ta prostor imenuje afin. Afini vektorski prostor omogoča preučevanje splošnih lastnosti likov, ki se spreminjajo s poljubno transformacijo koordinatnega sistema. Afini in kartezični koordinatni sistemi na ravnini vzpostavljajo ujemanje ena proti ena med točkami in koordinatami.
Afini ali kartezični koordinatni sistem se imenuje desni, če je poravnava pozitivne pol osi X s pozitivno osjo pri izvedemo z vrtenjem osi Ox v smeri, ki je nasprotna smeri gibanja urinega kazalca za kot, manjši od p. V nasprotnem primeru se koordinatni sistem imenuje levi.
Če so segmenti enaki (primer metričnega vektorskega prostora) in se imenuje kot med osmi ¹90 0 KS poševno. To pomeni, da poleg kartezičnega CS obstajajo tudi drugi koordinatni sistemi, ki vam omogočajo, da določite položaj točke na ravnini (prostoru) z uporabo parov (trojk) realnih števil. Takšni CS vključujejo npr. polarni koordinatni sistem.
Polarni koordinatni sistem. Določite točko na ravnini O in os, ki poteka skozi to OP. Pika O pokličimo palica, polos (žarek) , ki izhaja iz točke O v pozitivno smer - polarna os. Določitev pola polarne osi OP in en sam (lestvica) segment OE določa na ravnini polarni koordinatni sistem. Polarni radij r katera koli točka M se imenuje dolžina segmenta. polarni kot j točk M imenujemo kot naklona usmerjenega segmenta na polarno os OP. Kotiček j se določi ob upoštevanju znaka in do izraza obrazca 2kp, kje k- celo število.
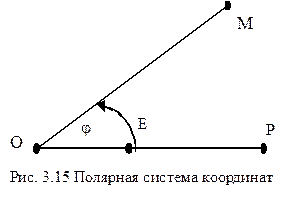Številke r in j, polarni radij in polarni kot točke M, klical polarne koordinate. Točka s polarnimi koordinatami je označena na naslednji način: M(r,j) ali ( r,j) .
Tako je dodelitev katerega koli para realnih števil ( r,j), ³ 0 vam omogoča, da zgradite eno točko na ravnini M, za katero so te številke njegove polarne koordinate.
Pri ustvarjanju slik je pogosto treba uporabiti kartezične pravokotne in polarne koordinate točk. Praktično zanimive so formule, ki omogočajo izračun polarnih koordinat iz kartezičnih koordinat in obratno.
Naj bistvo M poljubna točka ravnine , x in l so njegove kartezične koordinate, r,j- polarni. Ker
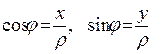
Formule (1) izražajo pravokotne kartezične koordinate točke M skozi polarne koordinate.
torej torej
Formule (2) nam omogočajo določitev polarnih koordinat točke M s svojimi kartezičnimi koordinatami. Če točka M ne leži na osi OY, potem formule (2) implicirajo razmerje
fizična koordinata upoštevajte koordinato, določeno v koordinatnem sistemu, ki je odvisen od naprave.
Normalizirana koordinata pokličite koordinato, določeno v vmesnem, od naprave neodvisnem koordinatnem sistemu in normalizirano glede na določeno območje, običajno od 0 do 1. V tem primeru se slika, izražena z normaliziranimi koordinatami, nahaja v istem relativnem položaju, ko je upodobljena na kateri koli napravo. Normalizirane koordinate se uporabljajo, če je območje tridimenzionalnega prostora omejeno s kocko s stranico h preslikano na isto območje, ki ga omejuje kocka s stranico b", v tem primeru se uporabi normalizacijski faktor, z deljenjem katerega dobimo normalizirane koordinate. Koordinate svetovnega sistema se včasih zmanjšajo na normalizirano obliko.
prostor za instrumente koordinatni sistem je vedno normaliziran. Koordinate so običajno podane v decimalkah v razponu od 0 do 1 ali v celih enotah, kot je raster zaslona (velikost 1024 X 10*4 rastrskih enot).
Homogen koordinatni sistem se pogosto uporablja v računalniški grafiki in omogoča, da se n-dimenzionalni objekt predstavi v (n +1) - dimenzionalnem prostoru z dodajanjem še ene koordinate - skalarnega faktorja. Homogene koordinate so glavne v projektivni geometriji, v računalniški grafiki so priročna umetna naprava, ki vam omogoča linearizacijo perspektivnih slik. Homogene koordinate omogočajo snemanje nepravilnih (neskončno oddaljenih) točk prostora, pa tudi izražanje afinih transformacij v priročni matrični obliki, pri čemer se izognemo prelivanju računalniške bitne mreže zaradi normalizacije števil.
Homogene koordinate so definirane na naslednji način. Naj bo na ravnini podan sistem afinih koordinat in poljubna točka R s koordinatami (x, y). Predstavimo koordinatni sistem, v katerem je uvedena tretja komponenta za opis vektorja položaja točke. Pokličimo homogeni koordinatni sistem katera koli trojka sočasno neničelnih števil a 1, a 2, a 3, povezana z razmerjem
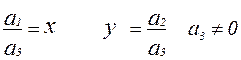
Pri reševanju računalniško grafičnih problemov se homogene koordinate običajno uvedejo na naslednji način: poljubna točka M(x, y) na ravnini je pripisana točka M'(x, y) v vesolju. Upoštevajte, da lahko poljubno točko na premici, ki povezuje izhodišče 0(0, 0, 0) s točko M(x, y, 1), poda trojka števil hx, hy, h (hx, hy, h) pri h¹0. Vektor, definiran s trojko števil hx, hy, h, je smerni vektor premice, ki povezuje točki 0 in M'. Ta premica seka ravnino Z=h na točki ( x, y, h), ki enolično definira točko x, y koordinatna ravnina XOY. Se pravi med točko x, y in niz točk ( hx, hy, h) h¹0 nameščen
Koordinate na ravnini in v prostoru lahko vnašamo na neskončno veliko različnih načinov. In pri reševanju tega ali onega geometrijskega in fizikalnega problema z metodo koordinat lahko uporabite različne koordinatne sisteme, pri čemer izberete tistega, v katerem je dano
nalogo je lažje rešiti. Razmislite o nekaterih koordinatnih sistemih, ki niso pravokotni.
20.1. Poševne (afine) koordinate.
Na ravnini so opredeljeni na naslednji način.
Skozi dano točko O na ravnini narišemo dve poljubni ravni črti in na vsaki od njih vnesemo koordinato, šteto od točke O (odseki na oseh so lahko različnih dolžin, sl. 20.1). Označimo te koordinate XJ in imenujemo črte osi , t.j. na enak način kot v primeru pravokotnih koordinat, vendar zdaj osi ne predpostavljamo, da so medsebojno pravokotne.
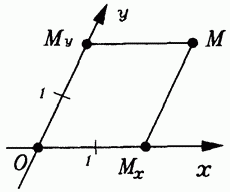
Vsaki točki M na ravnini je na osi pridružena točka, v kateri to os seka premica, vzporedna z osjo y. Podobno določimo točko na osi y. Poševne koordinate točke M so koordinate točk na oseh x in y.
V prostoru se poševne koordinate uvedejo na naslednji način. Skozi dano točko O narišimo tri poljubne premice, ki ne ležijo v isti ravnini, in na vsako od njih vpišimo koordinato, šteto od točke O. Te koordinate označimo z x, y, z in jih imenujemo črte osi
Vsaka točka M prostora ustreza na osi točki, v kateri ta os seka ravnino, ki poteka skozi točko M, vzporedno z ravnino, in če M leži v ravnini, potem predpostavimo. Podobno definiramo točke na ravnini. y in z osi. Za koordinate x, y, z točke M se vzamejo koordinate točk na ustreznih oseh (slika 20.2). Če sta osi medsebojno pravokotni, postanejo poševne koordinate pravokotne.
1. Pravokotni koordinatni sistem na ravnini
Pravokotni koordinatni sistem na ravnini tvorita dve med seboj pravokotni koordinatni osi X"X in Y"Y O, ki se imenuje izhodišče, ima vsaka os pozitivno smer. AT desna roka koordinatnem sistemu je pozitivna smer osi izbrana tako, da s smerjo os Y"Y gor, os X"X pogledal na desno.
Štirje koti (I, II, III, IV), ki jih tvorijo koordinatne osi X"X in Y"Y, se imenujejo koordinatni koti ali kvadranti (glej sliko 1).
Položaj točke A na ravnini je določen z dvema koordinatama x in l. Koordinate x enaka dolžini segmenta OB, koordiniraj l- dolžina segmenta OC v izbranih merskih enotah. Segmenti OB in OC definirana s črtami, ki potekajo iz točke A vzporedno z osemi Y"Y in X"X oz. Koordinate x klical abscisa točke A, koordiniraj l - ordinata točke A. Napisano takole: A x, l)
Če točka A leži v koordinatnem kotu I, nato točka A ima pozitivno absciso in ordinato. Če točka A leži v koordinatnem kotu II, nato točka A ima negativno absciso in pozitivno ordinato. Če točka A leži v koordinatnem kotu III, nato točka A ima negativno absciso in ordinato. Če točka A leži v koordinatnem kotu IV, nato točka A ima pozitivno absciso in negativno ordinato.
2. Polarne koordinate.
Polarna mreža z več koti, označenimi v stopinjah.
Polarni koordinatni sistem- dvodimenzionalni koordinatni sistem, v katerem je vsaka točka na ravnini določena z dvema številoma - kotom in razdaljo. Polarni koordinatni sistem je še posebej uporaben, kadar je odnose med točkami lažje predstaviti kot razdalje in kote; v pogostejšem kartezičnem ali kartezičnem koordinatnem sistemu je takšne odnose mogoče vzpostaviti le z uporabo trigonometričnih enačb.
Polarni koordinatni sistem je podan z žarkom, ki ga imenujemo ničelna ali polarna os. Točka, iz katere izhaja ta žarek, se imenuje izhodišče ali pol. Vsaka točka na ravnini je določena z dvema polarnima koordinatama: radialno in kotno. Radialna koordinata (običajno označena r) ustreza razdalji od točke do izhodišča. Kotna koordinata, imenovana tudi polarni kot ali azimut in označena s φ, je enaka kotu, za katerega je treba polarno os zavrteti v nasprotni smeri urnega kazalca, da pridemo do te točke.
Tako določena radialna koordinata lahko zavzame vrednosti od nič do neskončnosti, kotna koordinata pa se spreminja od 0° do 360°. Vendar pa je zaradi udobja mogoče razpon vrednosti polarne koordinate razširiti preko celotnega kota, prav tako pa je mogoče dovoliti, da vzame negativne vrednosti, kar ustreza vrtenju polarne osi v smeri urinega kazalca.
3. Delitev segmentov v zvezi s tem.
Potrebno je razdeliti odsek AB, ki povezuje točki A(x1;y1) in B(x2;y2) v danem razmerju λ > 0, tj..jpg" align="left" width="84 height=84" height =" 84">
Rešitev: Upoštevajmo vektorja 15 src="> i.e. in i.e.
Enačba (9.1) ima obliko
Glede na to enaki vektorji imata enake koordinate, dobimo:
http://pandia.ru/text/78/214/images/image014_27.gif" width="56 height=28" height="28"> (9.2) in
http://pandia.ru/text/78/214/images/image016_26.gif" width="60 height=29" height="29"> (9,3)
Formuli (9.2) in (9.3) se imenujeta formule delitve segmentov v zvezi s tem. Zlasti za λ = 1, tj..gif" width="54" height="29 src=">. V tem primeru je točka M(x;y) sredini segmenta AB.
komentar:
Če je λ = 0, to pomeni, da točki A in M sovpadata, če je λ< 0, то точка Μ лежит вне отрезка АВ - говорят, что точка M делит отрезок АВ внешним образом , т. к. в противном случае , т. е. AM + MB = 0, т. е. АВ = 0).
4. Razdalja med točkami.
Najti je treba razdaljo d med točkama A(x1;y1) in B(x2;y2) na ravnini.
Rešitev: Želena razdalja d je enaka dolžini vektorja, tj. 
5. Enačba premice, ki poteka skozi dve točki.
Če sta na premici v prostoru označeni dve poljubni točki M1(x1, y1, z1) in M2(x2, y2, z2), potem morajo koordinate teh točk zadoščati zgoraj dobljeni enačbi premice:
Poleg tega lahko za točko M1 zapišemo:
Če rešimo te enačbe skupaj, dobimo:
.
To je enačba premice, ki poteka skozi dve točki v prostoru.
6. Determinante 2. reda.
Vrednost determinante 2. reda je enostavno izračunati po definiciji z uporabo formule.
7. Determinante 3. reda.
http://pandia.ru/text/78/214/images/image030_15.gif" width="120" height="61 src="> shema za izračun determinante po metodi trikotnika, tj.
http://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="183" height="73 src=">
Razmislite o sistemu treh linearnih enačb s tremi neznankami:
http://pandia.ru/text/78/214/images/image039_14.gif" width="79" height="46">.gif" width="264" height="48">.gif" width= "120" height="29">.gif" width="110" height="46 src=">
Razmislite o sistemski matriki in matričnih stolpcih neznanih in prostih členov
Poiščimo izdelek
http://pandia.ru/text/78/214/images/image049_13.gif" width="108" height="41"> ali krajše A∙X=B.
Tukaj so matrice A in B so znani, in matriko X neznano. Treba ga je najti, saj so njegovi elementi rešitev tega sistema. Ta enačba se imenuje matrična enačba.
Naj bo determinanta matrike drugačna od nič | A| ≠ 0. Potem se matrična enačba reši na naslednji način. Pomnožite obe strani enačbe na levi z matriko A-1, inverzna matrika A: http://pandia.ru/text/78/214/images/image051_13.gif" width="168" height="59"> 
Rešite naslednji sistem enačb na matričen način:
Pozor: ničle se pojavijo, če ni nobene spremenljivke, tj. če na primer X3 ni podan v pogoju, potem je samodejno enak nič. Enako z X1 in X2
http://pandia.ru/text/78/214/images/image057_9.gif" width="56 height=54" height="54">
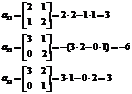
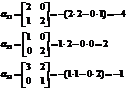
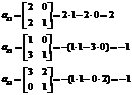
http://pandia.ru/text/78/214/images/image065_8.gif" width="160 height=51" height="51">
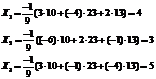odgovor:
# a) Glede na:
http://pandia.ru/text/78/214/images/image074_5.gif" width="59 height=16" height="16">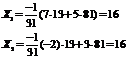 
odgovor:
http://pandia.ru/text/78/214/images/image081_5.gif" width="106" height="50 src=">
Poiščimo inverzno matriko.
Od vseh vrstic pod njo odštejte 1. vrstico. To dejanje ni v nasprotju z osnovnimi matričnimi transformacijami.
http://pandia.ru/text/78/214/images/image083_4.gif" width="172" height="52 src=">
Od vseh vrstic nad njo odštejte 3. vrstico. To dejanje ni v nasprotju z osnovnimi matričnimi transformacijami.
http://pandia.ru/text/78/214/images/image085_5.gif" width="187" height="53 src=">
Vse koeficiente na glavni diagonali matrike pripeljemo do 1. Vsako vrstico matrike razdelimo s koeficientom te vrstice, ki se nahaja na glavni diagonali, če ni enak 1. Kvadratna matrika, ki se je izkazala za desno od enotske matrike, je inverz glavne matrike.
http://pandia.ru/text/78/214/images/image087_4.gif" width="172" height="52 src=">
11. Vektorji. Seštevanje vektorjev.
http://www. bigpi. *****/encil/članki/15/1001553/1001553A. htm
Vektor imenujejo količino, za katero je značilna številčna vrednost, smer v prostoru in razvijanje z drugo, geometrijsko podobno vrednostjo.
Grafično so vektorji prikazani kot usmerjeni odseki črte določene dolžine, kot http://pandia.ru/text/78/214/images/image089_5.gif" width="17" height="17 src=">.jpg " alt= "(!LANG: vektorski dodatek a+b=b+a, a+(b+c)=(a+b)+c" width="110" height="46">!}
Izrek: Karkoli že so tri točke A, B in C, vektorska enakost velja
Ko je dodano dva vektorji pogosto uporabljajo tako imenovani " pravilo paralelograma". V tem primeru je paralelogram zgrajen z uporabo členov vektorjev kot njegovih sosednjih strani. Diagonala paralelograma, potegnjena iz točke, kjer sta povezana začetka vektorjev, je želena vsota (slika 4, levo).
Preprosto je videti (slika 4, desno), da to pravilo vodi do enakega rezultata kot zgornja metoda. Pri dodajanju več kot dveh vektorjev " pravilo paralelograma» se praktično ne uporablja zaradi okornih konstrukcij. Seštevanje vektorjev je komutativno, tj.
a + b = b + a.
In vendar vsota določenega števila vektorjev ni odvisna od vrstnega reda, v katerem so dodani, to je ( a + b) + d = a + (b + d). V tem primeru pravimo, da je seštevanje vektorjev asociativno, torej zanj velja asociativni zakon.
12. Skalarni produkt vektorjev.
http://www. dpva. info/Guide/GuideMathematics/linearAlgebra/ScalarVectorsMnoženje/
Pikasti produkt vektorjev je operacija na dveh vektorjih, ki ima za posledico število (ne vektor).
http://pandia.ru/text/78/214/images/image097_5.gif" width="86" height="23">
Z drugimi besedami, skalarni produkt vektorjev je enak produktu dolžin teh vektorjev in kosinusa kota med njimi. Upoštevati je treba, da je kot med dvema vektorjema kot, ki ga tvorita, če sta odložena iz ene točke, to pomeni, da se morata začetka vektorja ujemati.
Naslednje preproste lastnosti izhajajo neposredno iz definicije:
1. Skalarni produkt poljubnega vektorja a in samega sebe (skalarni kvadrat vektorja a) je vedno nenegativen in je enak kvadratu dolžine tega vektorja. Poleg tega je skalarni kvadrat vektorja enak nič, če in samo če je dani vektor enak nič.
2. Skalarni produkt poljubnih pravokotnih vektorjev a in b je enak nič.
3. Skalarni produkt dveh vektorjev je enak nič, če in samo če sta pravokotna ali je vsaj eden od njiju enak nič.
4. Skalarni produkt dveh vektorjev a in b je pozitiven, če in samo če je med njima oster kot.
5. Skalarni produkt dveh vektorjev a in b je negativen, če in samo če je med njima top kot.
Alternativna definicija skalarnega produkta ali izračun skalarnega produkta dveh vektorjev, podanih z njunima koordinatama.
(Zelo enostavno je izračunati koordinate vektorja glede na njegove začetne in končne koordinate.:
Naj obstaja vektor AB, A - začetek vektorja, B - konec in koordinate teh točk
A=(a1,a2,a3), B=(b1,b2,b3)
Potem koordinate vektorja AB:
AB=(b1-a1, b2-a2, b3-a3) .
Podobno v dvodimenzionalnem prostoru - tretjih koordinat preprosto ni)
Torej naj bosta dana dva vektorja, podana z nizom njunih koordinat:
a) V dvodimenzionalnem prostoru (na ravnini)..gif" width="49" height="19 src=">
Nato lahko njihov skalarni produkt izračunamo po formuli:
b) V tridimenzionalnem prostoru: ;
Podobno kot v dvodimenzionalnem primeru se njihov skalarni produkt izračuna po formuli:
http://pandia.ru/text/78/214/images/image103_3.gif" width="78" height="23 src=">.gif" width="98" height="24 src=">
Podobno izračunamo dolžino vektorja b.
pomeni, 
, 
Želeni kot je najden.
13. Vektorski izdelek.
http://www. dpva. info/Guide/GuideMathematics/linearAlgebra/vectorVectorsMultiplication/
Vektorski produkt dveh vektorjev a in b je operacija na njih, definirana le v tridimenzionalnem prostoru, katere rezultat je vektor z naslednjimi lastnostmi:
http://pandia.ru/text/78/214/images/image111_3.gif" width="83" height="27">, kjer a in b.
3) Vektor je usmerjen tako, da če pripeljete vektor http://pandia.ru/text/78/214/images/image117_3.gif" width="13" height="24 src=">. gif" width=" 13" height="24"> preden bo vektor v NASPROTNI SMERI URNEGA KAZALCA.
Za večjo jasnost navedimo primer - na sliki na desni je vektor - vektorski izdelek vektorja a in b. Kot je navedeno v definiciji, smo vse tri vektorje pripeljali do skupnega začetka, in potem, če pogledate vektorja a in b s konca vektorja, bo najkrajši obrat od vektorja a do vektorja b v nasprotni smeri urnega kazalca.
http://pandia.ru/text/78/214/images/image119_3.gif" width="76" height="25">
Prav tako neposredno iz definicije sledi, da za vsak skalarni faktor k (število) velja naslednje: 
det A http://pandia.ru/text/78/214/images/image182_2.gif" width="56 height=32" height="32">
7.2 Iskanje determinante matrike 3. reda po pravilu trikotnika
http://pandia.ru/text/78/214/images/image186_2.gif" width="132" height="45">
Vsakemu elementu kvadratne matrike (katerega vrstni red je večji ali enak tri) lahko pripišemo dve števili, imenovani MINOR ali ALGEBRAIČNI KOMPLEMENT. Minor elementa Aij kvadratne matrike A (poljubnega reda) je DETERMINANTA MATRIKE, ki jo dobimo iz matrike A z brisanjem vrstice in stolpca, v presečišču katerih stoji element Aij. Znak M - Manjša oznaka.
http://pandia.ru/text/78/214/images/image034_15.gif" width="72" height="51 src=">.gif" width="35" height="19">
http://pandia.ru/text/78/214/images/image194_1.gif" width="96 height=82" height="82">
ELEMENTI | Manjša | Algebrski komplement |
||||||||||||||||
Naj bo A \u003d neka matrika III reda, potem je determinanta matrike A enaka:
Opomba: determinanto je mogoče izračunati preko elementov kaj strune oz kaj stolpcev te matrike.
# Poiščite determinanto matrike po elementih prve vrstice in prvega stolpca:
http://pandia.ru/text/78/214/images/image201_0.gif" width="58" height="56 src=">
http://pandia.ru/text/78/214/images/image203_0.gif" width="253" height="34 src=">
7.3 determinanta matrike n-tega reda
Naj bo A kvadratna matrika reda n. Potem bo determinanta matrike n-tega reda videti takole:
Razširitev elementov 1 vrstice za iskanje elementov matrike A
http://pandia.ru/text/78/214/images/image206_0.gif" width="38" height="55">
6. Če se v določeni vrstici ali stolpcu determinante dodajo elementi druge vrstice ali stolpca, pomnoženi z istim številom, potem determinanta ne bo spremenila svoje vrednosti.
http://pandia.ru/text/78/214/images/image208_0.gif" width="48" height="12"> itd.
trikotni determinant- to je determinanta, za katero so vsi elementi, ki ležijo nad (ali pod) glavno diagonalo, ničle, enake produktu elementov glavne diagonale.
http://pandia.ru/text/78/214/images/image210_0.gif" width="37" height="28 src=">.gif" width="13 height=25" height="25"> )
Označimo ∆ =det A. Da ima kvadratna matrika A inverz, je potrebno in zadostuje, da je matrika nedegenerirana (razen nič). Inverz matrike A je označen z A-1, torej je B = A-1. Inverzna matrika se izračuna po formuli: C p - razdalja od izhodišča do ravnine.
http://pandia.ru/text/78/214/images/image248.gif" width="110" height="36 src=">
Tukaj je http://pandia.ru/text/78/214/images/image250.gif" width="29" height="13"> poljubno, če D=0.
21. Krivulje 2. (enačba krožnice).
Opredelitev 11.1.Krivulje drugega reda na ravnini se imenujejo presečišča krožnega stožca z ravninami, ki ne potekajo skozi njegov vrh.
Če taka ravnina seka vse generatorje ene votline stožca, potem se v odseku izkaže elipsa, na presečišču generatorjev obeh votlin - hiperbola, in če je sekalna ravnina vzporedna s katero koli generatriso, potem je odsek stožca parabola.
Komentiraj. Vse krivulje drugega reda so podane z enačbami druge stopnje v dveh spremenljivkah.
Klasifikacija krivulj drugega reda
Nedegenerirane krivulje
nedegeneriranče se lahko pojavijo naslednje možnosti:
Nedegenerirana krivulja drugi red se imenuje centralni, če
elipsa - priložena D> 0 in ∆ jaz < 0;
podan poseben primer elipse - krog jaz 2 = 4D oz a 11 = a 22,a 12 = 0;
namišljena elipsa (brez realne točke) - predmet Δ jaz > 0;
hiperbola - predmet D < 0;
Nedegenerirana krivulja drugega reda se imenuje necentralna, če je Δ jaz = 0
parabola - predmet D = 0.
Degenerirane krivulje: Krivulja drugega reda se imenuje degeneriranče je Δ = 0. Lahko se pojavijo naslednje možnosti:
realna točka na presečišču dveh namišljenih premic (degenerirana elipsa) – pod pogojem D > 0;
par pravih sekajočih se premic (degenerirana hiperbola) – pod pogojem D < 0;
degenerirana parabola – pod pogojem D = 0:
par pravih vzporednih premic – pod pogojem B < 0;
ena realna premica (dve združeni vzporedni premici) – pod pogojem B = 0;
par namišljenih vzporednih črt (brez ene prave točke) – priloženo B > 0.
22. Elipsa in njena enačba.
Opredelitev 11.2.Elipsa je množica točk v ravnini, za katere je vsota razdalj do dveh fiksnih točk F 1 in F 2 tega letala, imenovanega triki, je konstantna vrednost.
Komentiraj. Ko se točke poklopijo F 1 in F 2 se elipsa spremeni v krog.
Enačbo elipse izpeljemo z izbiro kartezičnega sistema: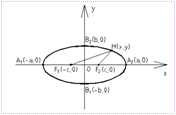 
koordinira tako, da os Oh sovpadal s črto F 1F 2, izvor koordinat - s sredino segmenta F 1F 2.
Naj bo dolžina tega segmenta 2 z, nato v izbranem koordinatnem sistemu F 1(-c, 0), F 2(c, 0). Naj bistvo M(x, y) leži na elipsi, vsota razdalj od nje do F 1 in F 2 je enako 2 a.
Potem r 1 + r 2 =2a, ampak http://pandia.ru/text/78/214/images/image255.gif" width="103" height="25 src="> ,
Zato http://pandia.ru/text/78/214/images/image257.gif" width="60" height="35 src="> (11.1)
Opredelitev 11.3.ekscentričnost elipso imenujemo kvantiteta e=c/a (11.2)
Opredelitev 11.4.Ravnateljica Di elipsa, ki ustreza fokusu fi, se imenuje ravna črta, ki se nahaja v isti polravnini z fi o osi OU pravokotno na os Oh na daljavo a/e od izvora.
Komentiraj. Z drugačno izbiro koordinatnega sistema je mogoče elipso podati ne s kanonično enačbo (11.1), ampak z drugačno enačbo druge stopnje.
Lastnosti elipse:
1) Elipsa ima dve medsebojno pravokotni simetrijski osi (glavni osi elipse) in simetrijsko središče (središče elipse). Če je elipsa podana s kanonično enačbo, potem so njene glavne osi koordinatne osi, središče pa izhodišče. Ker so dolžine segmentov, ki jih tvori presečišče elipse z glavnimi osmi, enake 2 a in 2 b (2a>2b), potem se glavna os, ki gre skozi žarišča, imenuje velika os elipse, druga velika os pa mala os.
2) Celotna elipsa je v pravokotniku http://pandia.ru/text/78/214/images/image029_18.gif" width="12" height="19 src=">
3) Ekscentričnost elipse e< 1.
Hiperbola.Opredelitev 11.5.Hiperbola je množica točk v ravnini, za katere je modul razlike med razdaljama do dveh fiksnih točk F 1 in F 2 tega letala, imenovanega triki, je konstantna vrednost.http://pandia.ru/text/78/214/images/image265.gif" width="180" height="29">. b² = c² - a², tukaj lahko dobite http://pandia.ru/text/78/214/images/image267.gif" width="38" height="30 src=">.gif" width="87" height= "44 src="> , (11.3`)
pri katerem se realne in imaginarne osi zamenjajo, pri čemer se ohranijo iste asimptote.
4) Ekscentričnost hiperbole e> 1.
5) Razmerje razdalje ri hiperbolična točka za fokus fi na daljavo di od te točke do direktrise, ki ustreza gorišču, je enaka ekscentričnosti hiperbole.
Dokaz lahko izvedemo na enak način kot za elipso.
23. Parabola.
Opredelitev 11.8.parabola je množica točk v ravnini, za katere je razdalja do neke fiksne točke F ta ravnina je enaka razdalji do neke fiksne premice. Pika F klical fokus parabole in ravna črta - njena ravnateljica.
Za izpeljavo enačbe parabole izberemo kartezični koordinatni sistem tako, da je njegovo izhodišče središče navpičnice FD, spuščeno iz gorišča na direktriso, koordinatne osi pa so bile vzporedne in pravokotne na direktriso. Naj dolžina segmenta FD
D O F x je R. Potem iz enakosti r = d iz tega sledi, da http://pandia.ru/text/78/214/images/image271.gif" width="101 height=38" height="38">,
Z algebrskimi transformacijami lahko to enačbo reduciramo na obliko:
l² = 2 px, (11.4) imenovano kanonična enačba parabole.
Vrednost R klical parameter parabole.
Lastnosti parabole :
1) Parabola ima simetrijsko os (os parabole). Točka presečišča parabole z osjo se imenuje vrh parabole. Če je parabola podana s kanonično enačbo, potem je njena os os Oh, in vrh je izhodišče koordinat.
2) Celotna parabola se nahaja v desni polravnini ravnine Ohu.
Komentiraj. Z uporabo lastnosti direktris elipse in hiperbole ter definicije parabole lahko dokažemo naslednjo trditev:
Množica ravninskih točk, za katere je razmerje e razdalja do neke fiksne točke do razdalje do neke ravne črte je konstantna vrednost, je elipsa (z e<1), гиперболу (при e>1) ali parabolo (ko e=1).
Redukcija enačbe drugega reda na kanonično obliko.
Opredelitev 11.9. Premica, definirana s splošno enačbo drugega reda
http://pandia.ru/text/78/214/images/image274.gif" width="103 height=19" height="19"> lahko nastavite matriko
http://pandia.ru/text/78/214/images/image276.gif" width="204" height="24 src="> (ob predpostavki, da λ 1,2 nista enaka 0).
Zastavimo kasnejši vzporedni prenos po formulah: , .
Dobimo ga v novem koordinatni sistem enačba. (11,7)
Razmislite o možnih geometrijskih slikah, ki jih določa ta enačba glede na znake λ
Pravokotni koordinatni sistem v prostoru tvorijo tri med seboj pravokotne koordinatne osi OX, ojoj in oz. Koordinatni osi se sekata v točki O, ki se imenuje izhodišče koordinat, je na vsaki osi izbrana pozitivna smer, označena s puščicami, in merska enota segmentov na oseh. Merske enote so običajno enake za vse osi (kar ni obvezno). OX- abscisna os, ojoj- y-os, oz- os aplikacije.
Če za smer vzamemo palec desne roke X, ki kaže smer Y, in povprečje na smer Z, potem se oblikuje prav koordinatni sistem. Podobni prsti leve roke tvorijo levi koordinatni sistem. Z drugimi besedami, pozitivna smer osi je izbrana tako, da ko se os vrti OX v nasprotni smeri urinega kazalca za 90° je njegova pozitivna smer sovpadala s pozitivno smerjo osi ojoj, če to vrtenje opazujemo s strani pozitivne smeri osi oz. Desnega in levega koordinatnega sistema ni mogoče kombinirati tako, da bi ustrezni osi sovpadali (glej sliko 2).
Položaj točke A v prostoru določajo tri koordinate x, l in z. Koordinate x enaka dolžini segmenta OB, koordiniraj l- dolžina segmenta OC, koordiniraj z- dolžina segmenta OD v izbranih merskih enotah. Segmenti OB, OC in OD definirajo ravnine, ki potekajo iz točke A vzporedno z ravninami YOZ, XOZ in XOY oz. Koordinate x imenujemo abscisa točke A, koordiniraj l- ordinatna točka A, koordiniraj z- točka nanosa A. Zapišejo takole:
