Diferencialne enačbe 2. reda
§ena. Metode za znižanje reda enačbe.
Diferencialna enačba 2. reda ima obliko:
http://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="119" height="25 src="> ( ali Differential" href="/text/category/differentcial/" rel="bookmark"> diferencialna enačba 2. naročilo). Cauchyjev problem za diferencialno enačbo 2. reda (1..gif" width="85" height="25 src=">.gif" width="85" height="25 src=">.gif" height=" 25 src =">.
Naj bo diferencialna enačba 2. reda videti takole: http://pandia.ru/text/78/516/images/image009_41.gif" height="25 src=">..gif" width="39" height=" 25 src=">.gif" width="265" height="28 src=">.
Tako je enačba 2. reda http://pandia.ru/text/78/516/images/image015_28.gif" width="34" height="25 src=">.gif" width="118" height =" 25 src=">.gif" width="117" height="25 src=">.gif" width="34" height="25 src=">. Če jo rešimo, dobimo splošni integral izvirne diferencialne enačbe, ki je odvisna od dveh poljubnih konstant: http://pandia.ru/text/78/516/images/image020_23.gif" width="95" height="25 src=">. gif" width="76" height="25 src=">.
Rešitev.
Ker v prvotni enačbi ni eksplicitnega argumenta http://pandia.ru/text/78/516/images/image011_39.gif" height="25 src=">.gif" width="35" height="25 src=">..gif" width="35" height="25 src=">.gif" width="82" height="38 src="> ..gif" width="99" height="38 src=">.
Od http://pandia.ru/text/78/516/images/image029_18.gif" width="85" height="25 src=">.gif" width="42" height="38 src= " >.gif" width="34" height="25 src=">.gif" width="68" height="35 src=">..gif" height="25 src=">.
Naj bo diferencialna enačba 2. reda videti takole: http://pandia.ru/text/78/516/images/image011_39.gif" height="25 src=">..gif" width="161" height=" 25 src=">.gif" width="34" height="25 src=">.gif" width="33" height="25 src=">..gif" width="225" height="25 src =">..gif" width="150" height="25 src=">.
Primer 2 Poiščite splošno rešitev enačbe: http://pandia.ru/text/78/516/images/image015_28.gif" width="34" height="25 src=">.gif" width="107" height ="25 src=">..gif" width="100" height="27 src=">.gif" width="130" height="37 src=">.gif" width="34" height= "25 src =">.gif" width="183" height="36 src=">.
3. Vrstni red stopnje se zmanjša, če ga je mogoče preoblikovati v takšno obliko, da oba dela enačbe postaneta skupni derivat http://pandia.ru/text/78/516/images/image052_13.gif" širina="92" višina="25 src=">..gif" širina="98" višina="48 src=">.gif" širina="138" višina="25 src=">.gif" širina ="282" višina="25 src=">, (2.1)
kjer http://pandia.ru/text/78/516/images/image060_12.gif" width="42" height="25 src=">.gif" width="42" height="25 src="> so podane funkcije, ki so zvezne na intervalu, na katerem iščemo rešitev. Ob predpostavki, da je a0(x) ≠ 0, delite z (2..gif" width="215" height="25 src="> (2.2)
Predpostavimo brez dokaza, da (2..gif" width="82" height="25 src=">.gif" width="38" height="25 src=">.gif" width="65" height= " 25 src=">, potem enačbo (2.2) imenujemo homogena, enačbo (2.2) pa nehomogeno drugače.
Oglejmo si lastnosti rešitev lodu 2. reda.
Opredelitev. Linearna kombinacija funkcij http://pandia.ru/text/78/516/images/image071_10.gif" width="93" height="25 src=">.gif" width="42" height="25 src = ">.gif" width="195" height="25 src=">, (2.3)
nato njihovo linearno kombinacijo http://pandia.ru/text/78/516/images/image076_10.gif" width="182" height="25 src="> v (2.3) in pokažite, da je rezultat identiteta:
http://pandia.ru/text/78/516/images/image078_10.gif" width="368" height="25 src=">.
Ker so funkcije http://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> rešitve enačbe (2.3), potem je vsak oklepaj v zadnja enačba je identično enaka nič, kar je bilo treba dokazati.
Posledica 1. Iz dokazanega izreka sledi, ko je http://pandia.ru/text/78/516/images/image080_10.gif" width="77" height="25 src="> rešitev enačbe (2.3), potem DIV_ADBLOCK101">
Posledica 2. Predpostavka http://pandia.ru/text/78/516/images/image083_11.gif" width="58" height="25 src="> je tudi rešitev te enačbe.
Komentiraj. Lastnost rešitev, dokazana v izreku, ostane veljavna za primer katerega koli reda.
§3. Določnik Vronskega.
Opredelitev. Sistem funkcij http://pandia.ru/text/78/516/images/image084_10.gif" width="61" height="25 src=">.gif" width="110" height="47 src= " >..gif" width="106" height="42 src=">..gif" width="42" height="25 src=">.gif" width="181" height="47 src= " >.gif" width="42" height="25 src="> enačbe (2.3)..gif" width="182" height="25 src=">. (3.1)
Dejansko ..gif" width="18" height="25 src="> izpolnjuje enačbo (2..gif" width="42" height="25 src="> je rešitev enačbe (3.1). .gif" width="87" height="28 src=">..gif" width="182" height="34 src=">..gif" width="162" height="42 src="> .gif" width="51" height="25 src="> je enak. Tako
http://pandia.ru/text/78/516/images/image107_7.gif" width="18" height="25 src=">, v kateri je determinanta za linearno neodvisne rešitve enačbe (2..gif " width= "42" height="25 src=">.gif" height="25 src="> Oba faktorja na desni strani formule (3.2) sta različna od nič.
§ štiri. Struktura splošne rešitve lod. 2. reda.
Izrek.Če so http://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> linearno neodvisne rešitve enačbe (2..gif" width=" 19" height="25 src=">.gif" width="129" height="25 src=">je rešitev enačbe (2.3), izhaja iz izreka o lastnostih lodujevih rešitev 2. reda..gif " width="85 "height="25 src=">.gif" width="19" height="25 src=">.gif" width="220" height="47">
Konstante http://pandia.ru/text/78/516/images/image003_79.gif" width="19" height="25 src="> iz tega sistema linearnih algebrskih enačb so enolično določene, saj je determinanta ta sistem http: //pandia.ru/text/78/516/images/image006_56.gif" width="51" height="25 src=">:
http://pandia.ru/text/78/516/images/image116_7.gif" width="138" height="25 src=">.gif" width="19" height="25 src=">. gif" width="69" height="25 src=">.gif" width="235" height="48 src=">..gif" width="143" height="25 src="> (5 ..gif" width="77" height="25 src=">. Glede na prejšnji odstavek je splošno rešitev lodu 2. reda enostavno določiti, če sta znani dve linearno neodvisni delni rešitvi te enačbe. Preprosta metoda za iskanje delnih rešitev enačbe s konstantnimi koeficienti, ki jih je predlagal L. Euler..gif" width="25" height="26 src=">, dobimo algebraično enačbo, ki ji pravimo karakteristika:
http://pandia.ru/text/78/516/images/image124_5.gif" width="59" height="26 src="> bo rešitev enačbe (5.1) samo za tiste vrednosti k ki so korenine karakteristične enačbe (5.2)..gif" width="49" height="25 src=">..gif" width="76" height="28 src=">.gif" width= "205" height="47 src ="> in splošna rešitev (5..gif" width="45" height="25 src=">..gif" width="74" height="26 src=" >..gif" width="83 " height="26 src=">. Preverite, ali ta funkcija ustreza enačbi (5.1)..gif" width="190" height="26 src=">. Zamenjava teh izrazov v enačbo (5.1), dobimo
http://pandia.ru/text/78/516/images/image141_6.gif" width="328" height="26 src=">, because.gif" width="137" height="26 src=" >.
Zasebne rešitve http://pandia.ru/text/78/516/images/image145_6.gif" width="86" height="28 src="> so linearno neodvisne, saj.gif" width="166" height= "26 src=">.gif" width="45" height="25 src=">..gif" width="65" height="33 src=">.gif" width="134" height =" 25 src=">.gif" width="267" height="25 src=">.gif" width="474" height="25 src=">.
Oba oklepaja na levi strani te enakosti sta identično enaka nič..gif" width="174" height="25 src=">..gif" width="132" height="25 src="> je rešitev enačbe (5.1) ..gif" width="129" height="25 src="> bo videti takole:
http://pandia.ru/text/78/516/images/image162_6.gif" width="179" height="25 src="> f(x) (6,1)
predstavljen kot vsota celotne rešitve DIV_ADBLOCK103">
http://pandia.ru/text/78/516/images/image165_6.gif" width="11" height="29 src="> lndu (6.1).
Dokaz.
Najprej dokažimo, da http://pandia.ru/text/78/516/images/image166_6.gif" width="87" height="25 src="> v enačbo (6..gif" width=" 156" height="25 src=">.gif" width="87" height="25 src="> je rešitev enačbe (6.1).
Dokažimo zdaj, da je ta rešitev splošna, tj. da lahko vanjo vključimo poljubne konstante tako, da bodo izpolnjeni kateri koli začetni pogoji oblike: http://pandia.ru/text/78/516/images /image170_5.gif" width="91" height="25 src="> (6.3). Po izreku o zgradbi splošne rešitve linearne homogene diferencialne enačbe (lodu) je splošna rešitev enačbe ( 6..gif" width="17" height="25 src= ">.gif" width="160" height="25 src="> in zato lahko začetne pogoje (6.3) zapišemo kot:
http://pandia.ru/text/78/516/images/image174_4.gif" width="289" height="48 src="> (6,4)
Poljubne konstante http://pandia.ru/text/78/516/images/image003_79.gif" width="19" height="25 src="> so enolično določene iz tega sistema linearnih algebrskih enačb za katero koli desno stran, tj. k..gif" width="133" height="47 src="> je vrednost determinante Wronsky za linearno neodvisne rešitve enačbe (6..gif" width="19" height="25 src=">.gif" width ="160" height="25 src=">, dobimo partikularno rešitev enačbe (6.1), ki zadošča danim začetnim pogojem. Izrek je dokazan.
Dokažimo še en preprost izrek, ki se pogosto uporablja pri reševanju problemov.
2. izrek.Če http://pandia.ru/text/78/516/images/image162_6.gif" width="179" height="25 src=">.gif" width="179" height="25 src="> .gif" width="179" height="25 src="> f1(x) + f2(x). (6.5)
Dokaz.
Zamenjava funkcije http://pandia.ru/text/78/516/images/image180_5.gif" width="284" height="25 src="> f1 + f2. Ta enakost je identiteta, ker.gif " width="141" height="25 src="> f2. Izrek je dokazan.
§7. Rešitev problema 2. reda s konstantnimi koeficienti s posebno desno stranjo.
Naj bodo koeficienti v enačbi (6.1) konstantni, tj. enačba ima obliko:
http://pandia.ru/text/78/516/images/image184_5.gif" width="95" height="25 src=">.
Razmislite o metodi iskanja določene rešitve http://pandia.ru/text/78/516/images/image186_5.gif" width="109" height="25 src=">.gif" width="16" height ="25 src=">.gif" width="11" height="25 src="> ni koren karakteristične enačbe za enačbo (5..gif" width="131" height="25 src ="> – nedefinirani koeficienti, ki jih je treba določiti z metodo nedoločenih koeficientov.
Primer 1 Poiščite splošno rešitev enačbe http://pandia.ru/text/78/516/images/image194_5.gif" width="85" height="25 src=">.gif" width="48" height= "25 src =">.gif" width="207" height="25 src=">..gif" width="45" height="25 src=">.gif" width="30" height=" 25 src= "> - nedoločeni koeficienti. Poiščite odvode prvega in drugega reda in jih nadomestite v dano enačbo:
http://pandia.ru/text/78/516/images/image204_5.gif" width="25" height="25 src="> in izenačite koeficiente na enakih stopnjah v levem in desnem delu enakosti
Diferencialna enačba drugega reda povezuje neodvisno spremenljivko, želeno funkcijo ter njen prvi in drugi odvod. V posebnih primerih lahko enačba manjka. Vendar pa mora enačba drugega reda vsebovati .
Diferencialna enačba drugega reda je na splošno zapisana kot
ali, če je mogoče, v obliki, ki je dovoljena glede na drugo izpeljanko
![]()
V 1. točki 1. odstavka smo obravnavali problem, ki je pripeljal do najpreprostejše diferencialne enačbe drugega reda (glej formulo 4. 1. odstavka, 1. točka).
Kot v primeru enačbe prvega reda obstaja tudi za enačbo drugega reda splošna in posebna rešitev. Najprej na primeru razmislimo, kakšno obliko ima splošna rešitev enačbe drugega reda in kako se iz nje izlušči določena rešitev.
Vzemimo najpreprostejšo enačbo drugega reda
Da bi jo rešili, uvedemo zapis. Takrat bo tudi enačba (35) dobila obliko . Iz tega sledi oz. S ponovnim integriranjem najdemo .
Dobljena rešitev je odvisna od dveh poljubnih konstant (splošna rešitev). Geometrijsko predstavlja ta rešitev množico parabol (integralnih krivulj), skozi vsako točko ravnine pa očitno poteka neskončno število parabol, ki imajo na tej točki različne tangente (slika 275). Za izbiro katere koli integralne krivulje iz nabora teh krivulj je potrebno poleg koordinat točke, skozi katero poteka parabola, dodatno nastaviti naklon tangente, tj. vrednost v tej točki odvoda
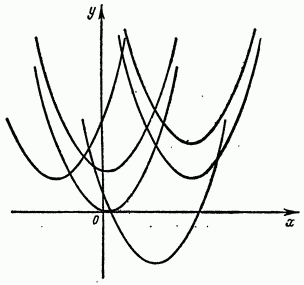
Tako imajo pogoji, s katerimi se določena rešitev (začetni pogoji) izluščijo iz splošne rešitve enačbe drugega reda, obliko:
![]()
Prvi od teh pogojev določa točko, skozi katero mora iti integralna krivulja. Drugi pogoj določa naklon integralne krivulje v dani točki.
Postavimo na primer naslednje začetne pogoje za enačbo (35): .
Iz splošne rešitve najdemo. Z uporabo začetnih pogojev dobimo za določitev sistema enačb
![]()
Iz tega sistema najdemo vrednosti. Zato ima želena partikularna rešitev obliko
Izobraževalna ustanova "Beloruska država
kmetijska akademija"
Oddelek za višjo matematiko
Smernice
o študiju teme "Linearne diferencialne enačbe drugega reda" študentov računovodskega oddelka dopisne oblike izobraževanja (NISPO)
Gorki, 2013
Linearne diferencialne enačbe
drugega reda s konstantokoeficientov
Linearne homogene diferencialne enačbe
Linearna diferencialna enačba drugega reda s konstantnimi koeficienti se imenuje enačba oblike
tiste. enačba, ki vsebuje želeno funkcijo in njene odvode samo do prve stopnje in ne vsebuje njihovih produktov. V tej enačbi 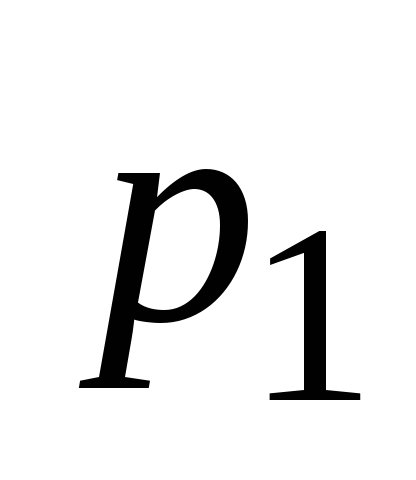 in
in 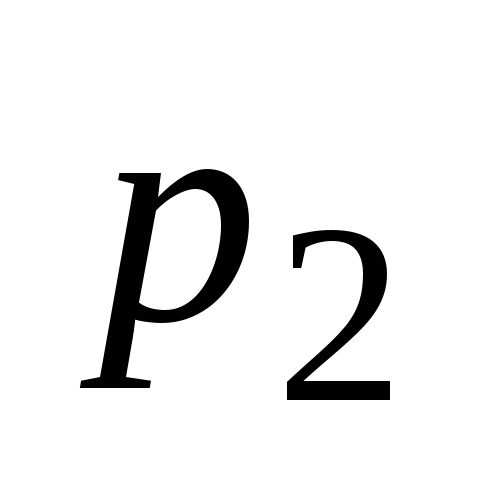 je nekaj števil in funkcija
je nekaj števil in funkcija 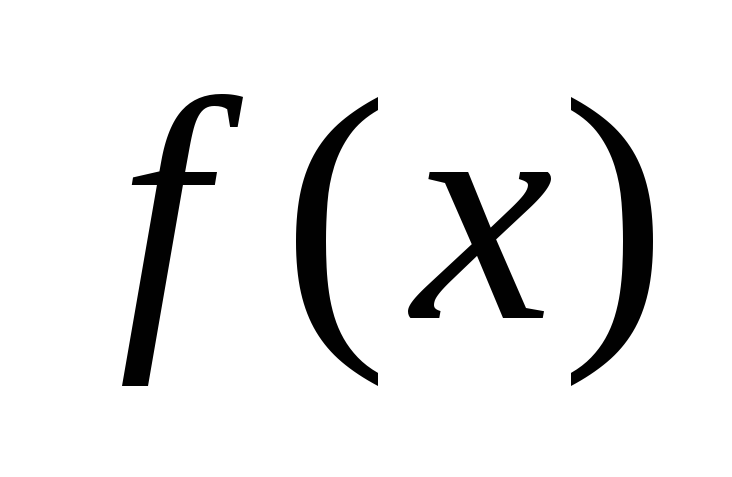 dano v nekem intervalu
dano v nekem intervalu 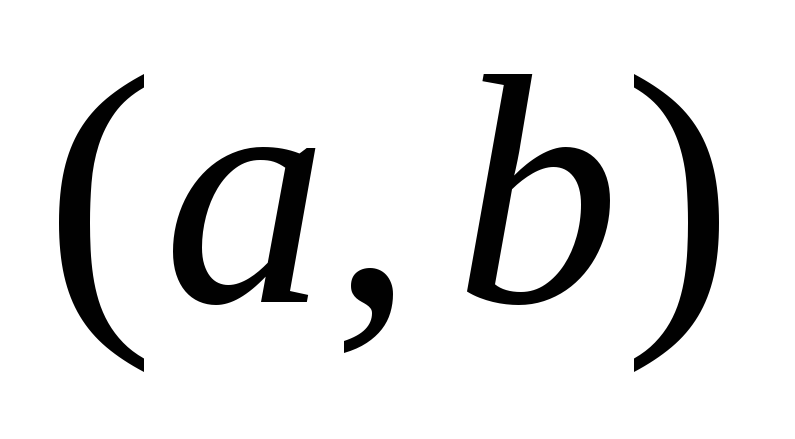 .
.
Če 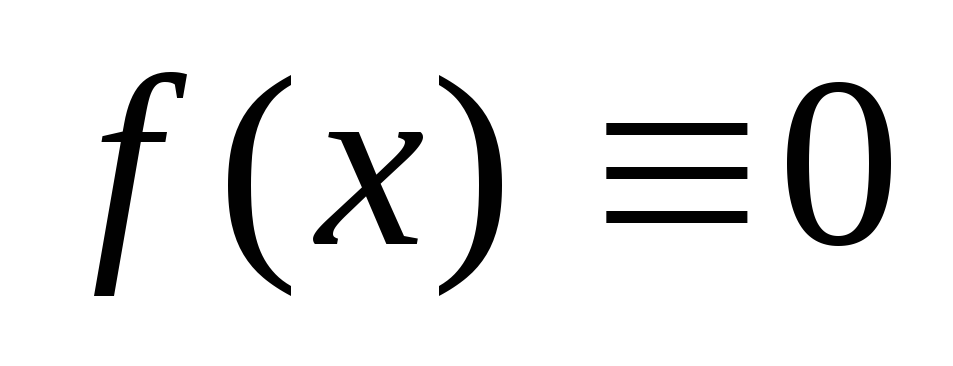 na intervalu
na intervalu 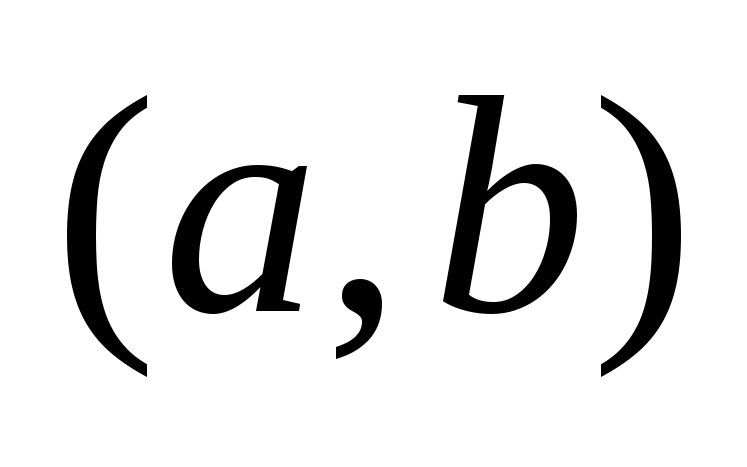 , potem ima enačba (1) obliko
, potem ima enačba (1) obliko
![]() ,
(2)
,
(2)
in poklical linearno homogena . V nasprotnem primeru se imenuje enačba (1). linearno nehomogena .
Razmislite o kompleksni funkciji
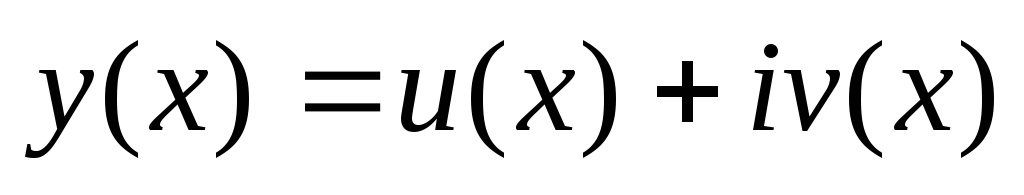 ,
(3)
,
(3)
kje 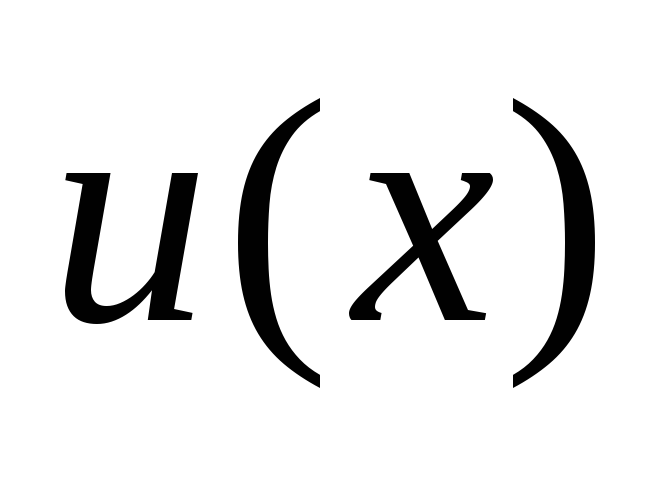 in
in 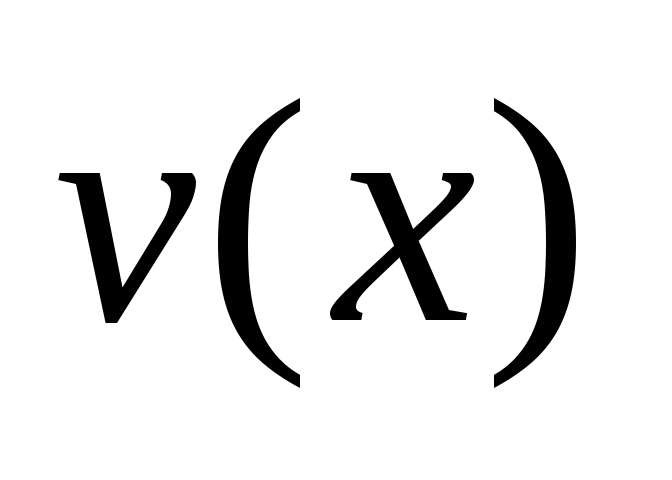 so prave funkcije. Če je funkcija (3) kompleksna rešitev enačbe (2), potem je realni del
so prave funkcije. Če je funkcija (3) kompleksna rešitev enačbe (2), potem je realni del 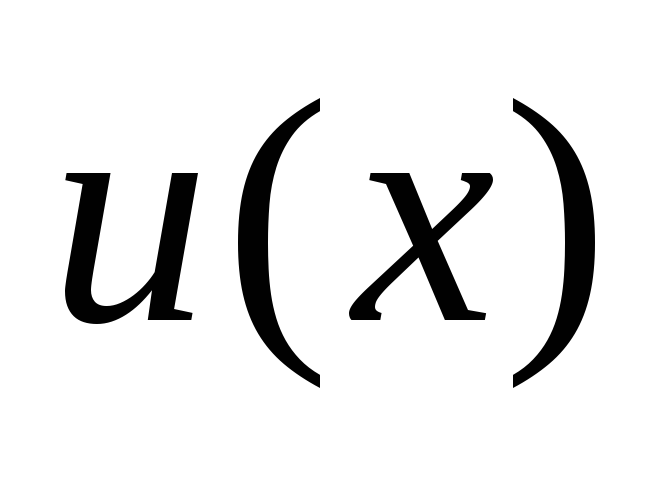 , in imaginarni del
, in imaginarni del 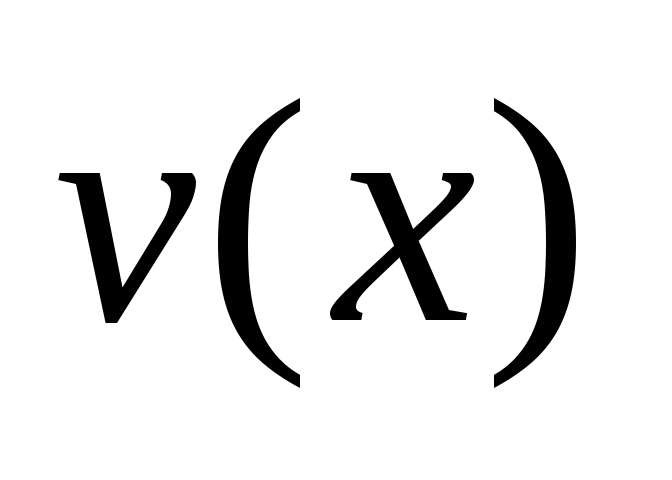 rešitve
rešitve 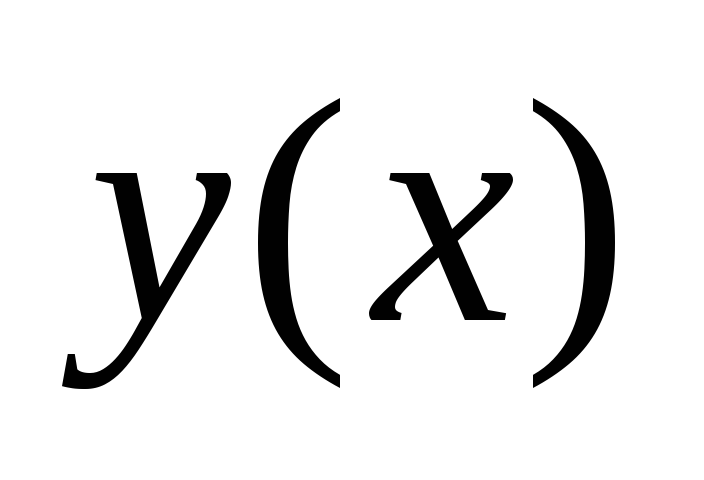 ločeno so rešitve iste homogene enačbe. Tako vsaka kompleksna rešitev enačbe (2) generira dve realni rešitvi te enačbe.
ločeno so rešitve iste homogene enačbe. Tako vsaka kompleksna rešitev enačbe (2) generira dve realni rešitvi te enačbe.
Rešitve homogene linearne enačbe imajo naslednje lastnosti:
 Če
Če 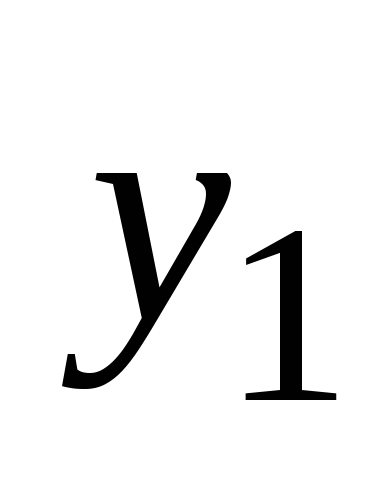 je rešitev enačbe (2), potem funkcija
je rešitev enačbe (2), potem funkcija 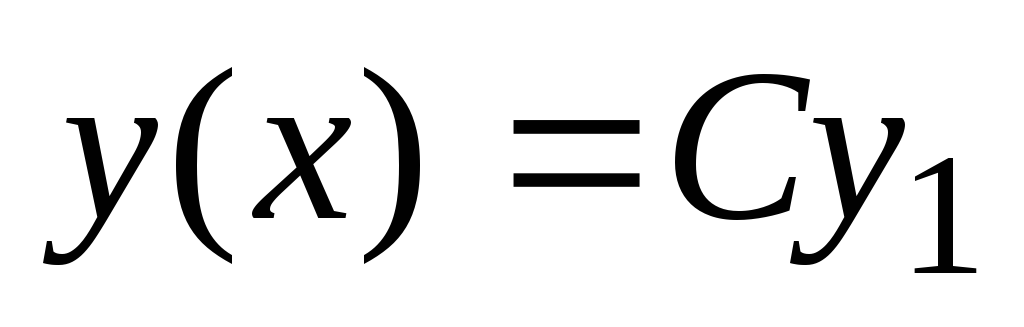 , kje OD- poljubna konstanta, bo tudi rešitev enačbe (2);
, kje OD- poljubna konstanta, bo tudi rešitev enačbe (2);
 Če
Če 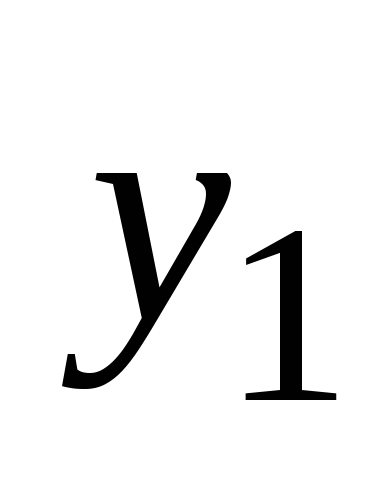 in
in 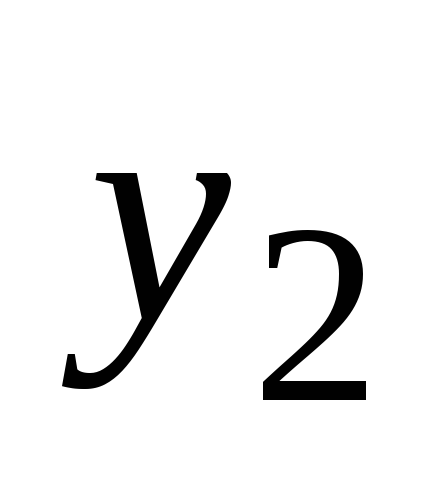 so rešitve enačbe (2), potem funkcija
so rešitve enačbe (2), potem funkcija 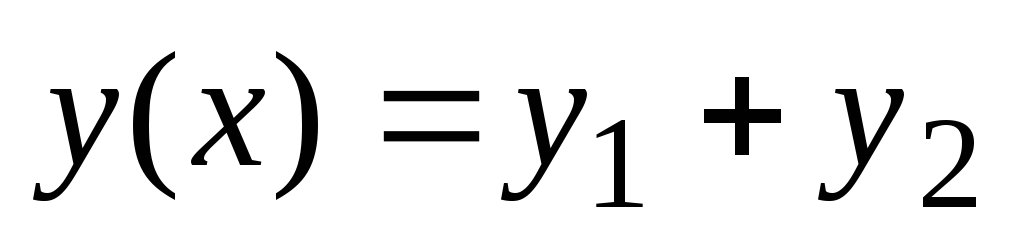 bo tudi rešitev enačbe (2);
bo tudi rešitev enačbe (2);
 Če
Če 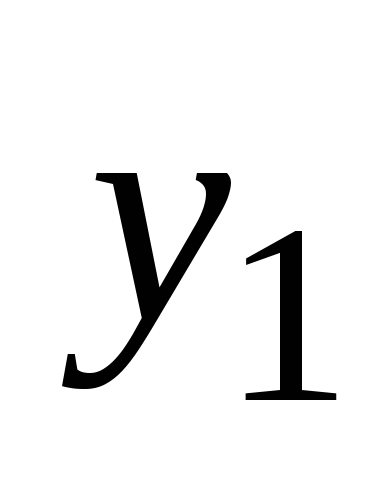 in
in 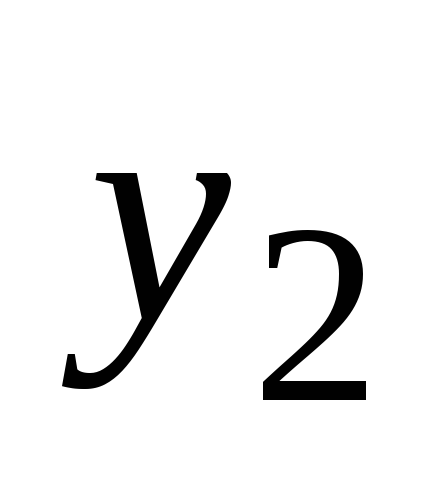 so rešitve enačbe (2), potem njihova linearna kombinacija
so rešitve enačbe (2), potem njihova linearna kombinacija 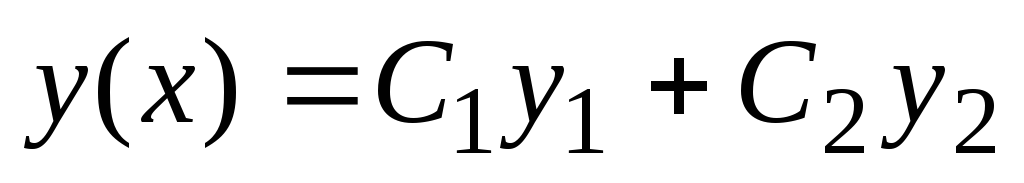 bo tudi rešitev enačbe (2), kjer
bo tudi rešitev enačbe (2), kjer 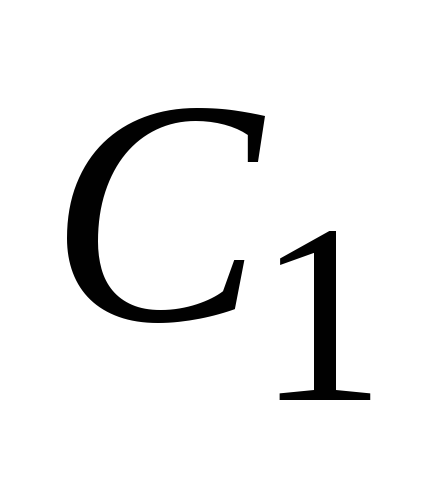 in
in 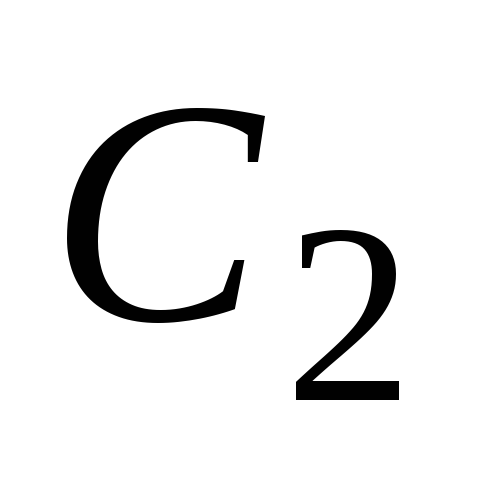 so poljubne konstante.
so poljubne konstante.
Funkcije 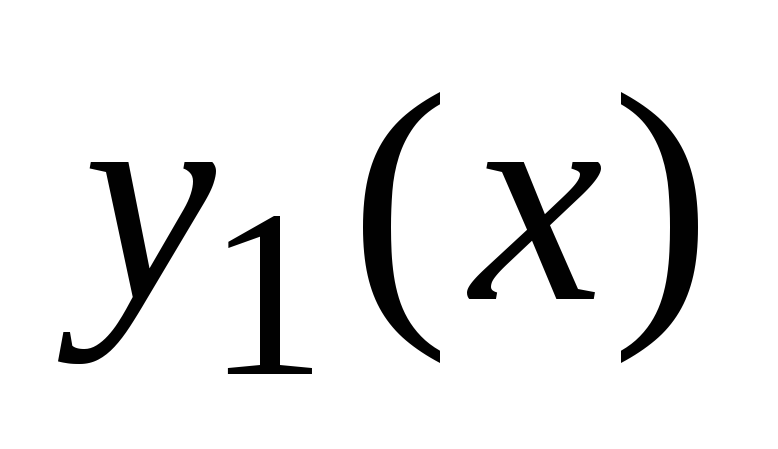 in
in 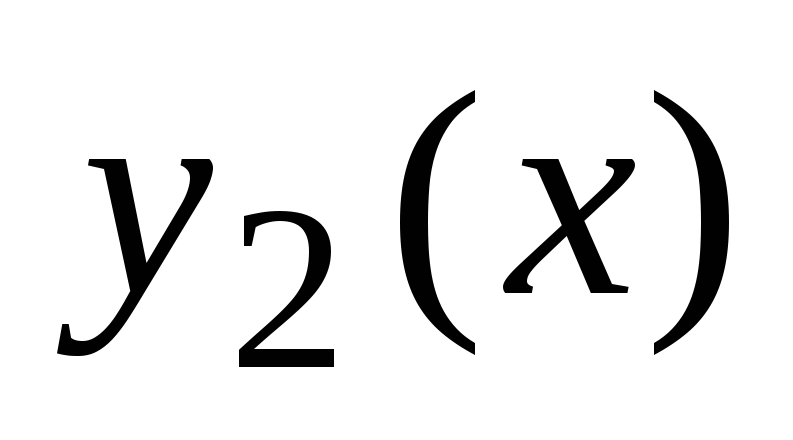 klical linearno odvisen
na intervalu
klical linearno odvisen
na intervalu 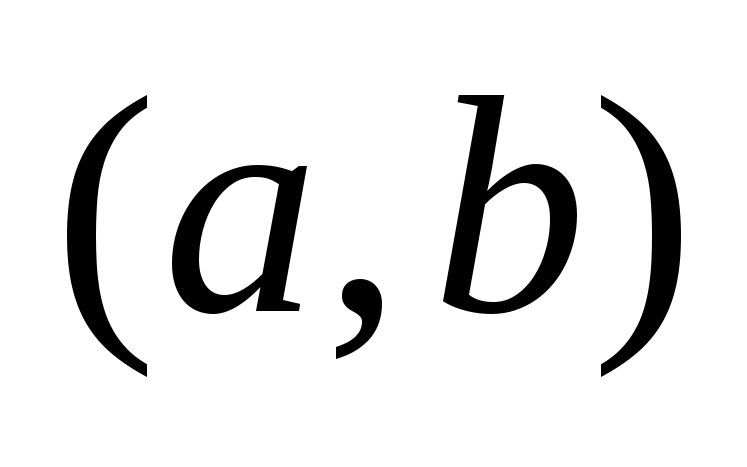 če obstajajo takšne številke
če obstajajo takšne številke 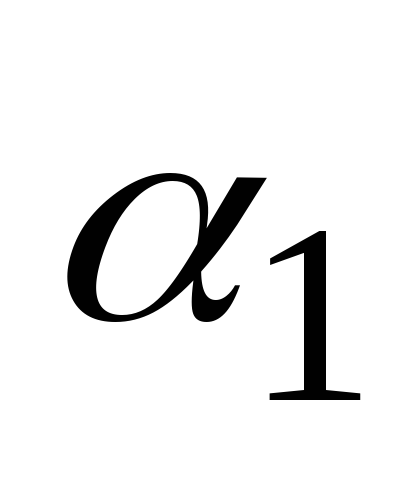 in
in 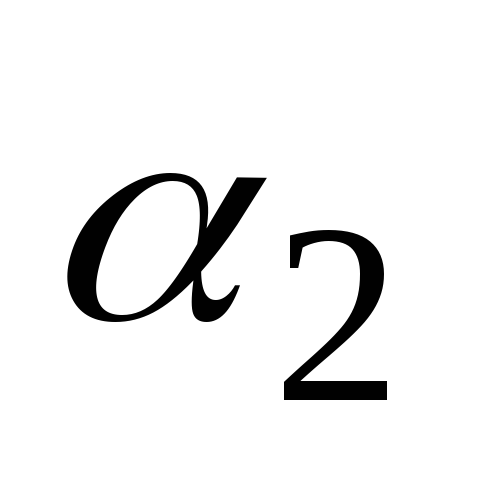 , ki hkrati nista enaka nič, da na tem intervalu velja enakost
, ki hkrati nista enaka nič, da na tem intervalu velja enakost
Če enakost (4) velja samo takrat, ko 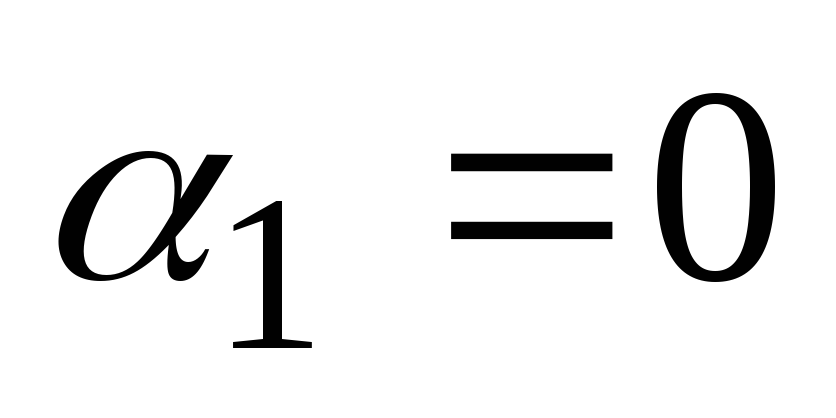 in
in 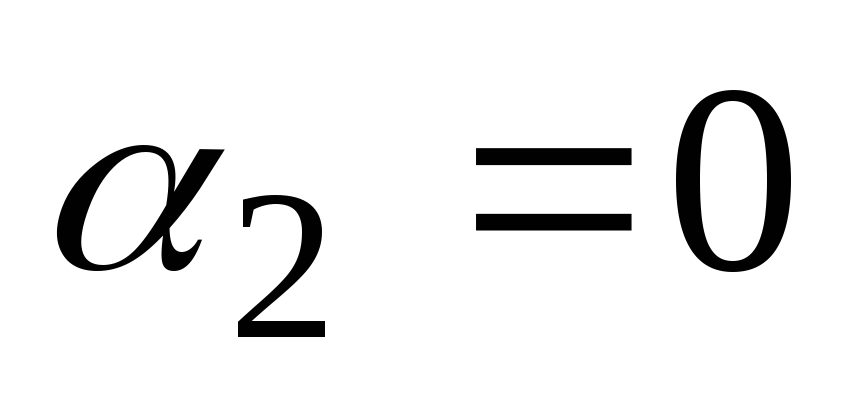 , nato funkcije
, nato funkcije 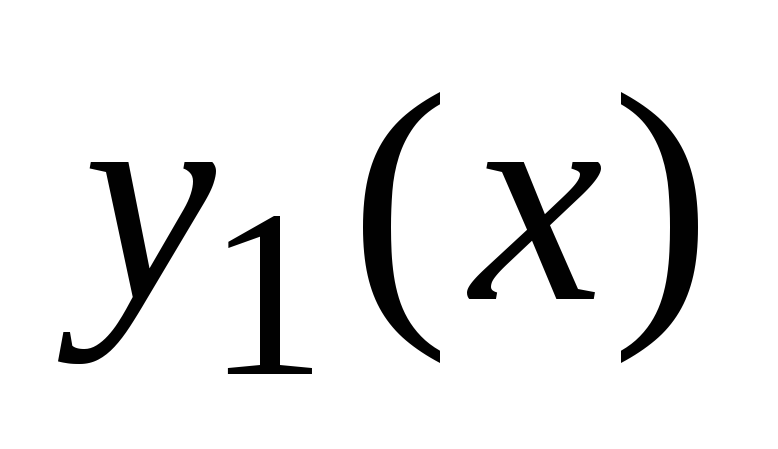 in
in 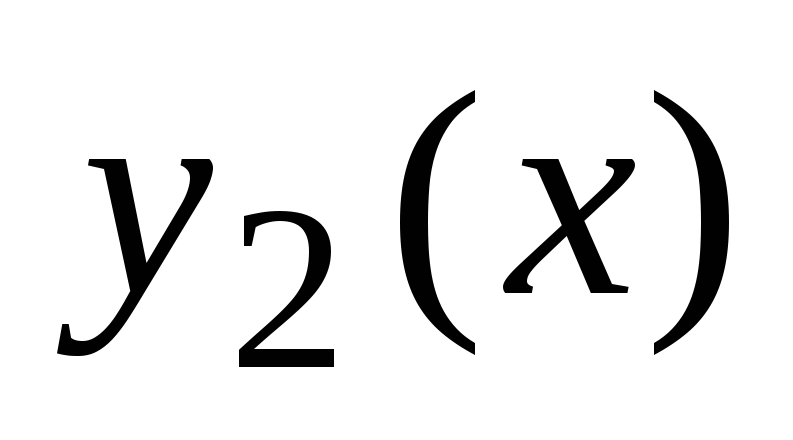 klical linearno neodvisen
na intervalu
klical linearno neodvisen
na intervalu 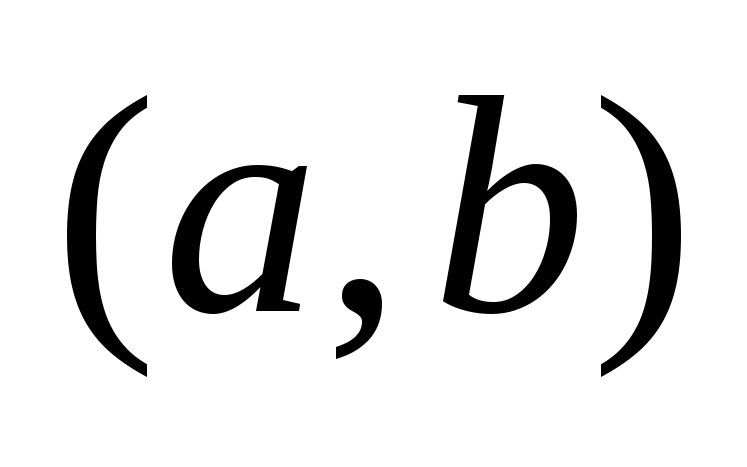 .
.
Primer 1
. Funkcije 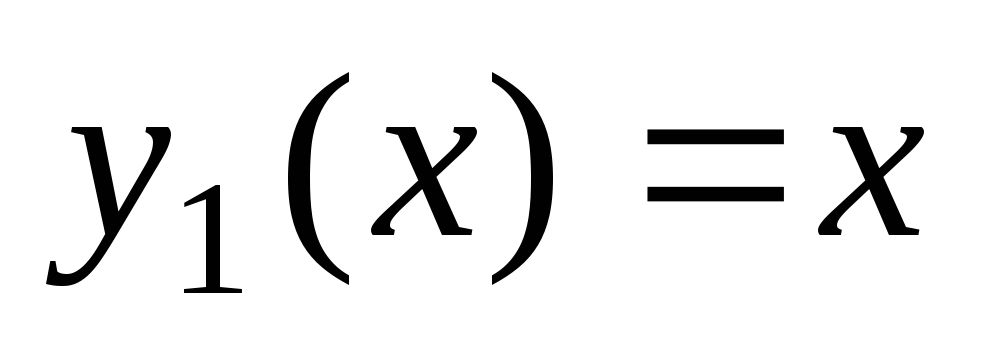 in
in 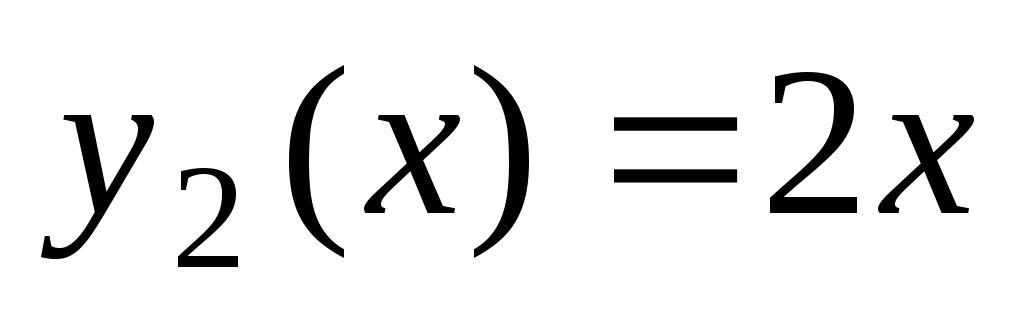 so linearno odvisni, saj
so linearno odvisni, saj 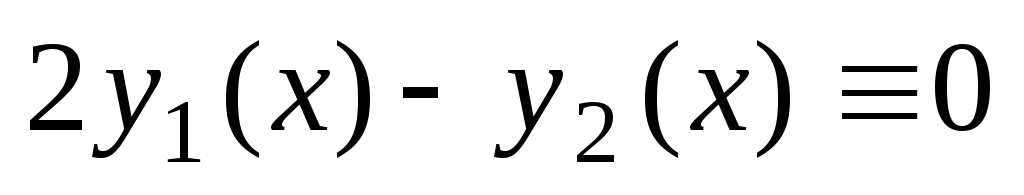 vzdolž celotne številske premice. V tem primeru
vzdolž celotne številske premice. V tem primeru 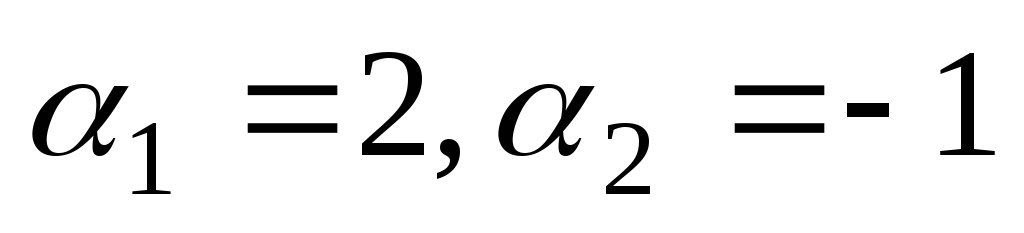 .
.
Primer 2
. Funkcije 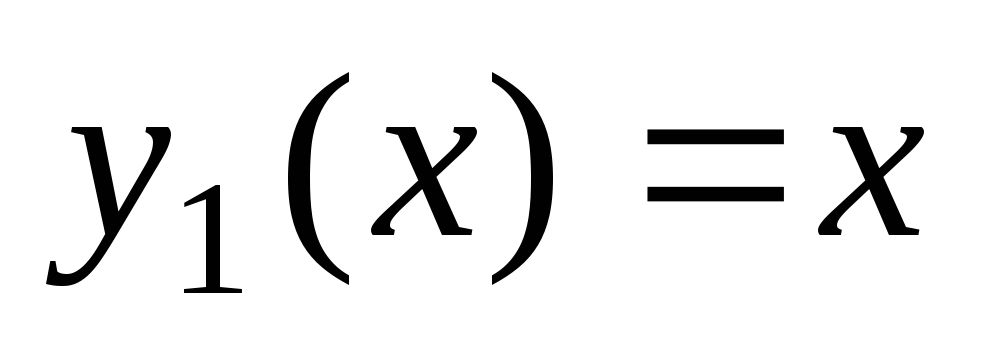 in
in 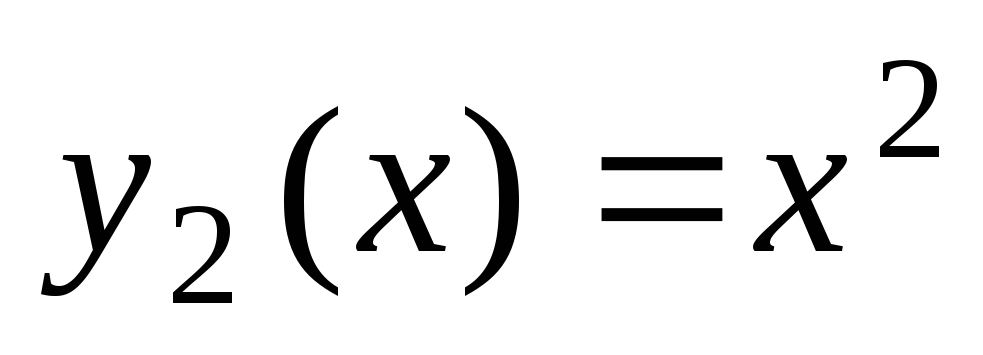 so linearno neodvisne na kateremkoli intervalu, saj velja enakost
so linearno neodvisne na kateremkoli intervalu, saj velja enakost 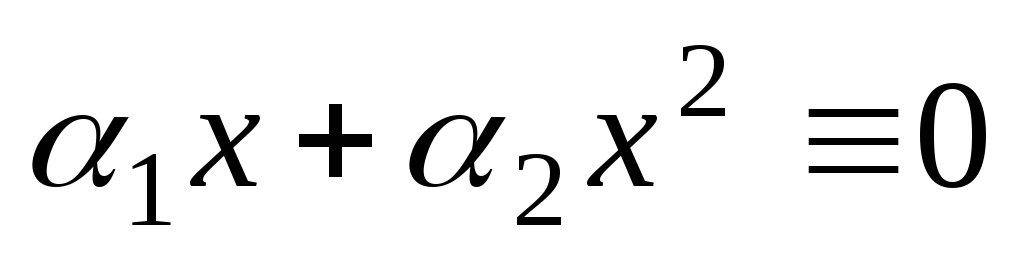 mogoče le, če in
mogoče le, če in 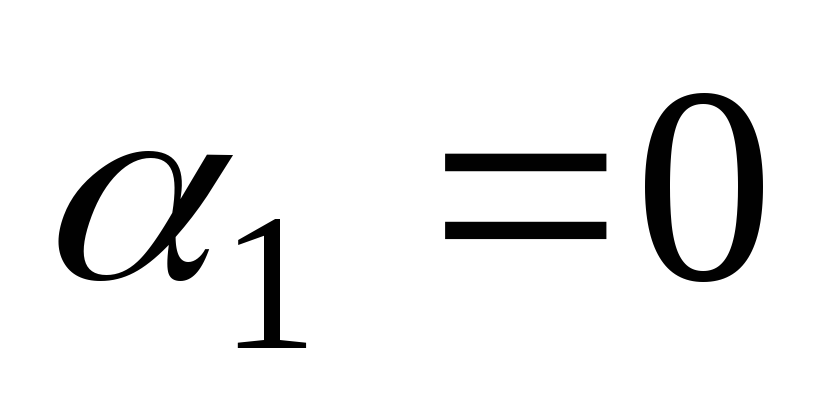 , in
, in 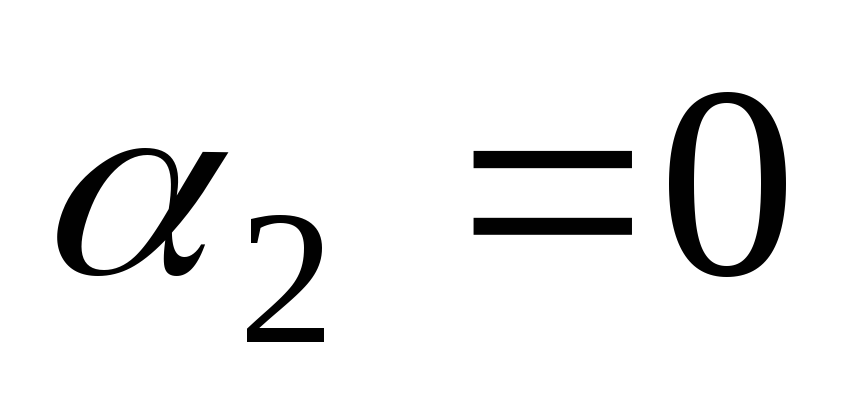 .
.
Konstrukcija splošne rešitve linearne homogenosti
enačbe
Da bi našli splošno rešitev enačbe (2), morate najti dve njeni linearno neodvisni rešitvi 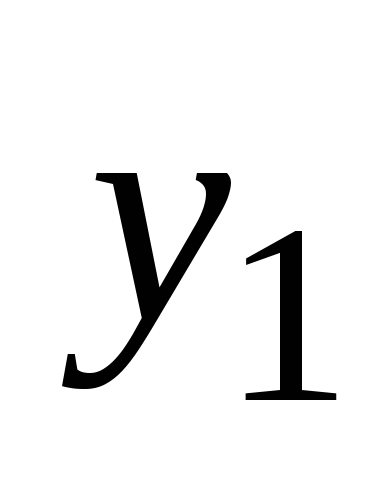 in
in 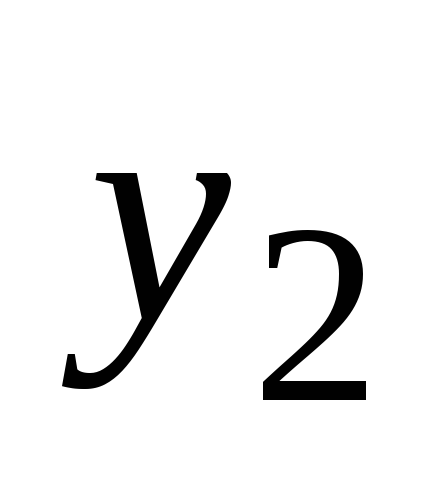 . Linearna kombinacija teh rešitev
. Linearna kombinacija teh rešitev 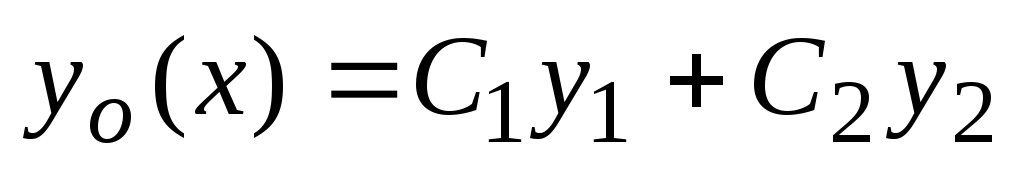 , kje
, kje 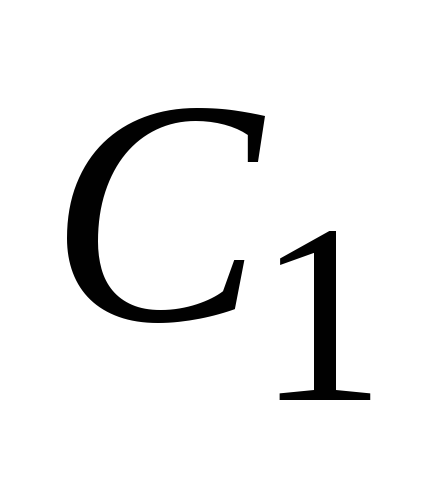 in
in 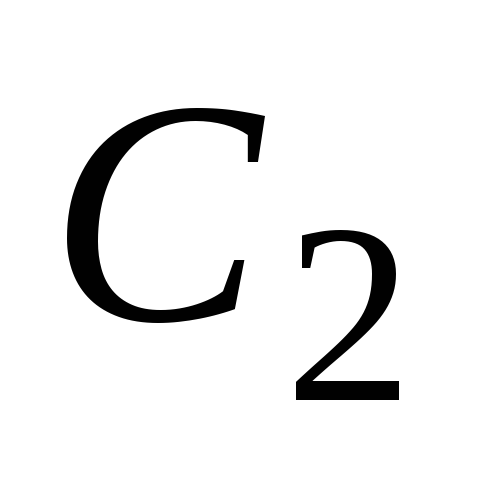 so poljubne konstante in bodo dale splošno rešitev linearne homogene enačbe.
so poljubne konstante in bodo dale splošno rešitev linearne homogene enačbe.
Linearno neodvisne rešitve enačbe (2) bomo iskali v obliki
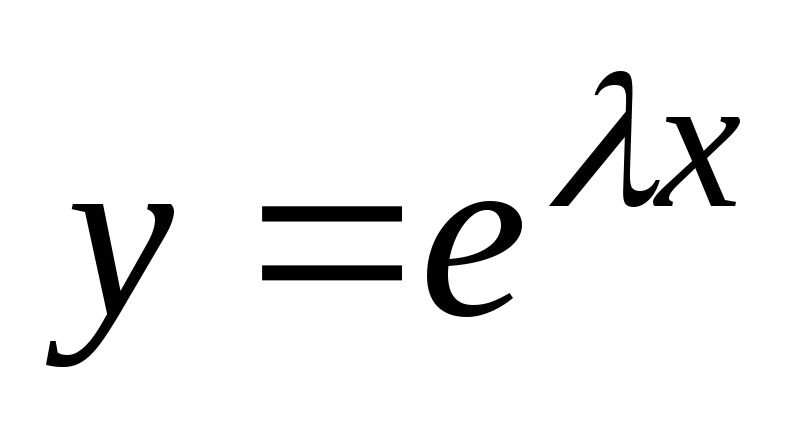 ,
(5)
,
(5)
kje  - nekaj številk. Potem
- nekaj številk. Potem 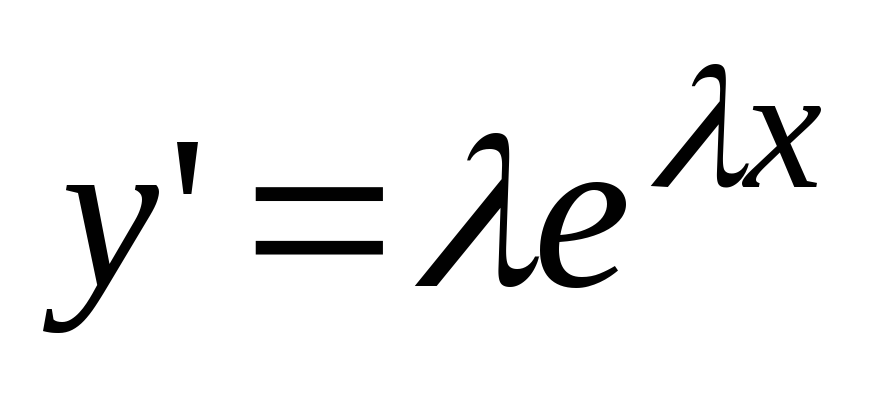 ,
,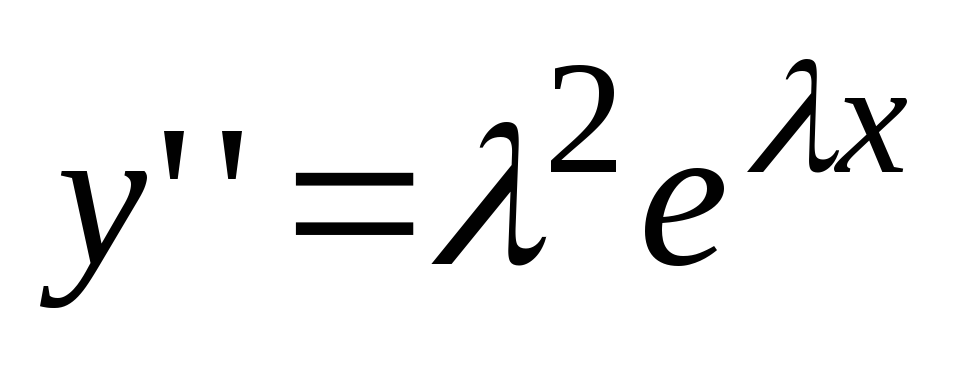 . Zamenjajmo te izraze v enačbo (2):
. Zamenjajmo te izraze v enačbo (2):
oz 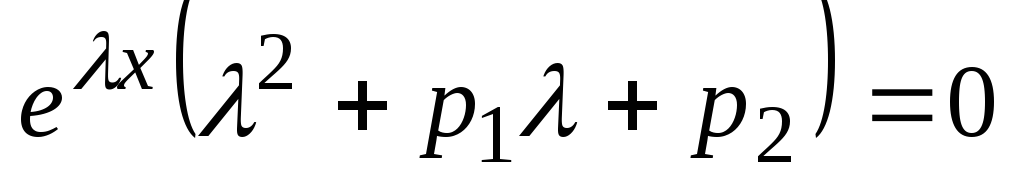 .
.
Ker 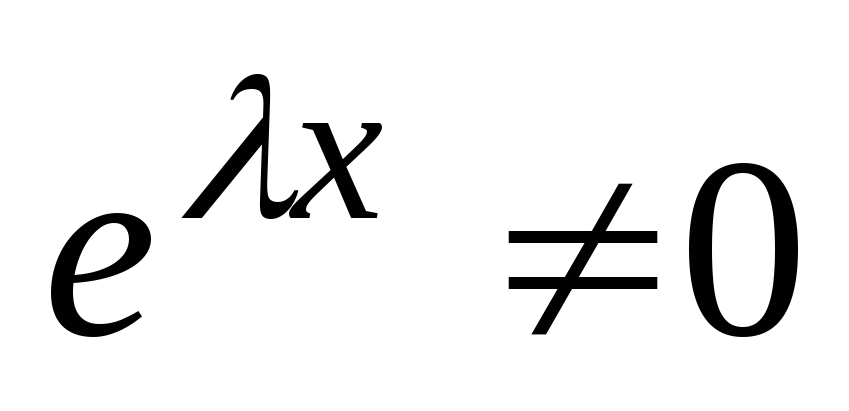 , potem
, potem 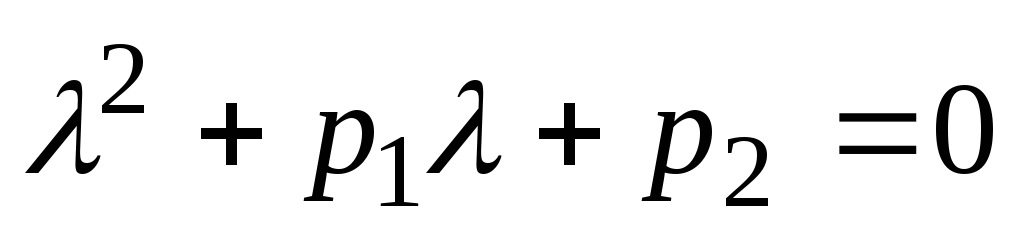 . Torej funkcija
. Torej funkcija 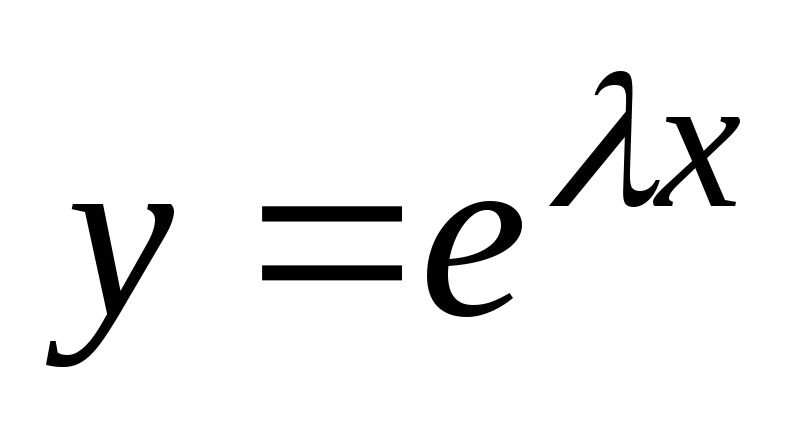 bo rešitev enačbe (2), če
bo rešitev enačbe (2), če  bo zadostil enačbi
bo zadostil enačbi
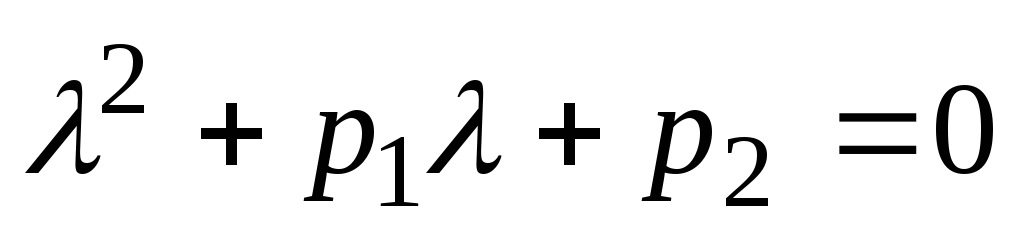 .
(6)
.
(6)
Enačba (6) se imenuje karakteristična enačba za enačbo (2). Ta enačba je algebraična kvadratna enačba.
Pustiti 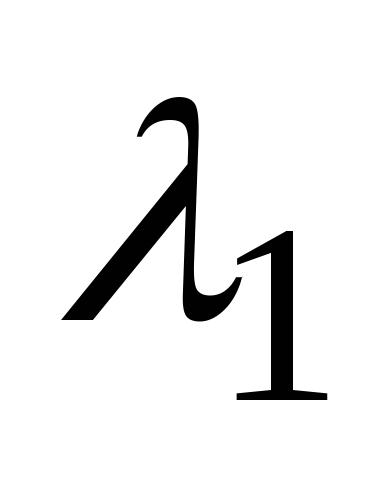 in
in ![]() so koreni te enačbe. Lahko so resnični in različni, kompleksni ali resnični in enakopravni. Razmislimo o teh primerih.
so koreni te enačbe. Lahko so resnični in različni, kompleksni ali resnični in enakopravni. Razmislimo o teh primerih.
 Pustite korenine
Pustite korenine 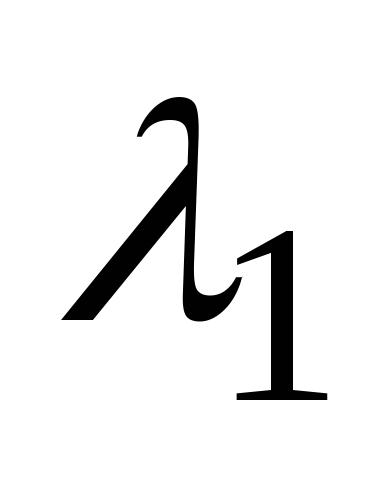 in
in ![]() karakteristične enačbe so realne in različne. Potem bodo rešitve enačbe (2) funkcije
karakteristične enačbe so realne in različne. Potem bodo rešitve enačbe (2) funkcije 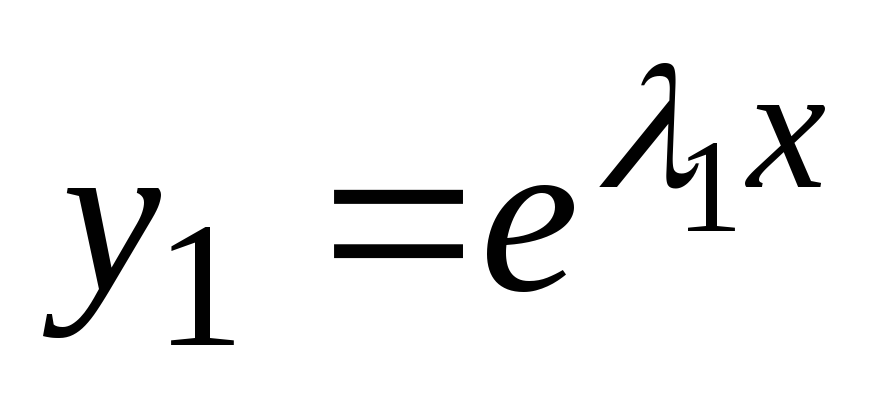 in
in 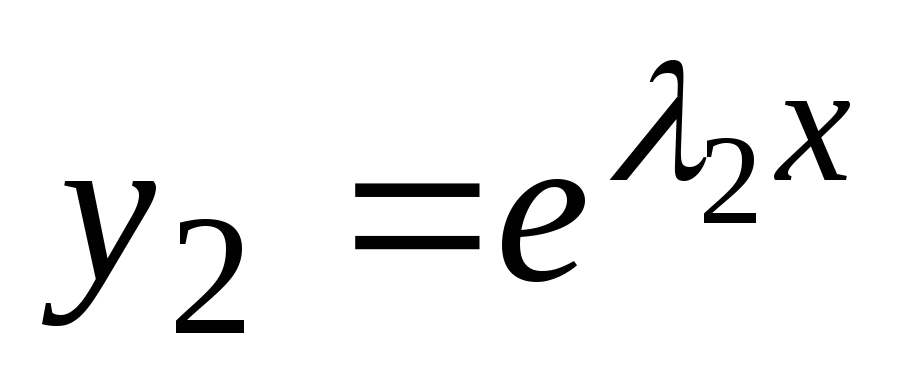 . Te rešitve so linearno neodvisne, saj je enakost
. Te rešitve so linearno neodvisne, saj je enakost 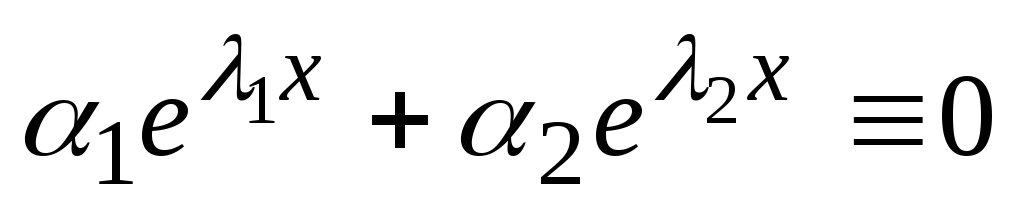 mogoče izvajati le, ko
mogoče izvajati le, ko 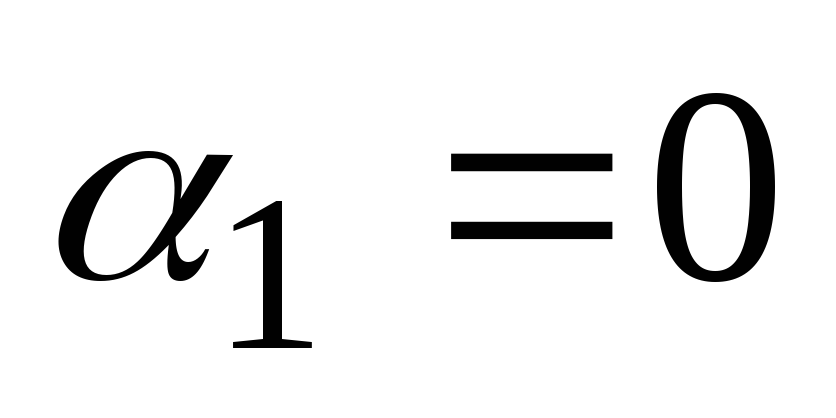 , in
, in 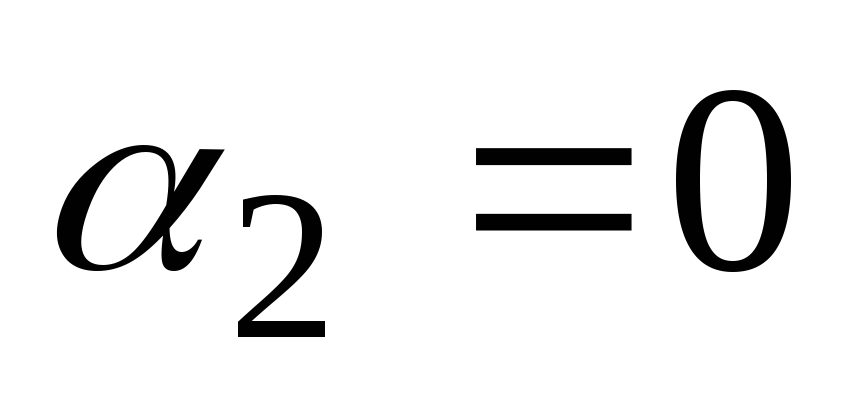 . Zato ima splošna rešitev enačbe (2) obliko
. Zato ima splošna rešitev enačbe (2) obliko
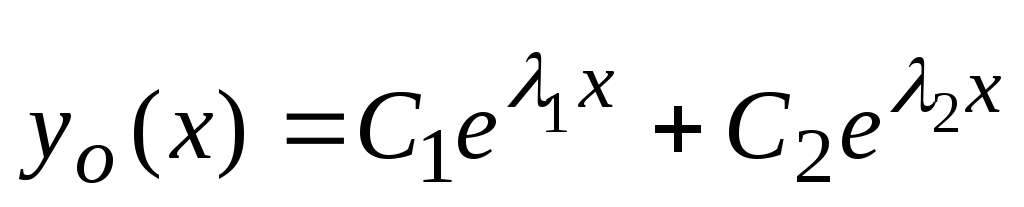 ,
,
kje 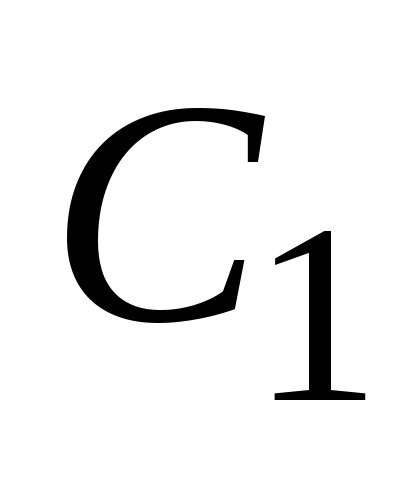 in
in  so poljubne konstante.
so poljubne konstante.
Primer 3
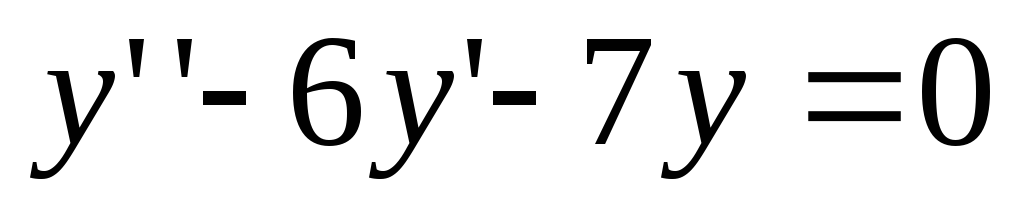 .
.
Rešitev
. Značilna enačba za ta diferencial bo 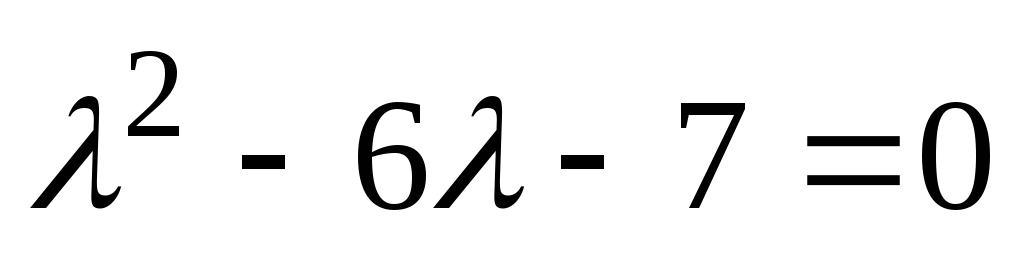 . Če rešimo to kvadratno enačbo, najdemo njene korenine
. Če rešimo to kvadratno enačbo, najdemo njene korenine 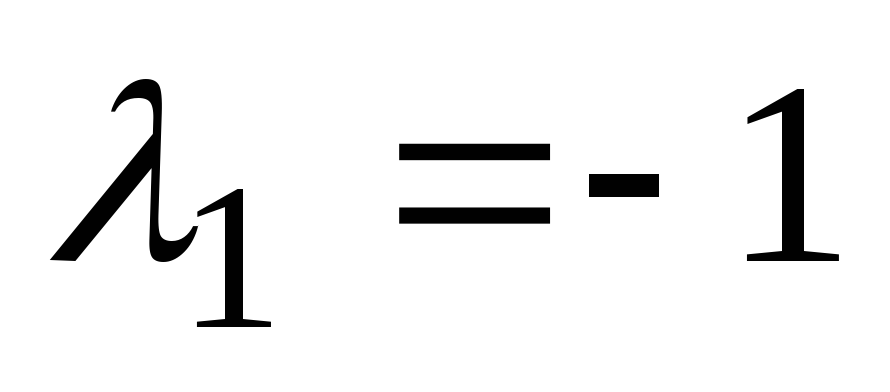 in
in 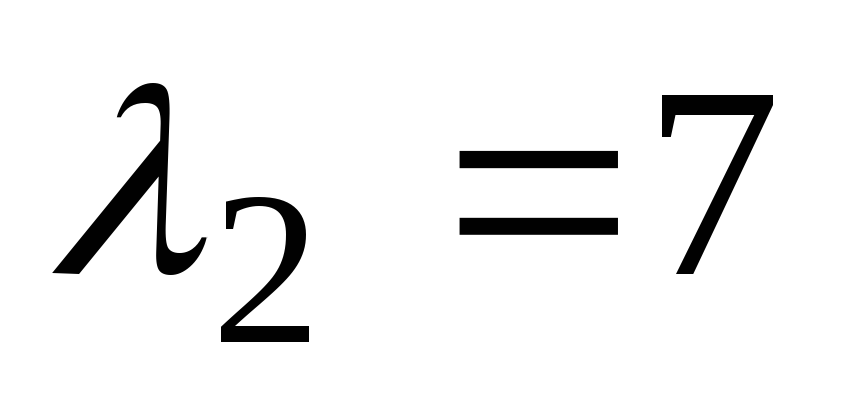 . Funkcije
. Funkcije 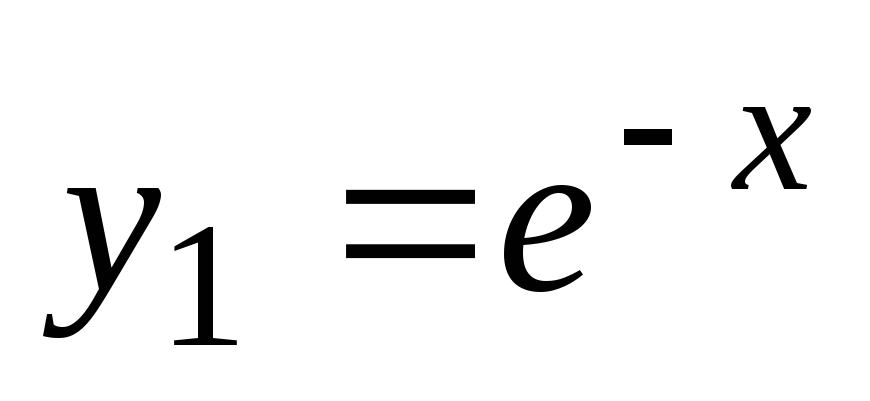 in
in 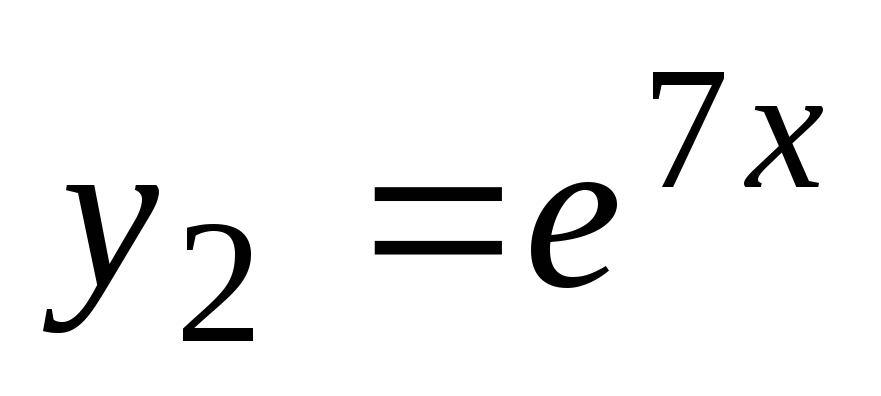 so rešitve diferencialne enačbe. Splošna rešitev te enačbe ima obliko
so rešitve diferencialne enačbe. Splošna rešitev te enačbe ima obliko 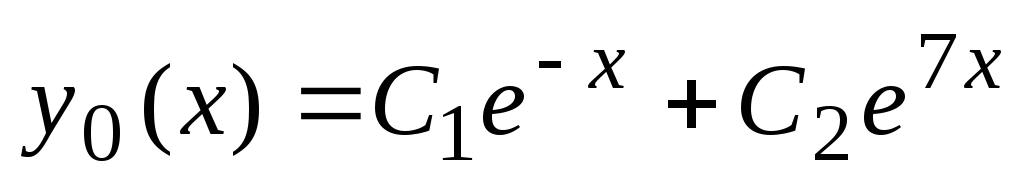 .
.
 kompleksno število
kompleksno število  se imenuje izraz oblike
se imenuje izraz oblike 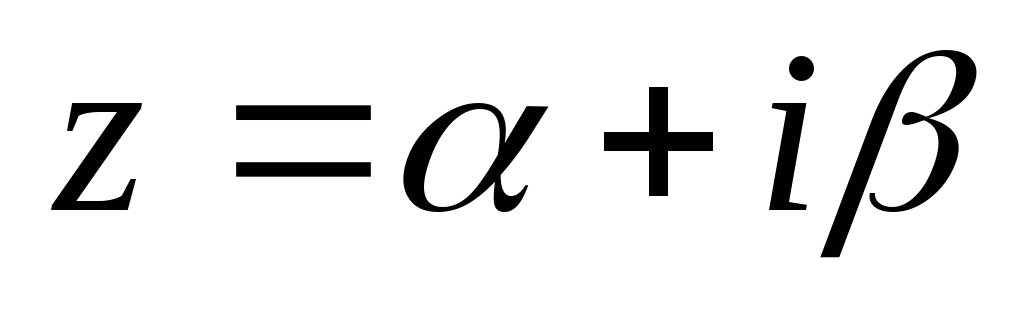 , kje
, kje  in
in  so realna števila in
so realna števila in 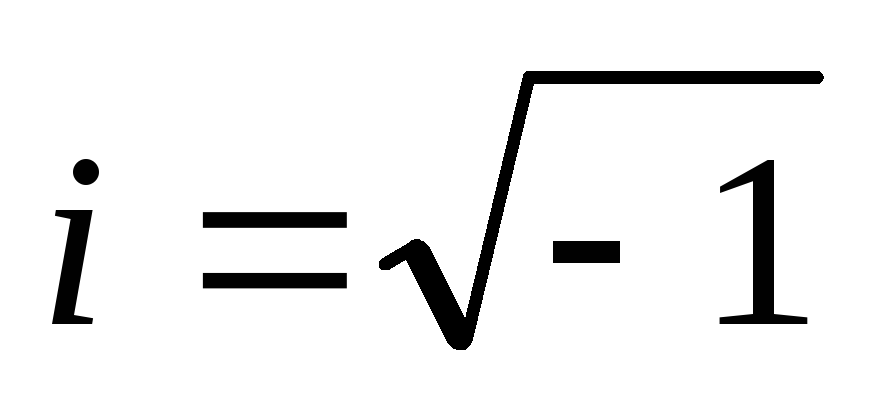 se imenuje imaginarna enota. Če
se imenuje imaginarna enota. Če 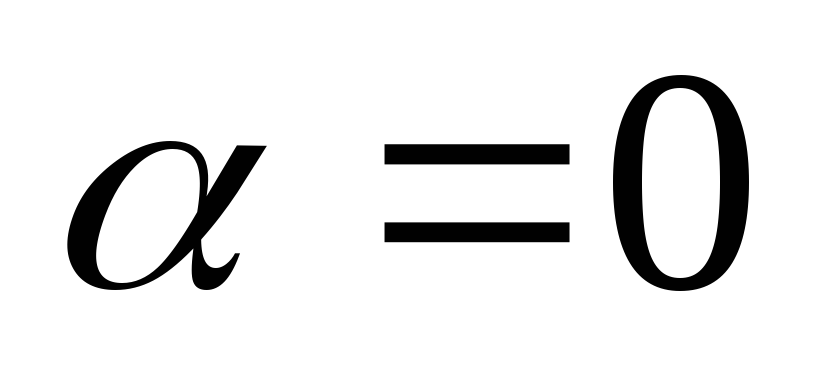 , nato številko
, nato številko 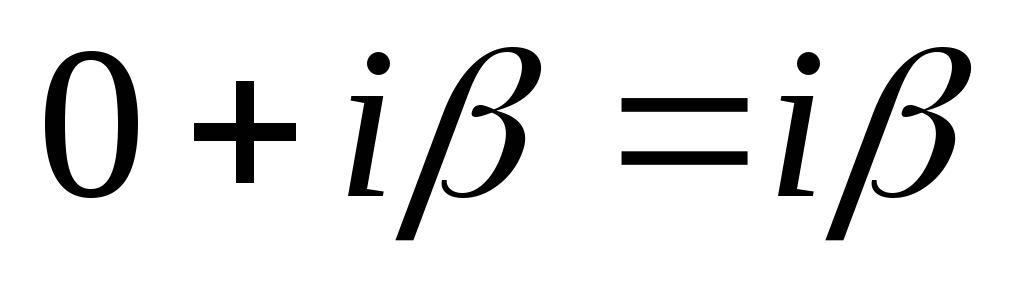 se imenuje čisto imaginaren. če
se imenuje čisto imaginaren. če 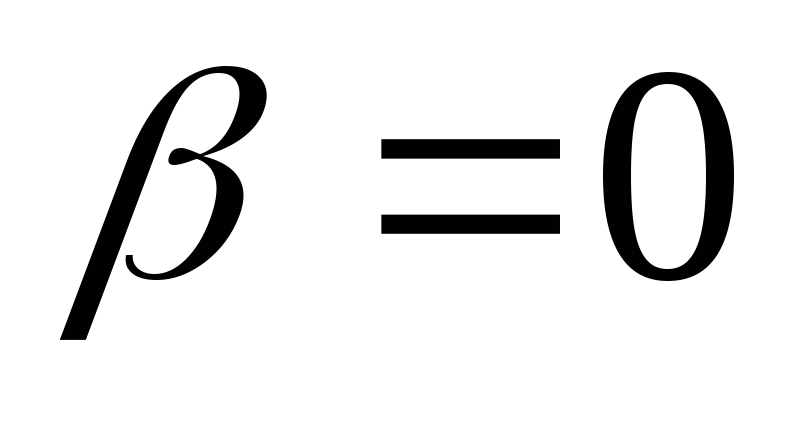 , nato številko
, nato številko 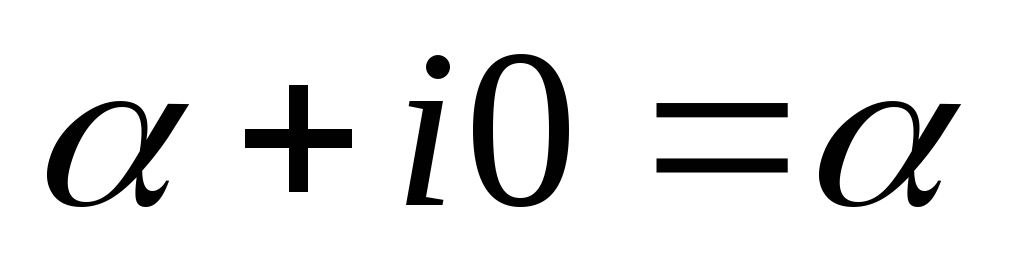 se identificira z realnim številom
se identificira z realnim številom  .
.
številka  se imenuje realni del kompleksnega števila in
se imenuje realni del kompleksnega števila in  - imaginarni del. Če se dve kompleksni števili med seboj razlikujeta samo v predznaku imaginarnega dela, se imenujeta konjugirani:
- imaginarni del. Če se dve kompleksni števili med seboj razlikujeta samo v predznaku imaginarnega dela, se imenujeta konjugirani: 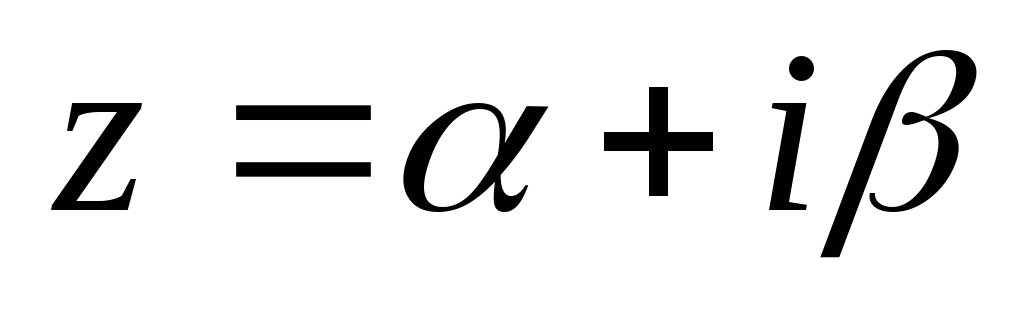 ,
,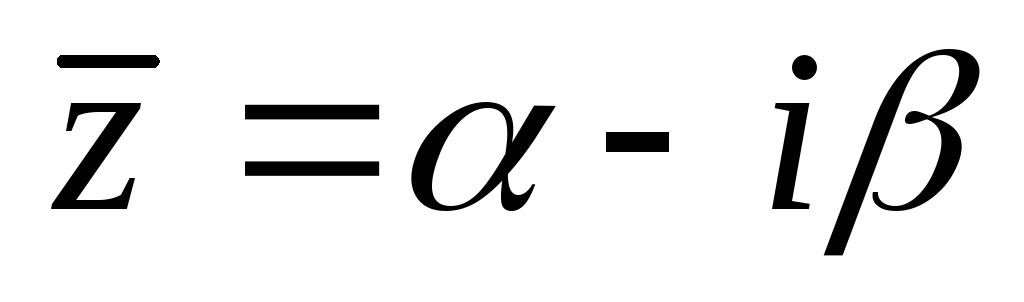 .
.
Primer 4
. Rešite kvadratno enačbo 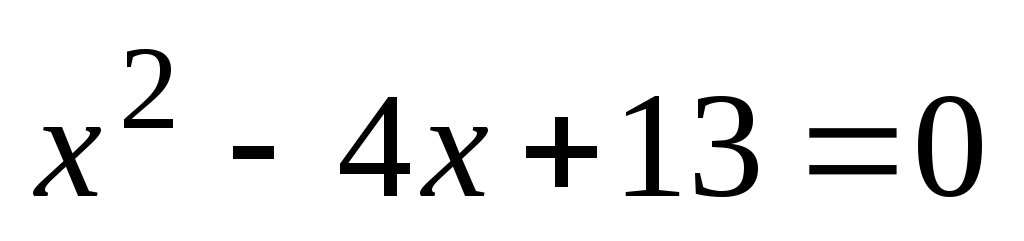 .
.
Rešitev
. Diskriminant enačbe 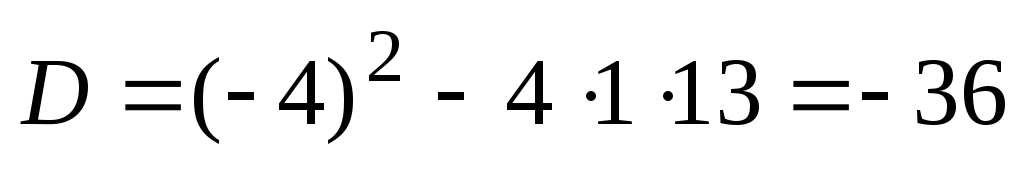 . Potem. prav tako
. Potem. prav tako 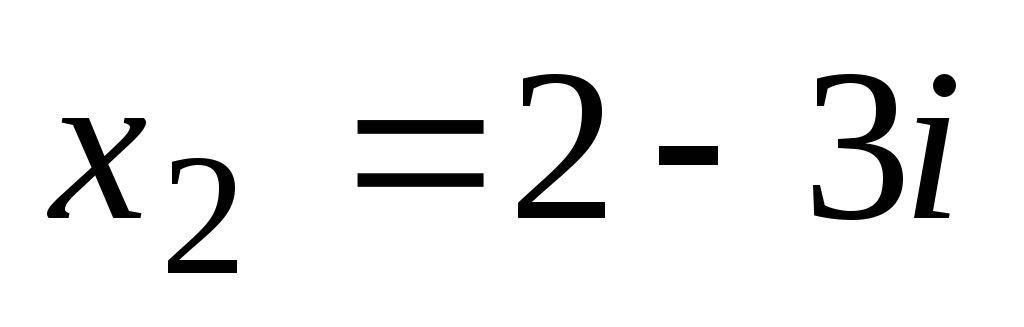 . Tako ima ta kvadratna enačba konjugirane kompleksne korenine.
. Tako ima ta kvadratna enačba konjugirane kompleksne korenine.
Naj bodo koreni značilne enačbe kompleksni, tj. 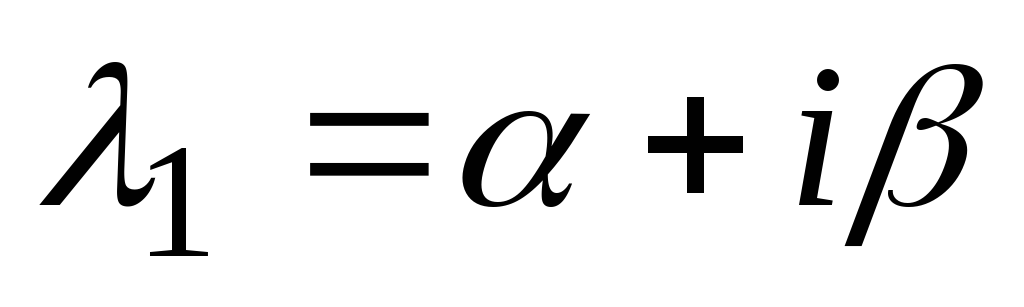 ,
,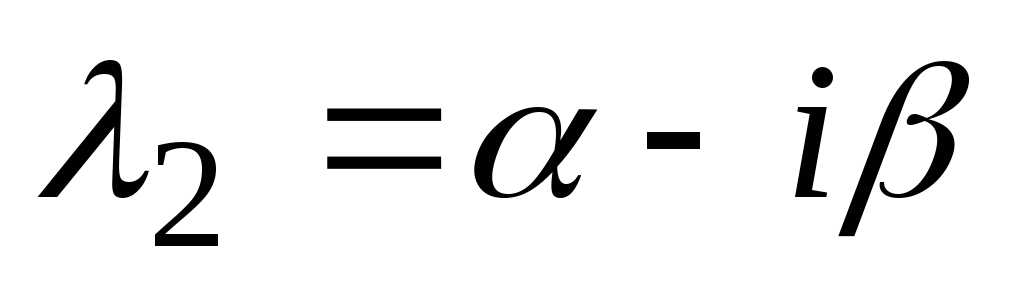 , kje
, kje 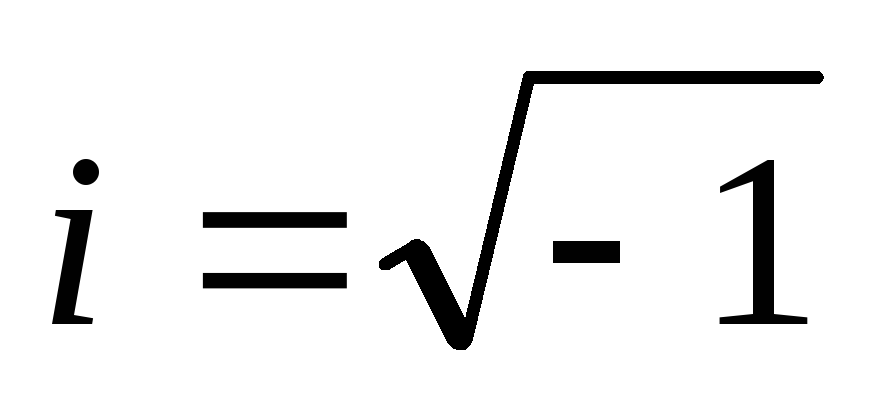 . Rešitve enačbe (2) lahko zapišemo kot
. Rešitve enačbe (2) lahko zapišemo kot 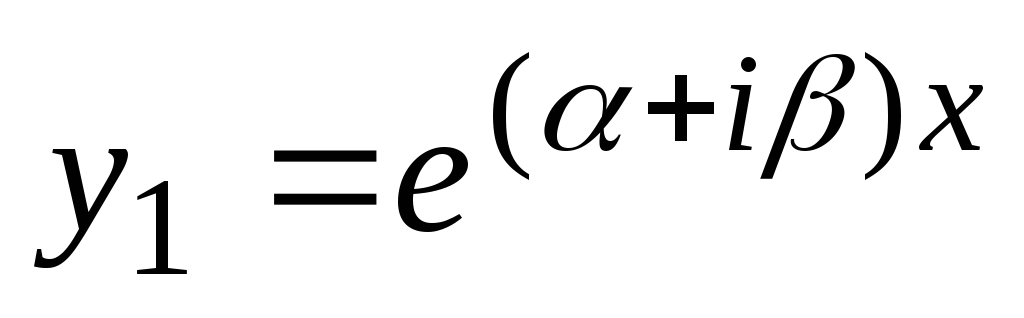 ,
,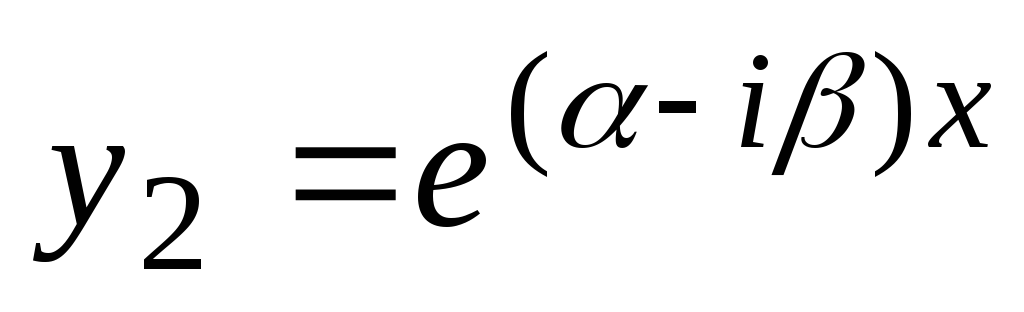 oz
oz 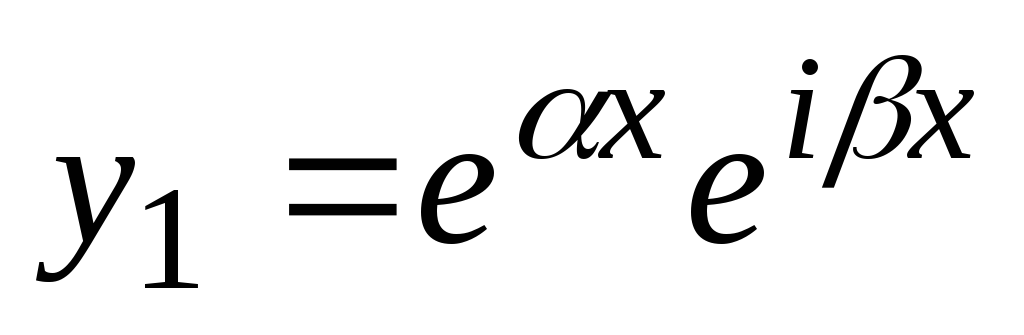 ,
,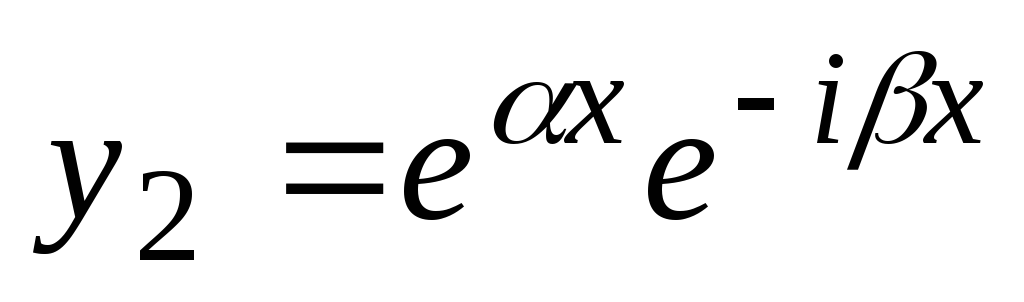 . Po Eulerjevih formulah
. Po Eulerjevih formulah
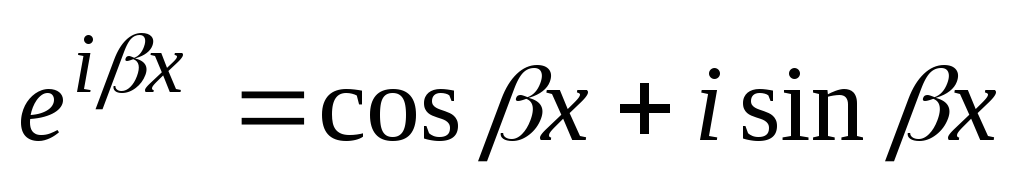 ,
,
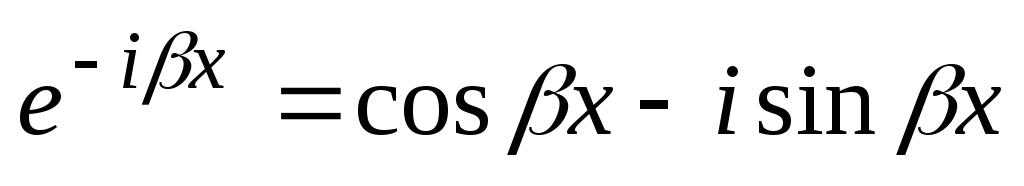 .
.
Potem,. Kot je znano, če je kompleksna funkcija rešitev linearne homogene enačbe, potem so rešitve te enačbe tako realni kot imaginarni deli te funkcije. Tako bodo rešitve enačbe (2) funkcije 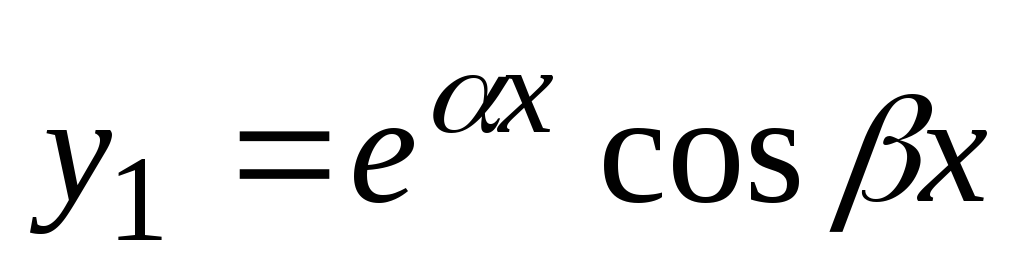 in
in 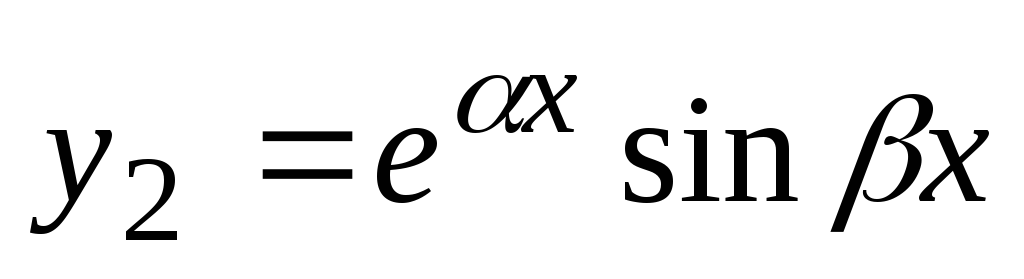 . Od enakosti
. Od enakosti
se lahko izvede le, če 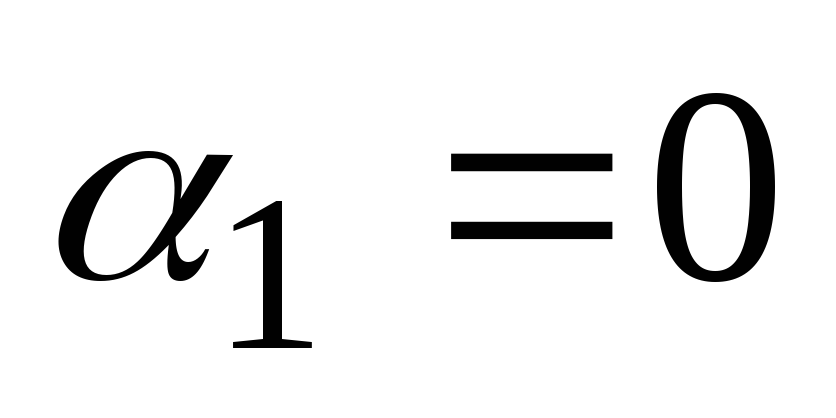 in
in 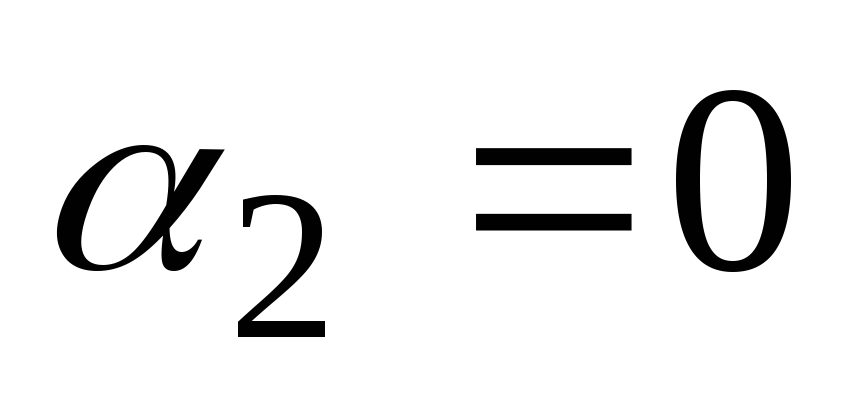 , potem so te rešitve linearno neodvisne. Zato ima splošna rešitev enačbe (2) obliko
, potem so te rešitve linearno neodvisne. Zato ima splošna rešitev enačbe (2) obliko
kje 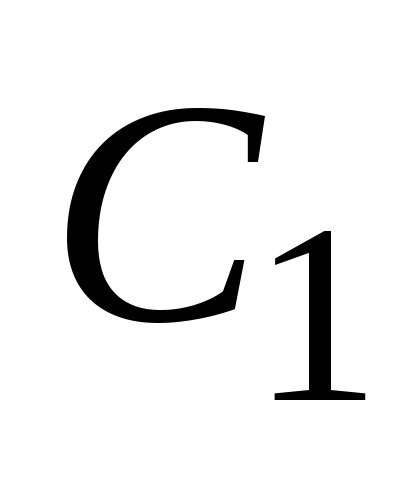 in
in  so poljubne konstante.
so poljubne konstante.
Primer 5
. Poiščite splošno rešitev diferencialne enačbe 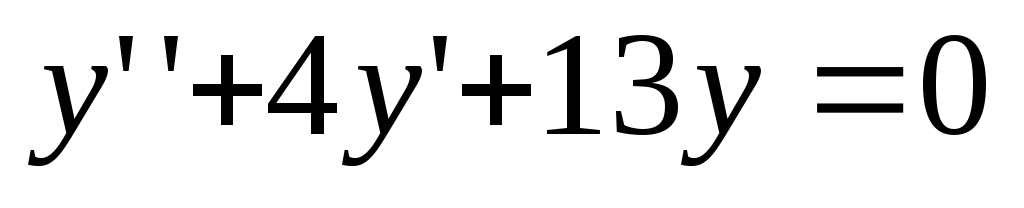 .
.
Rešitev
. Enačba 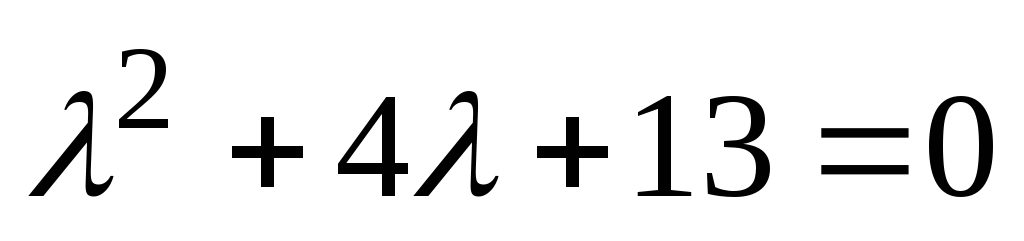 je značilen za dani diferencial. Rešimo jo in dobimo kompleksne korene
je značilen za dani diferencial. Rešimo jo in dobimo kompleksne korene 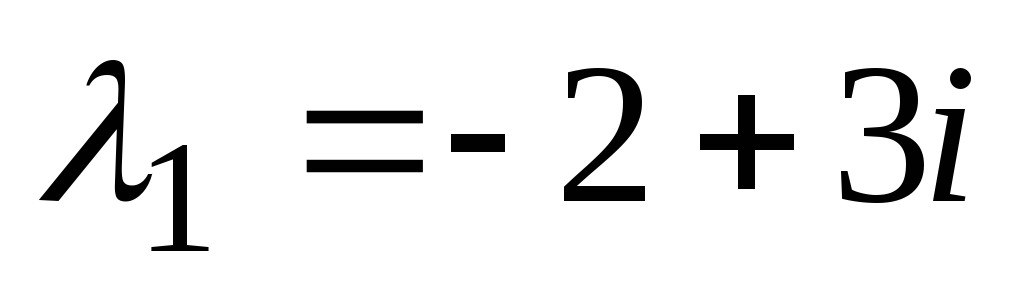 ,
,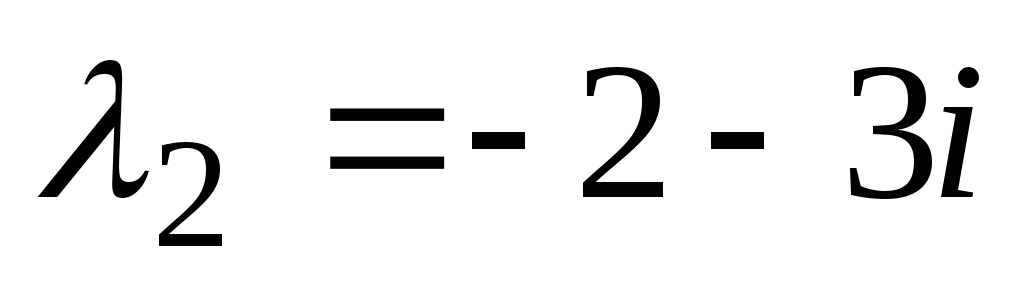 . Funkcije
. Funkcije 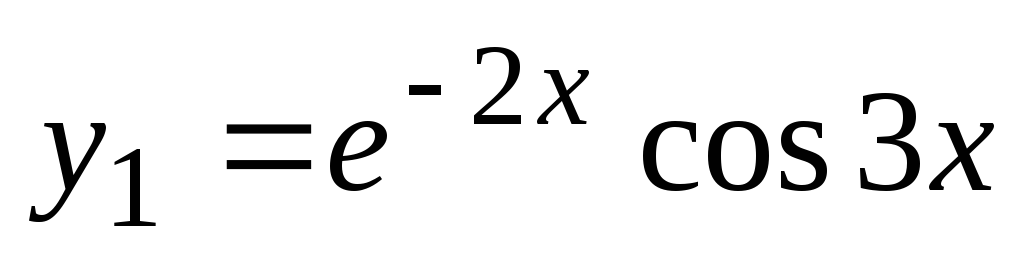 in
in 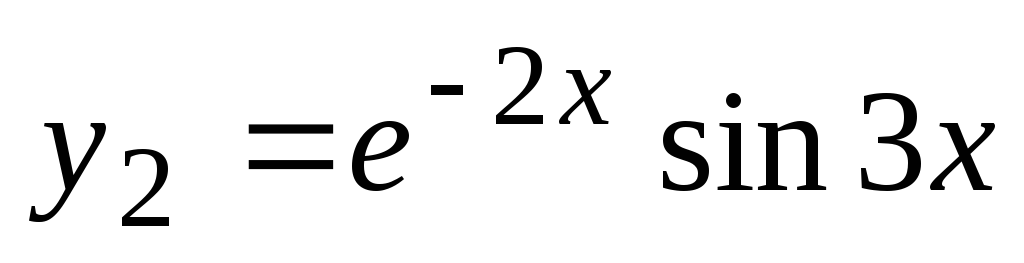 so linearno neodvisne rešitve diferencialne enačbe. Splošna rešitev te enačbe ima obliko.
so linearno neodvisne rešitve diferencialne enačbe. Splošna rešitev te enačbe ima obliko.
 Naj bodo korenine karakteristične enačbe realne in enake, tj.
Naj bodo korenine karakteristične enačbe realne in enake, tj. 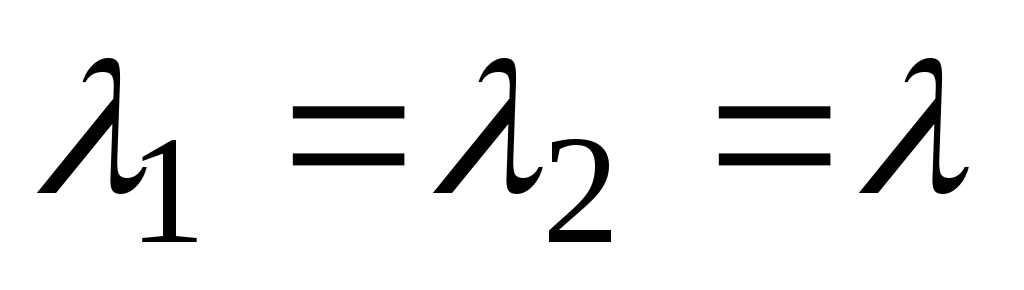 . Potem so rešitve enačbe (2) funkcije
. Potem so rešitve enačbe (2) funkcije 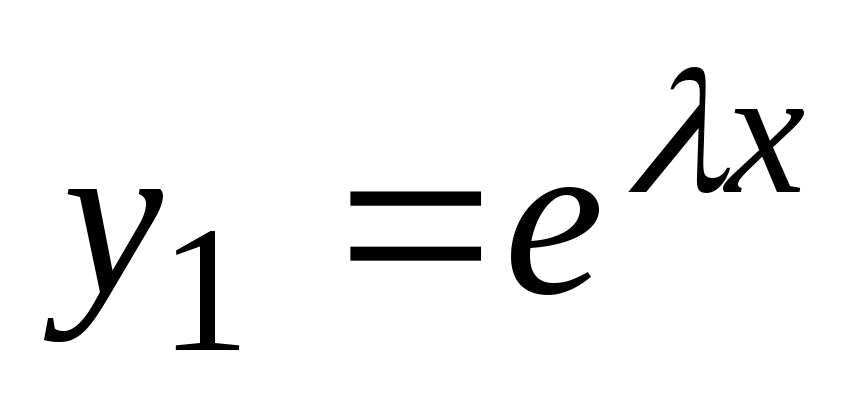 in
in 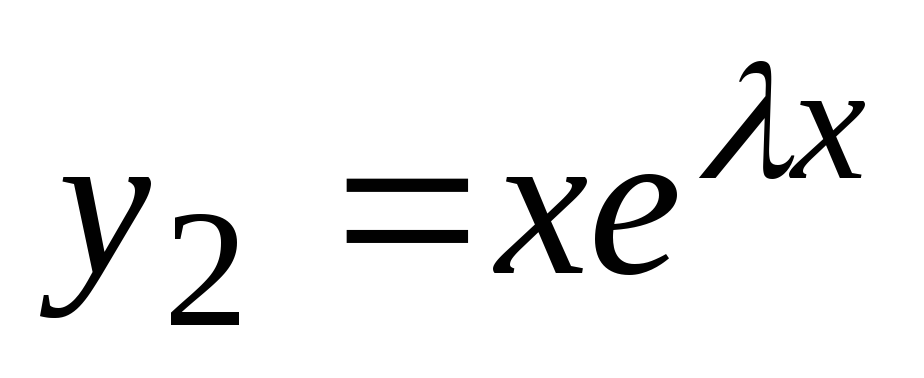 . Te rešitve so linearno neodvisne, saj je lahko izraz identično enak nič le, če
. Te rešitve so linearno neodvisne, saj je lahko izraz identično enak nič le, če 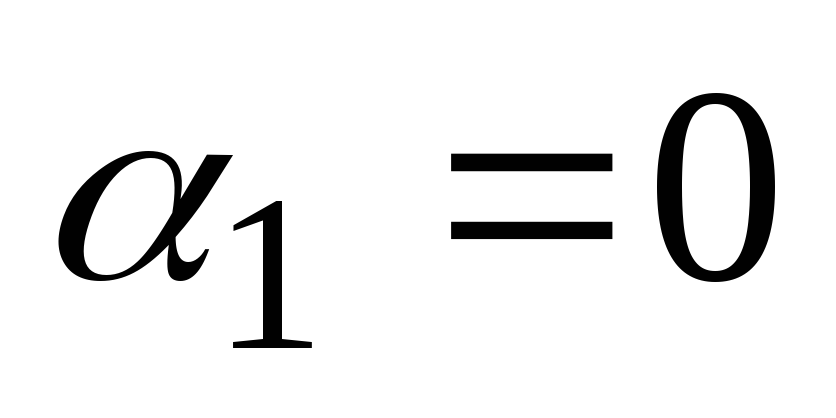 in
in 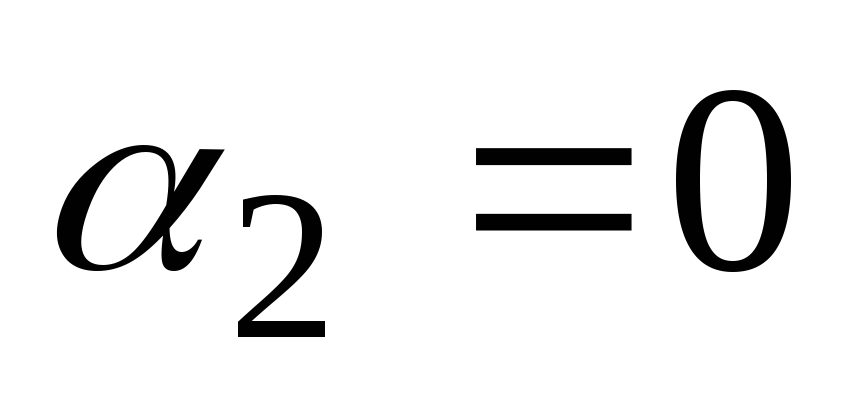 . Zato ima splošna rešitev enačbe (2) obliko
. Zato ima splošna rešitev enačbe (2) obliko 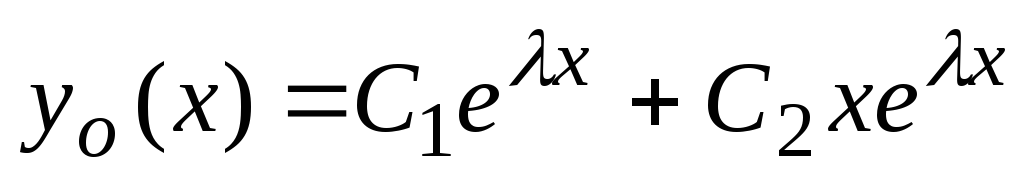 .
.
Primer 6
. Poiščite splošno rešitev diferencialne enačbe 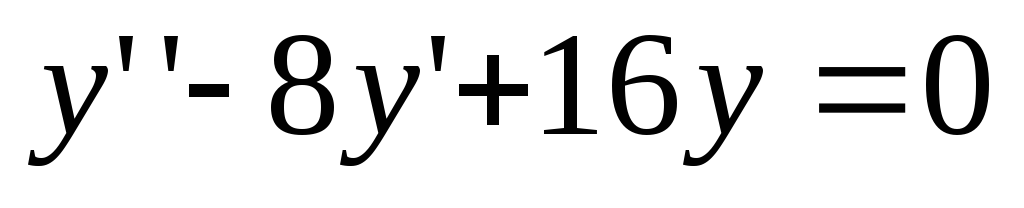 .
.
Rešitev
. Karakteristična enačba 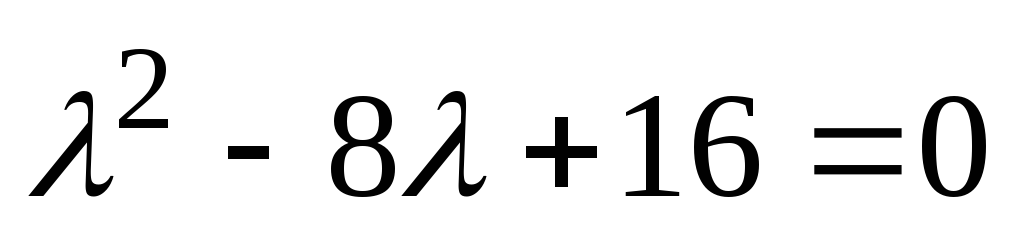 ima enake korenine
ima enake korenine 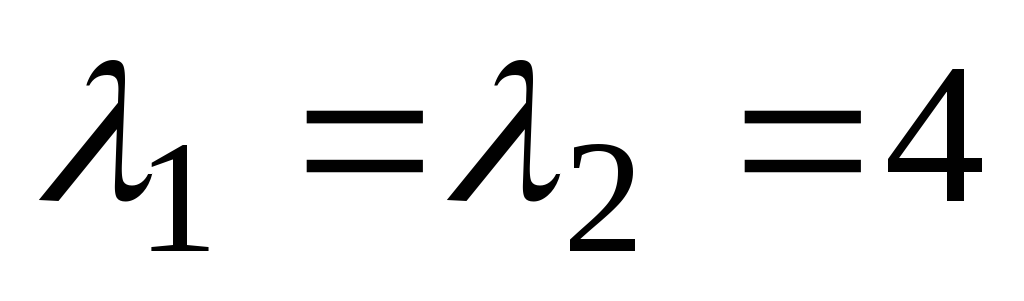 . V tem primeru so linearno neodvisne rešitve diferencialne enačbe funkcije
. V tem primeru so linearno neodvisne rešitve diferencialne enačbe funkcije 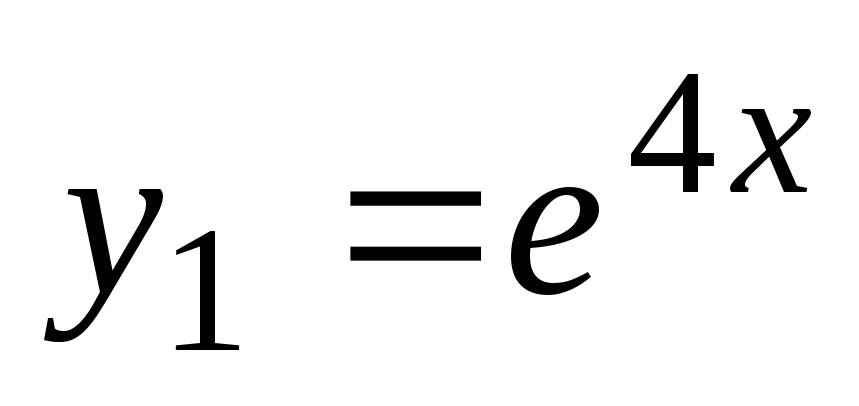 in
in 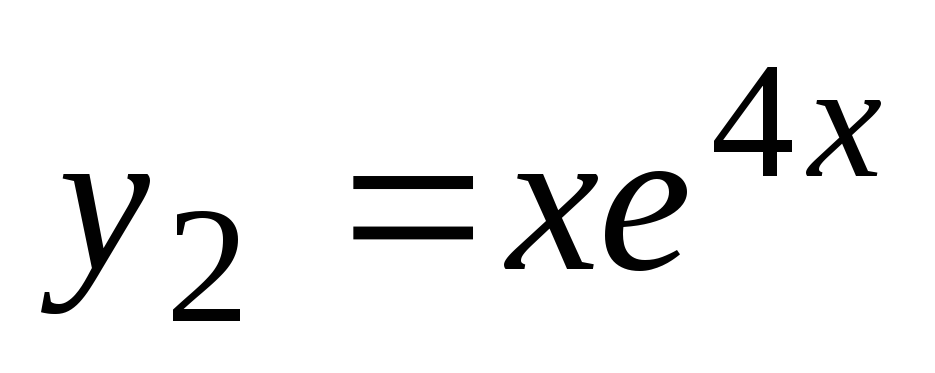 . Splošna rešitev ima obliko
. Splošna rešitev ima obliko 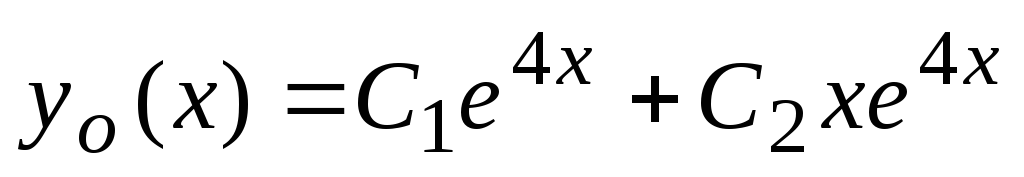 .
.
Nehomogene linearne diferencialne enačbe drugega reda s konstantnimi koeficienti
in posebna desna stran
Splošna rešitev linearne nehomogene enačbe (1) je enaka vsoti splošne rešitve 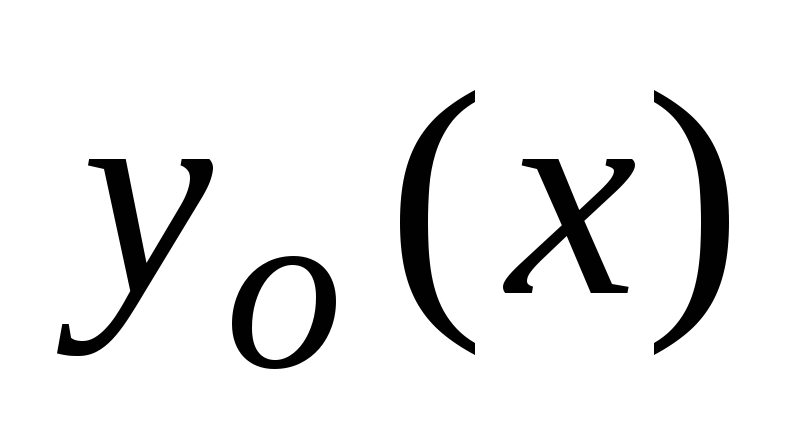 ustrezna homogena enačba in katera koli posebna rešitev
ustrezna homogena enačba in katera koli posebna rešitev 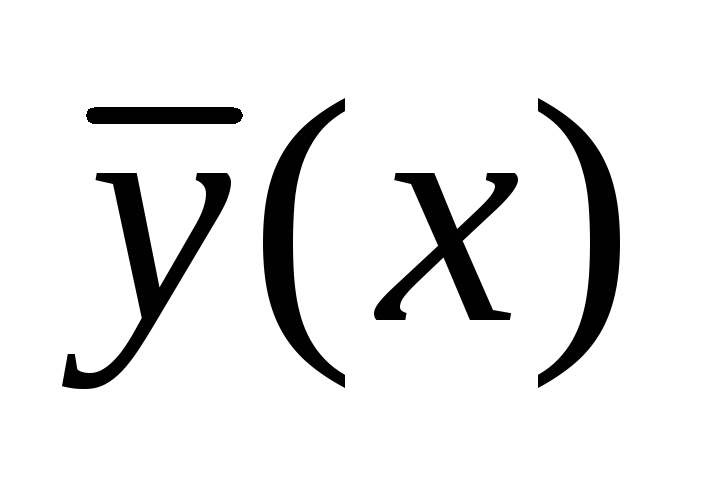 nehomogena enačba:
nehomogena enačba: 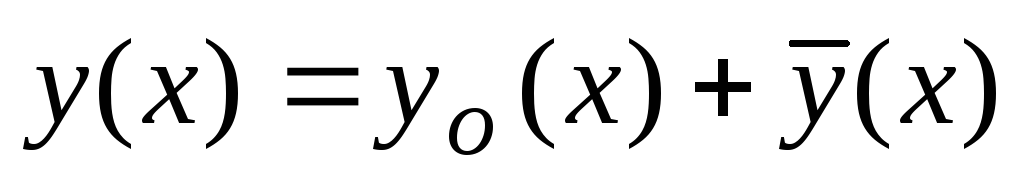 .
.
V nekaterih primerih lahko posamezno rešitev nehomogene enačbe preprosto najdemo z obliko desne strani 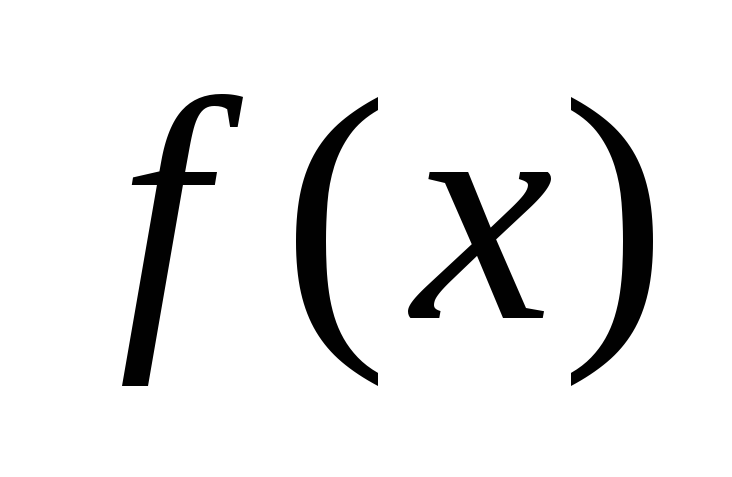 enačbe (1). Razmislimo o primerih, ko je to mogoče.
enačbe (1). Razmislimo o primerih, ko je to mogoče.
tiste. desna stran nehomogene enačbe je polinom stopnje m. Če 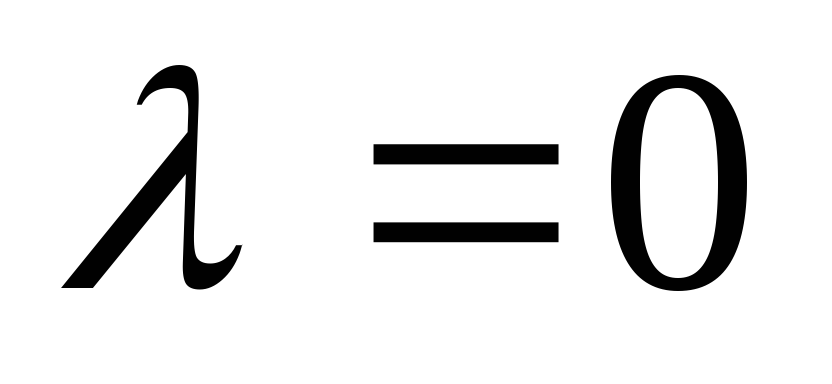 ni koren karakteristične enačbe, potem je treba določeno rešitev nehomogene enačbe iskati v obliki polinoma stopnje m, tj.
ni koren karakteristične enačbe, potem je treba določeno rešitev nehomogene enačbe iskati v obliki polinoma stopnje m, tj.
kvote ![]() se določijo v procesu iskanja določene rešitve.
se določijo v procesu iskanja določene rešitve.
če 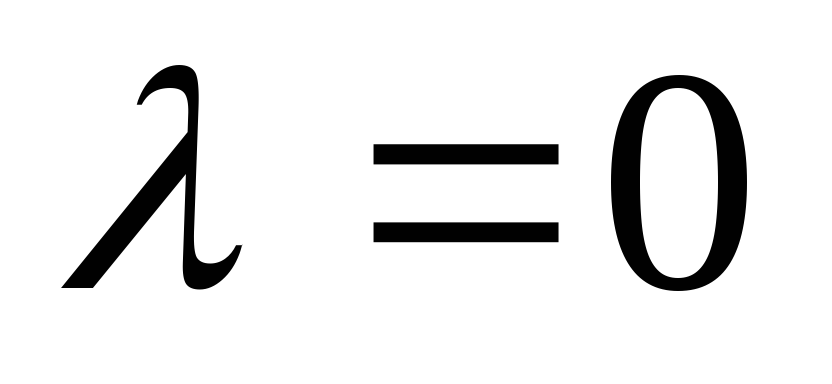 je koren karakteristične enačbe, potem je treba določeno rešitev nehomogene enačbe iskati v obliki
je koren karakteristične enačbe, potem je treba določeno rešitev nehomogene enačbe iskati v obliki
Primer 7
. Poiščite splošno rešitev diferencialne enačbe  .
.
Rešitev
. Ustrezna homogena enačba za to enačbo je 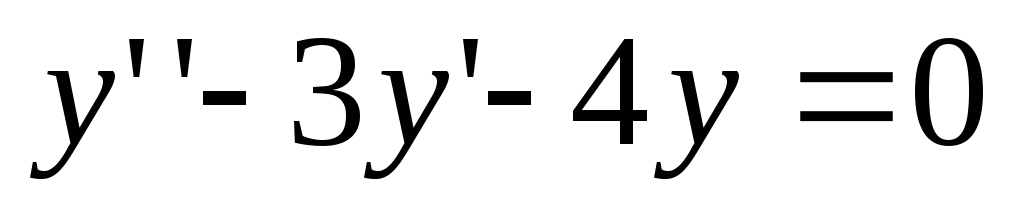 . Njegova značilna enačba
. Njegova značilna enačba 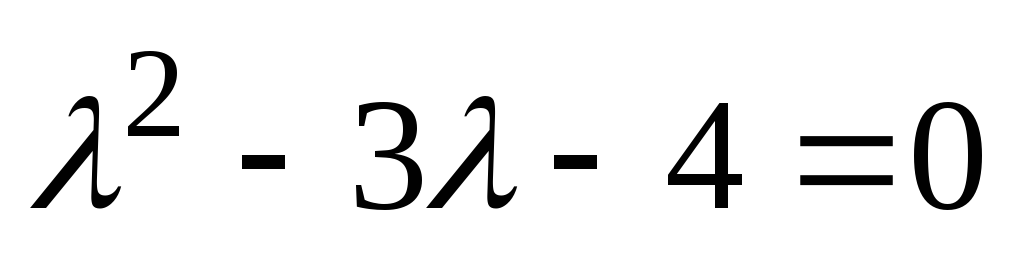 ima korenine
ima korenine 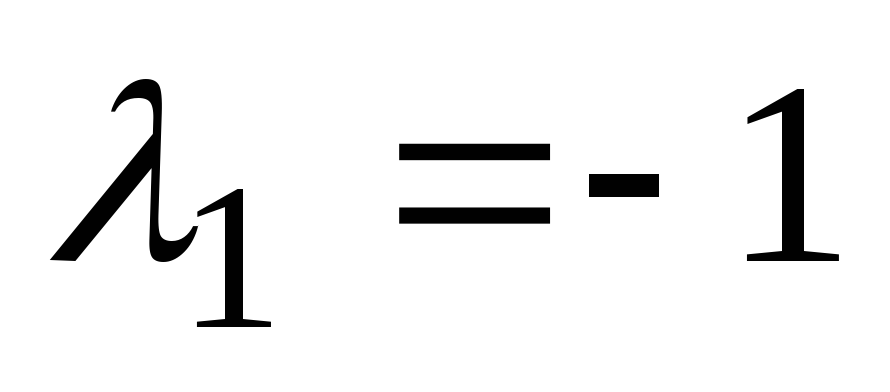 in
in 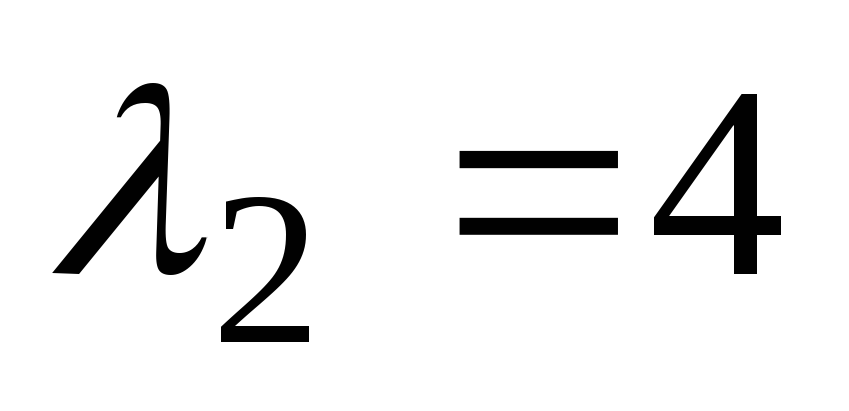 . Splošna rešitev homogene enačbe ima obliko
. Splošna rešitev homogene enačbe ima obliko 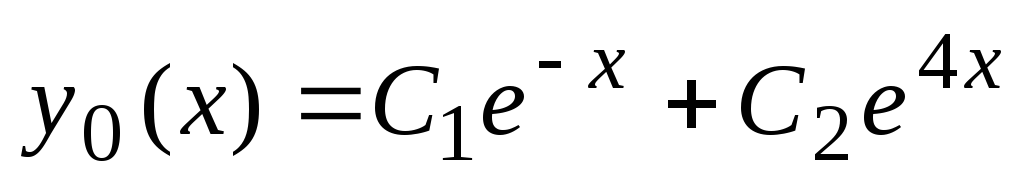 .
.
Ker 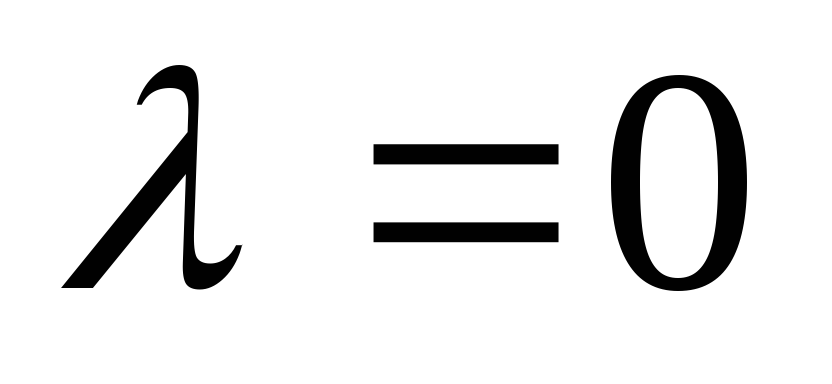 ni koren karakteristične enačbe, potem bomo partikularno rešitev nehomogene enačbe iskali v obliki funkcije
ni koren karakteristične enačbe, potem bomo partikularno rešitev nehomogene enačbe iskali v obliki funkcije 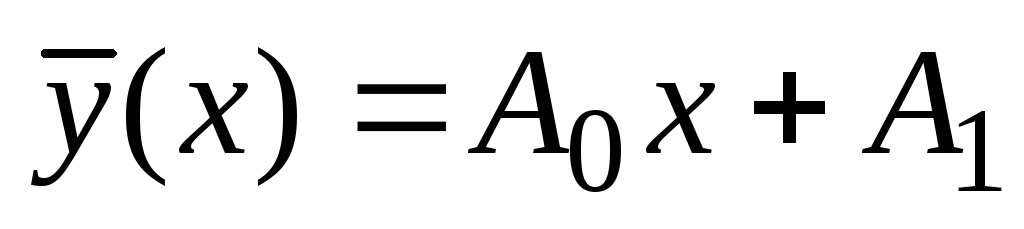 . Poiščite odvode te funkcije
. Poiščite odvode te funkcije 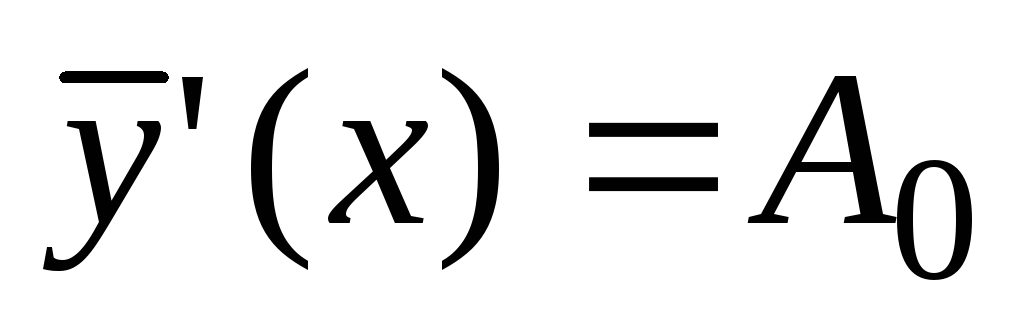 ,
,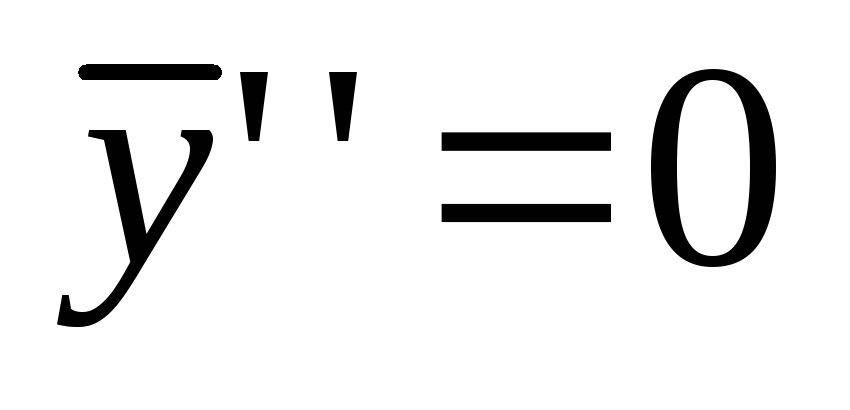 in jih nadomestite v to enačbo:
in jih nadomestite v to enačbo:
ali . Izenačite koeficiente pri 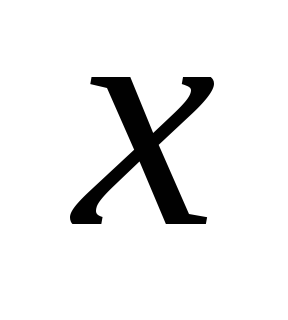 in brezplačni člani:
in brezplačni člani: 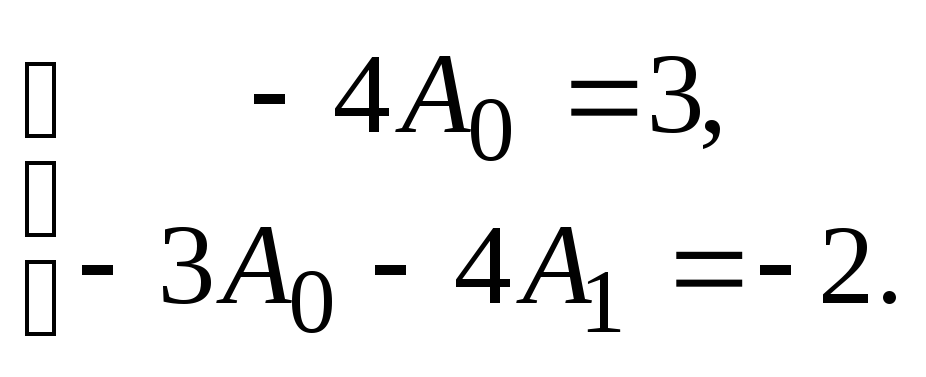 Če rešimo ta sistem, dobimo
Če rešimo ta sistem, dobimo 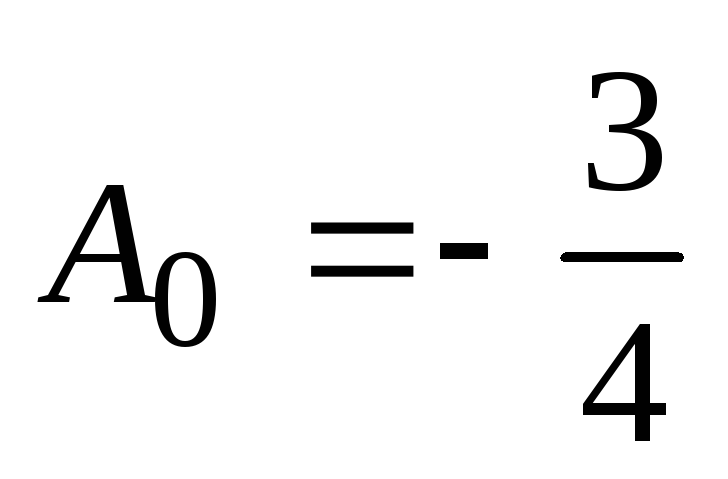 ,
,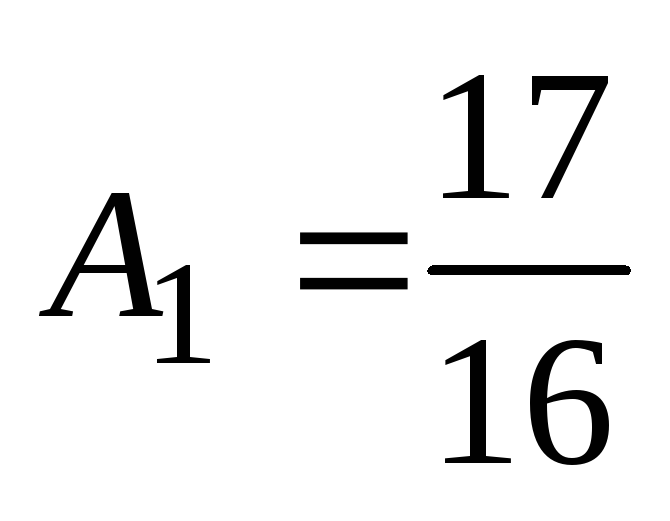 . Takrat ima določena rešitev nehomogene enačbe obliko
. Takrat ima določena rešitev nehomogene enačbe obliko ![]() , splošna rešitev te nehomogene enačbe pa bo vsota splošne rešitve ustrezne homogene enačbe in partikularne rešitve nehomogene:
, splošna rešitev te nehomogene enačbe pa bo vsota splošne rešitve ustrezne homogene enačbe in partikularne rešitve nehomogene: 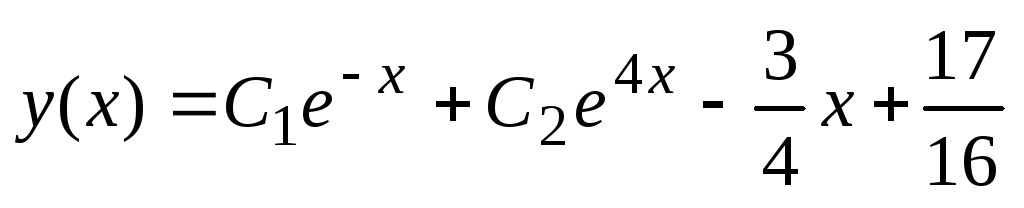 .
.
Naj ima nehomogena enačba obliko
Če 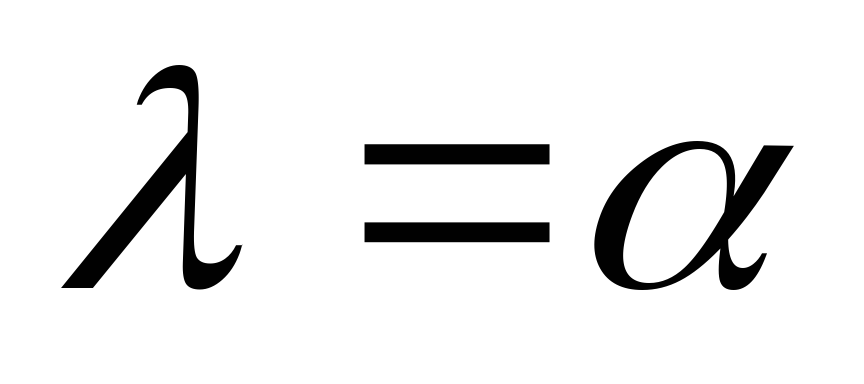 ni koren karakteristične enačbe, potem je treba partikularno rešitev nehomogene enačbe iskati v obliki. če
ni koren karakteristične enačbe, potem je treba partikularno rešitev nehomogene enačbe iskati v obliki. če 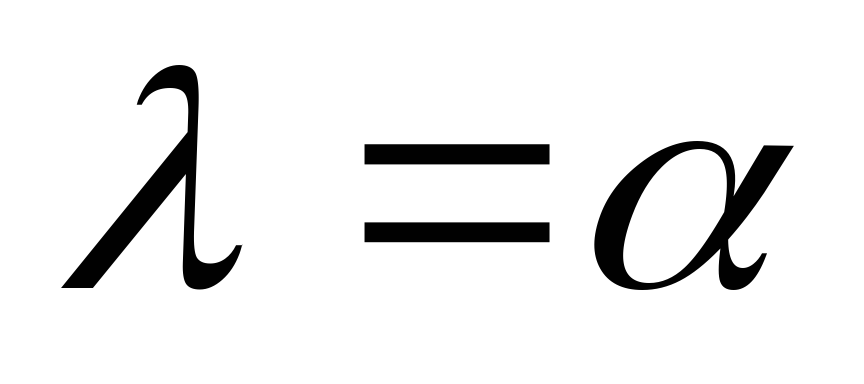 je koren enačbe karakteristične večkratnosti k
(k=1 oz k=2), potem bo imela v tem primeru partikularna rešitev nehomogene enačbe obliko .
je koren enačbe karakteristične večkratnosti k
(k=1 oz k=2), potem bo imela v tem primeru partikularna rešitev nehomogene enačbe obliko .
Primer 8
. Poiščite splošno rešitev diferencialne enačbe 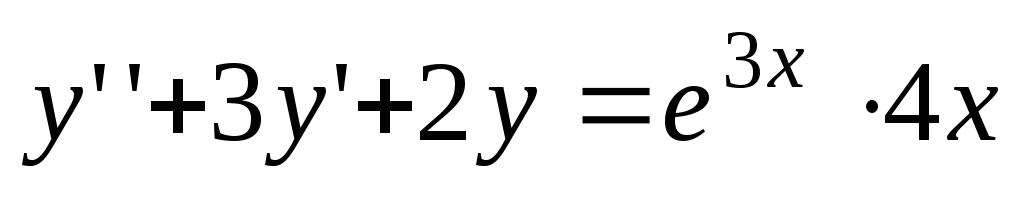 .
.
Rešitev
. Karakteristična enačba za pripadajočo homogeno enačbo ima obliko 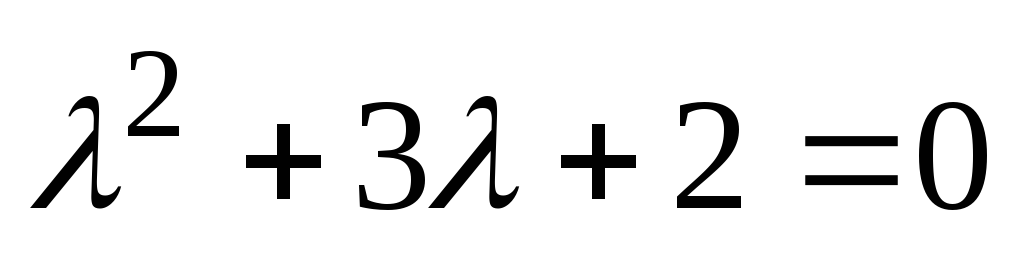 . svoje korenine
. svoje korenine 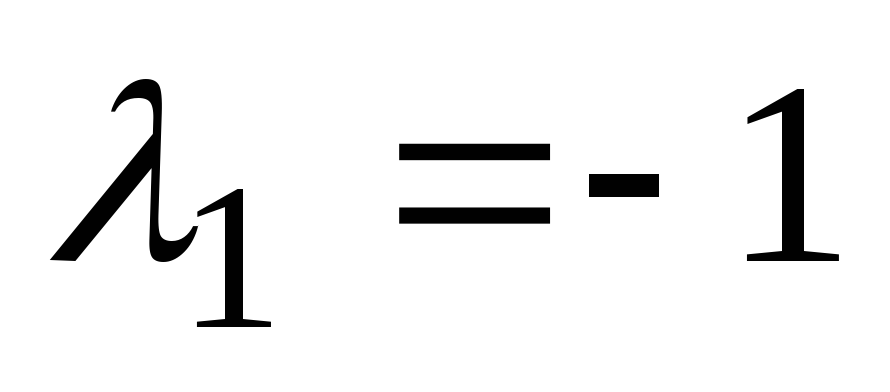 ,
,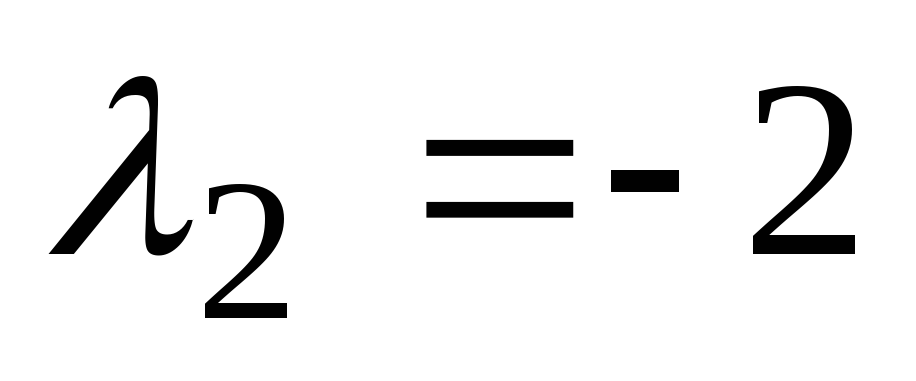 . V tem primeru je splošna rešitev ustrezne homogene enačbe zapisana kot
. V tem primeru je splošna rešitev ustrezne homogene enačbe zapisana kot 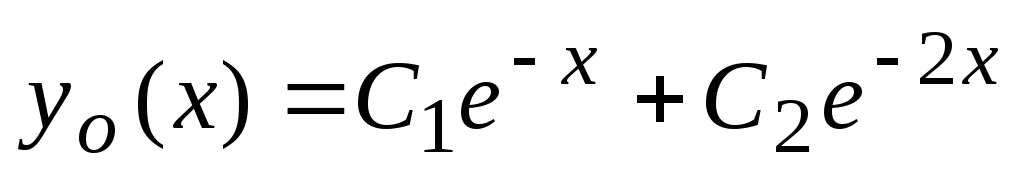 .
.
Ker število 3 ni koren karakteristične enačbe, je treba posebno rešitev nehomogene enačbe iskati v obliki 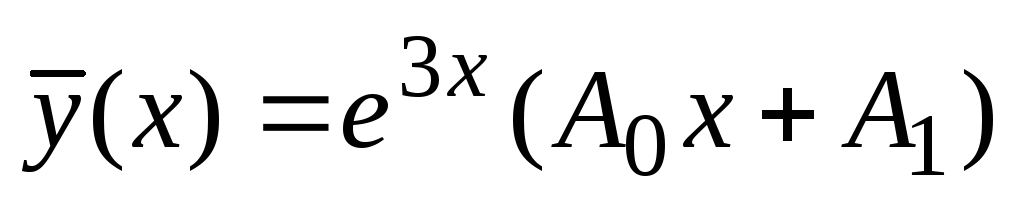 . Poiščimo izpeljanke prvega in drugega reda:,
. Poiščimo izpeljanke prvega in drugega reda:,
Zamenjajte v diferencialno enačbo: 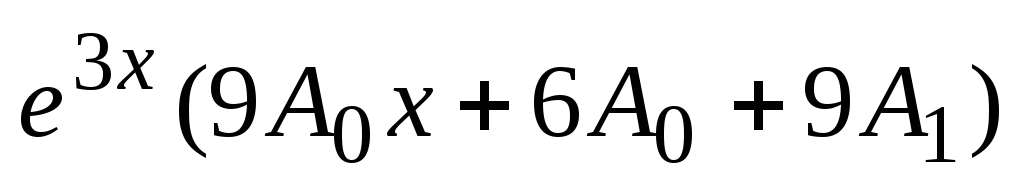 +
+,
+
+,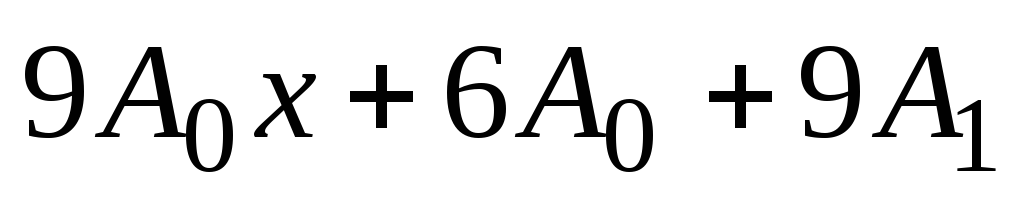 +,.
+,.
Izenačite koeficiente pri 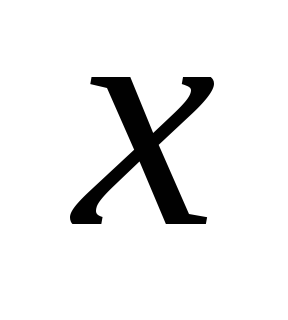 in brezplačni člani:
in brezplačni člani:
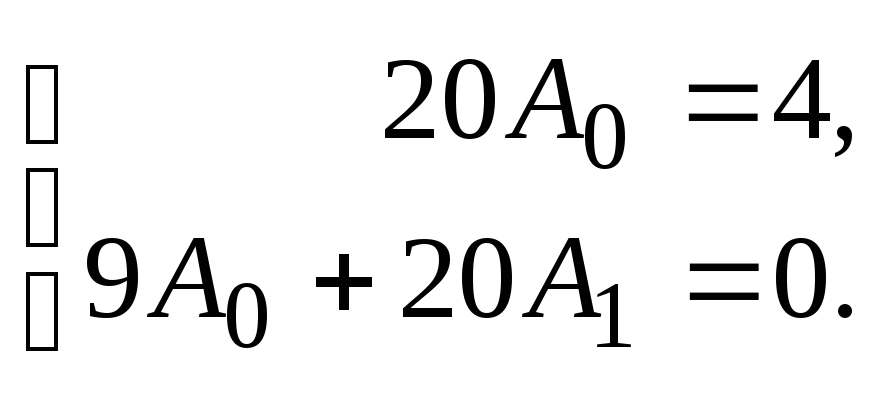 Od tod
Od tod 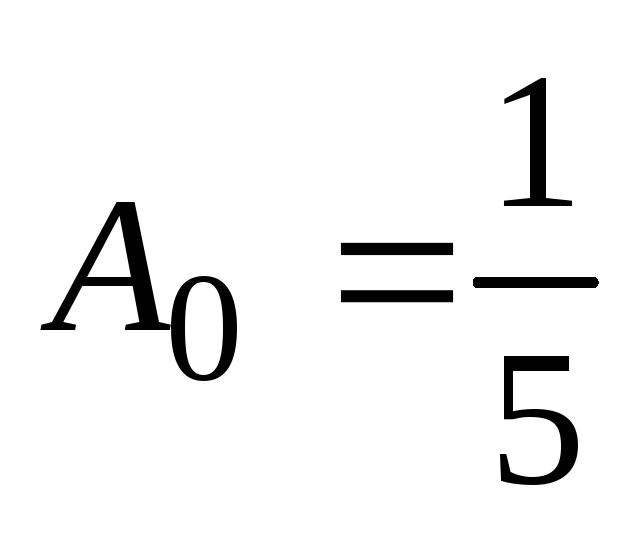 ,
,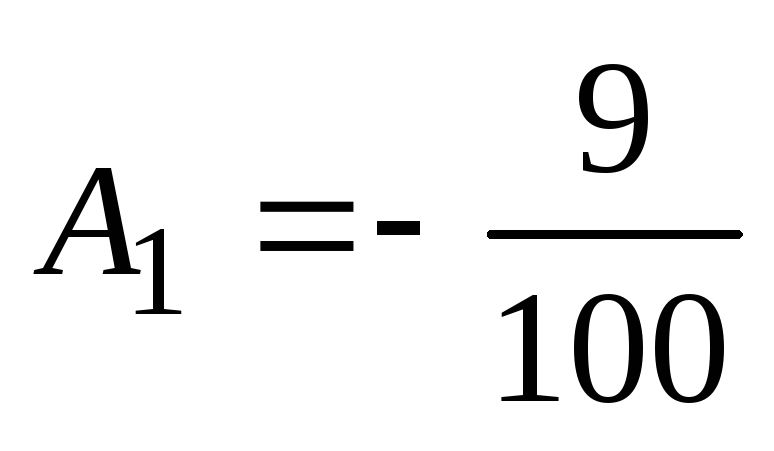 . Potem ima določena rešitev te enačbe obliko
. Potem ima določena rešitev te enačbe obliko 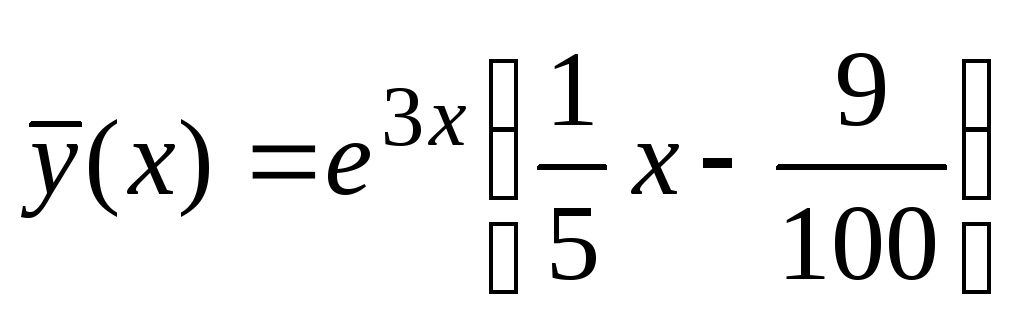 in splošna rešitev
in splošna rešitev
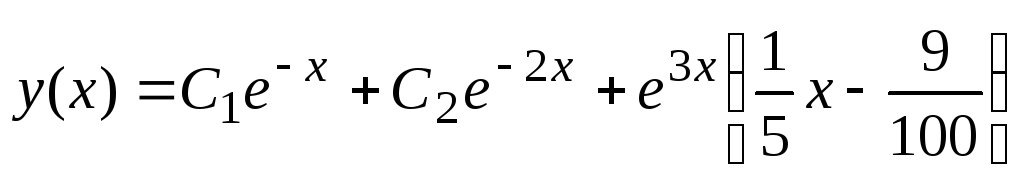 .
.
Lagrangeova metoda variacije poljubnih konstant
Metodo variacije poljubnih konstant lahko uporabimo za katero koli nehomogeno linearno enačbo s konstantnimi koeficienti, ne glede na obliko desne strani. Ta metoda omogoča, da vedno najdemo splošno rešitev nehomogene enačbe, če je znana splošna rešitev ustrezne homogene enačbe.
Pustiti 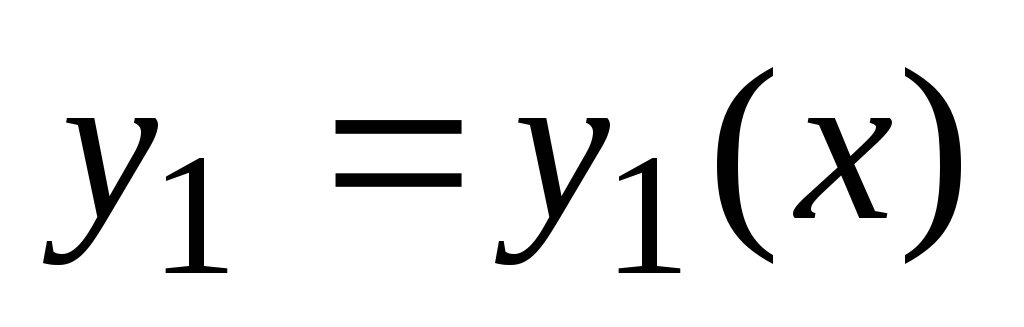 in
in 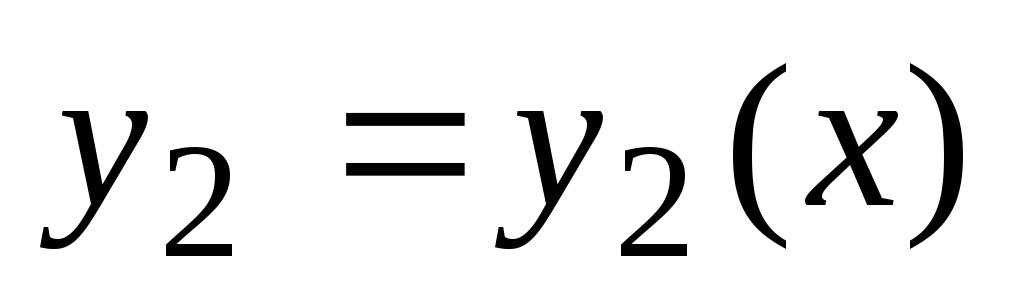 so linearno neodvisne rešitve enačbe (2). Potem je splošna rešitev te enačbe
so linearno neodvisne rešitve enačbe (2). Potem je splošna rešitev te enačbe 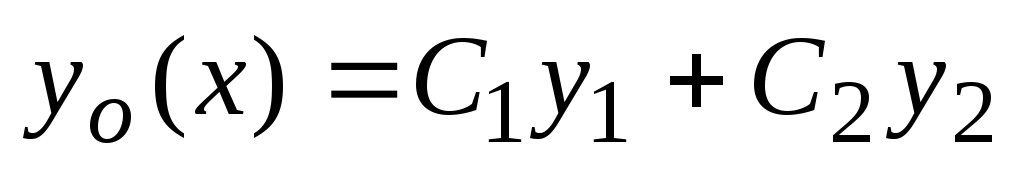 , kje
, kje 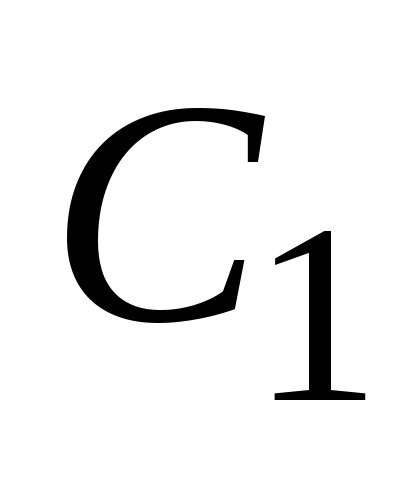 in
in  so poljubne konstante. Bistvo metode variacije poljubnih konstant je v tem, da splošno rešitev enačbe (1) iščemo v obliki
so poljubne konstante. Bistvo metode variacije poljubnih konstant je v tem, da splošno rešitev enačbe (1) iščemo v obliki
kje 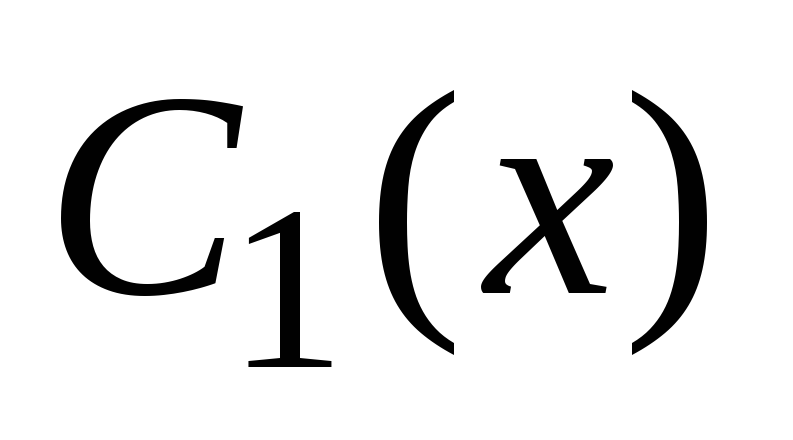 in
in 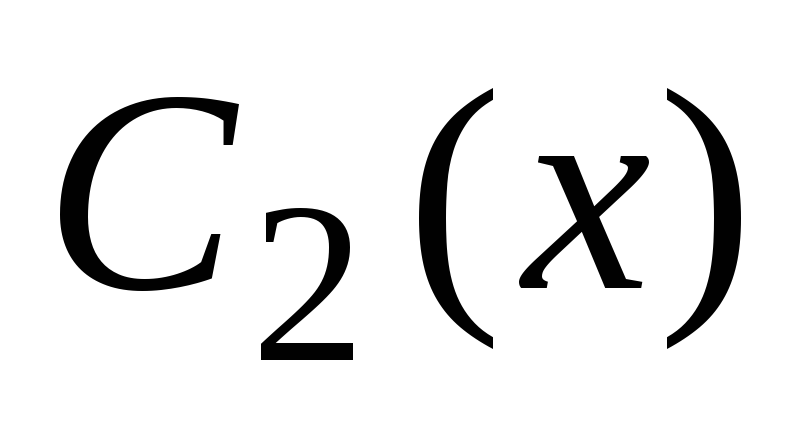 - nove neznane lastnosti, ki jih je treba najti. Ker obstajata dve neznani funkciji, sta za njuno iskanje potrebni dve enačbi, ki vsebujeta ti funkciji. Ti dve enačbi tvorita sistem
- nove neznane lastnosti, ki jih je treba najti. Ker obstajata dve neznani funkciji, sta za njuno iskanje potrebni dve enačbi, ki vsebujeta ti funkciji. Ti dve enačbi tvorita sistem
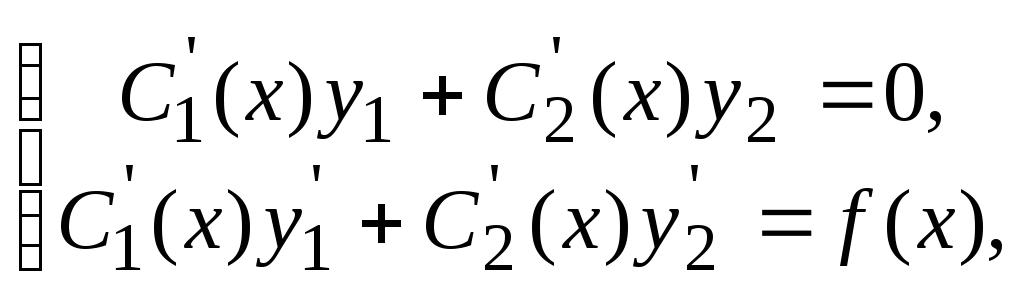
ki je linearni algebrski sistem enačb glede na 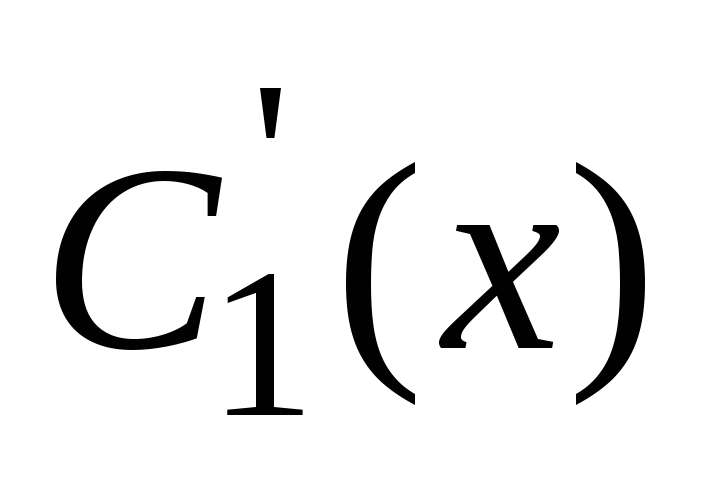 in
in 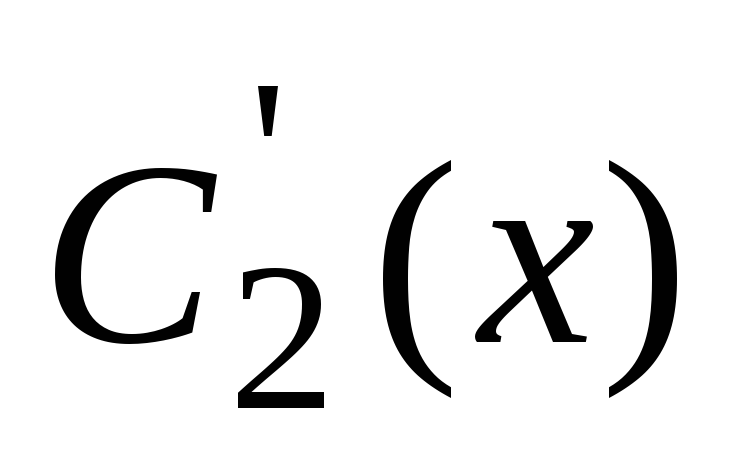 . Reševanje tega sistema, ugotovimo
. Reševanje tega sistema, ugotovimo 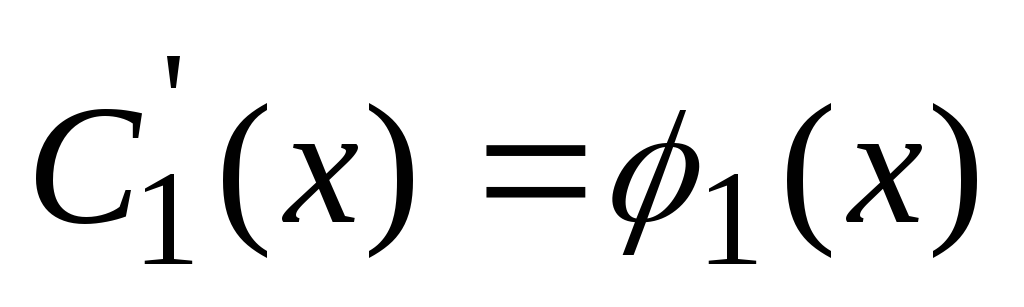 in
in 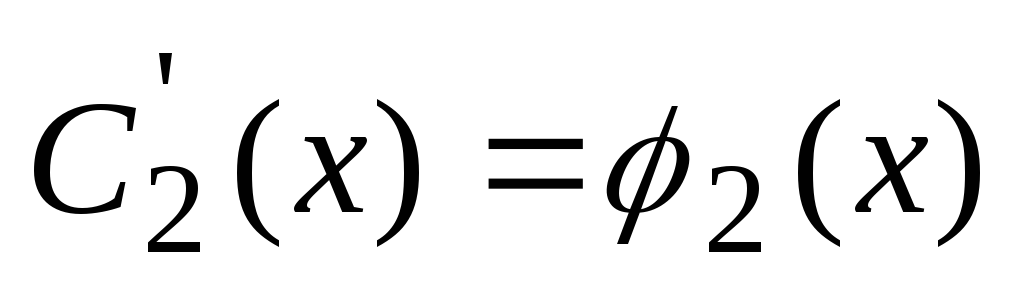 . Z integracijo obeh delov dobljenih enakosti ugotovimo
. Z integracijo obeh delov dobljenih enakosti ugotovimo
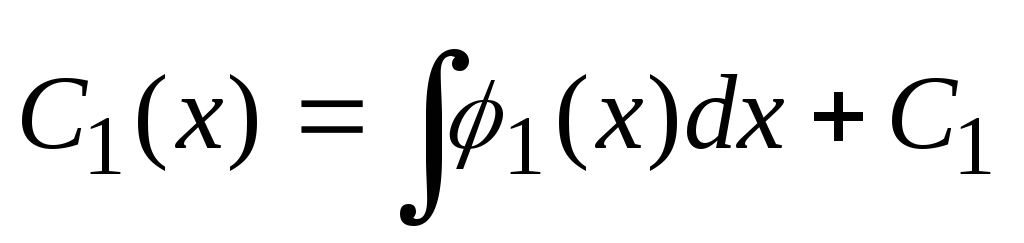 in
in 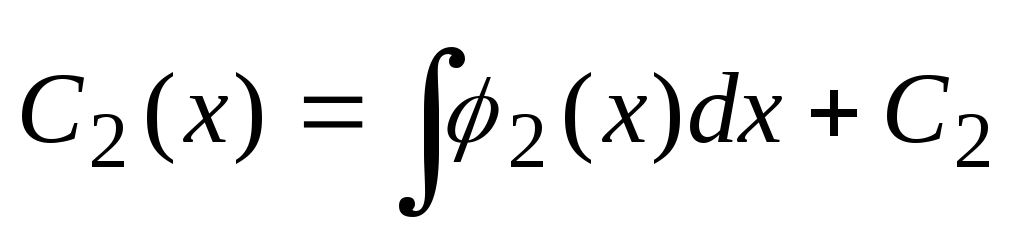 .
.
Če te izraze zamenjamo v (9), dobimo splošno rešitev nehomogene linearne enačbe (1).
Primer 9
. Poiščite splošno rešitev diferencialne enačbe 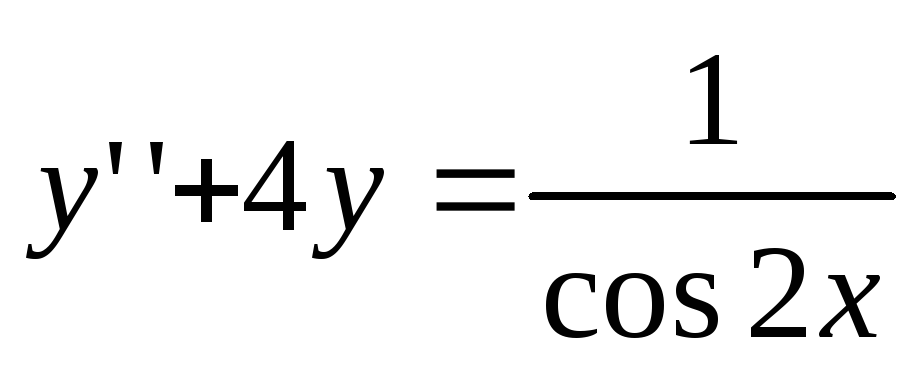 .
.
Rešitev.
Karakteristična enačba za homogeno enačbo, ki ustreza dani diferencialni enačbi, je 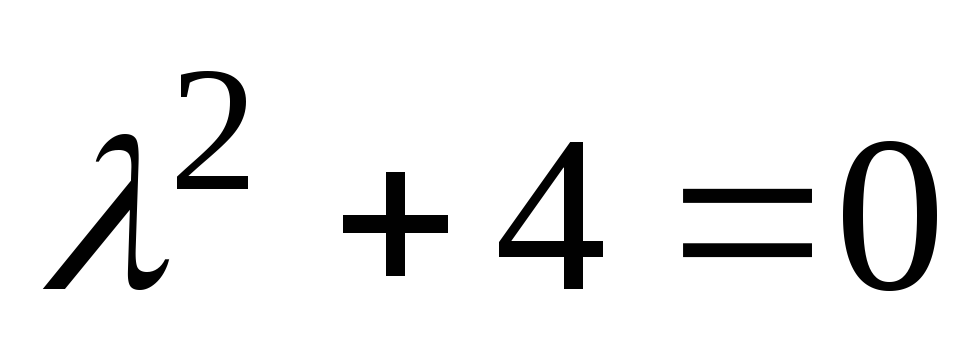 . Njegove korenine so kompleksne
. Njegove korenine so kompleksne 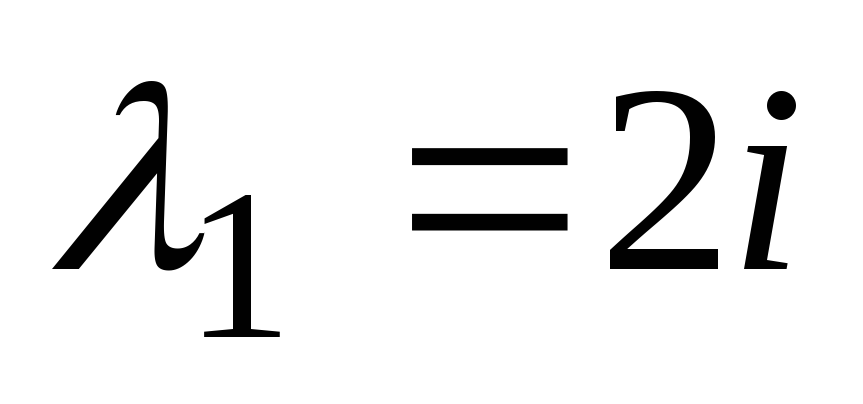 ,
,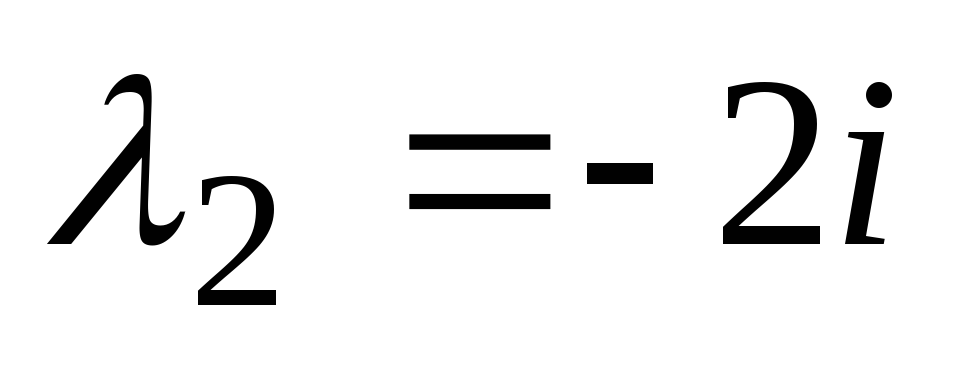 . Ker
. Ker 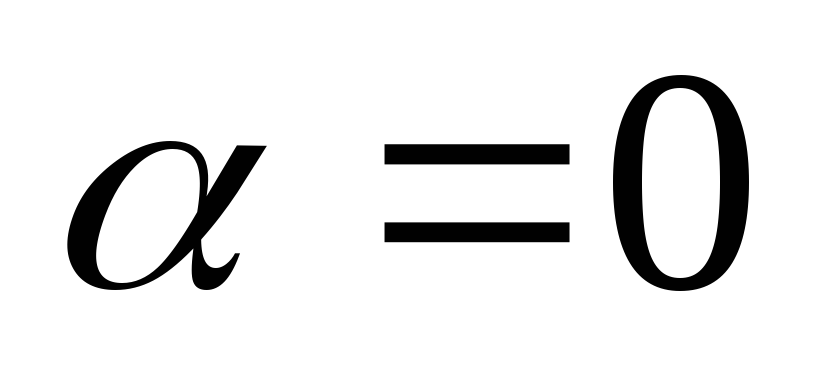 in
in 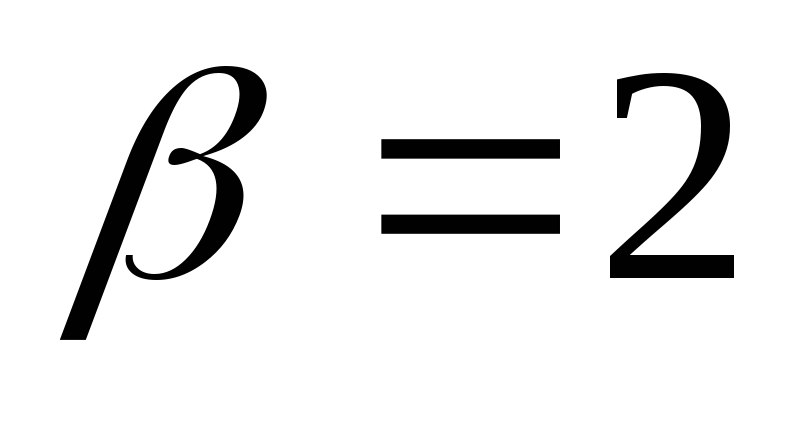 , potem
, potem 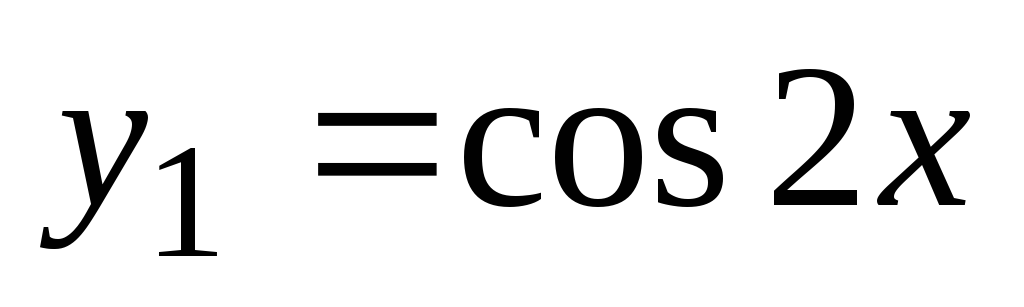 ,
,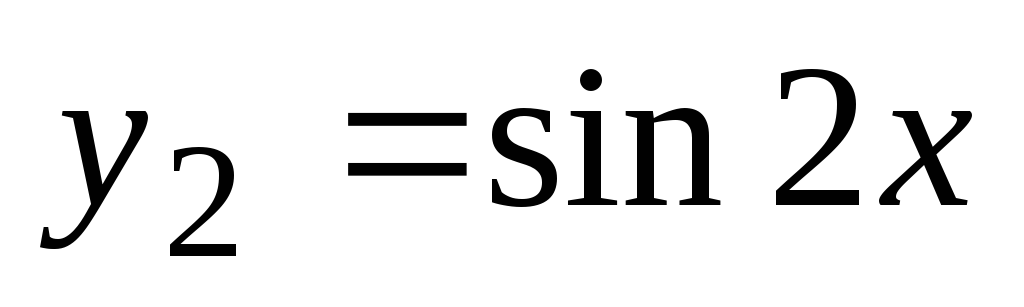 , splošna rešitev homogene enačbe pa ima obliko Potem bomo splošno rešitev te nehomogene enačbe iskali v obliki kjer je
, splošna rešitev homogene enačbe pa ima obliko Potem bomo splošno rešitev te nehomogene enačbe iskali v obliki kjer je 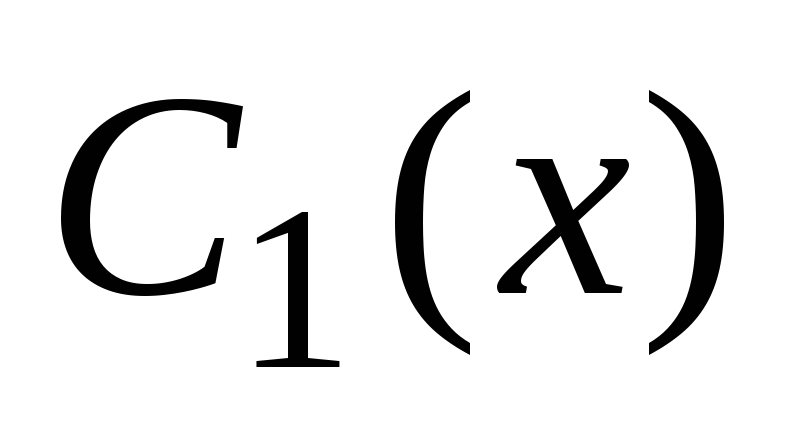 in
in 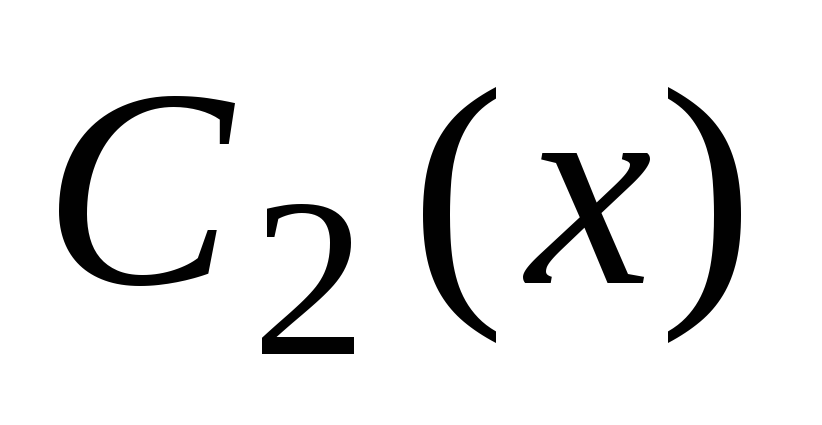 - neznane funkcije.
- neznane funkcije.
Sistem enačb za iskanje teh neznanih funkcij ima obliko
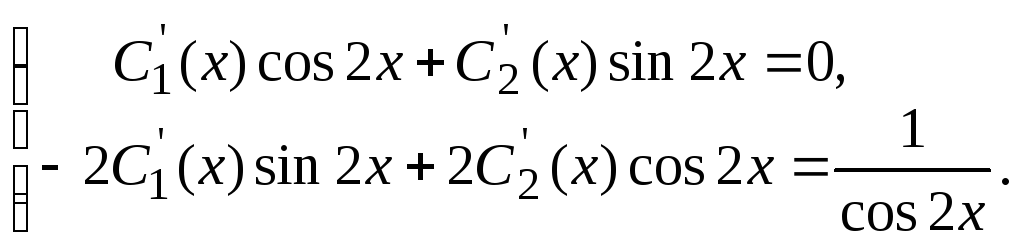
Reševanje tega sistema, ugotovimo 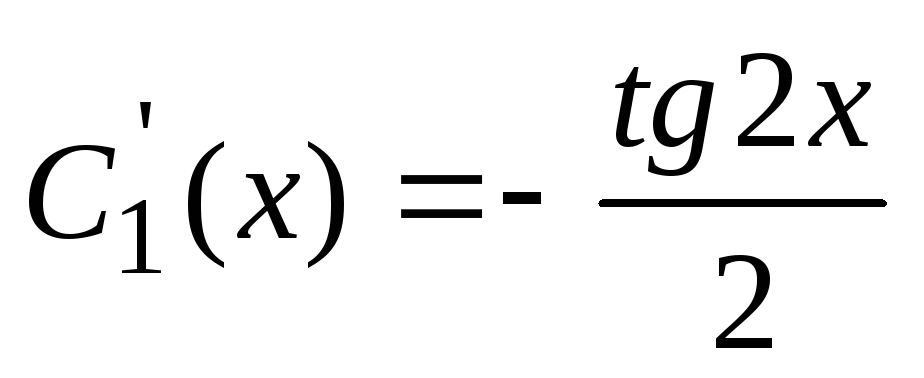 ,
,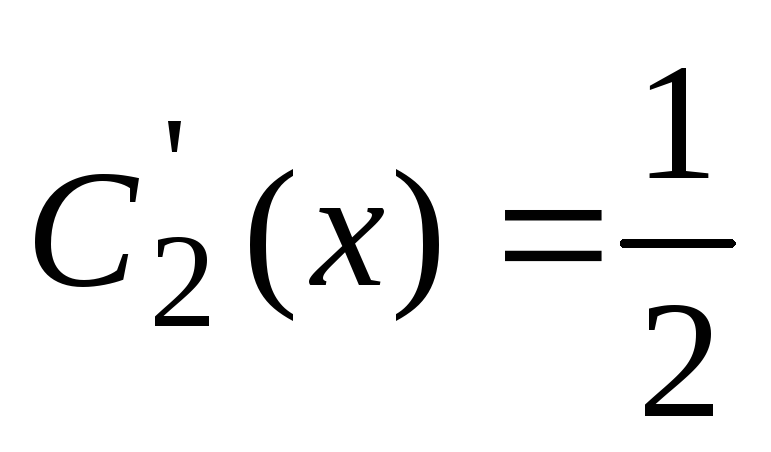 . Potem
. Potem
,
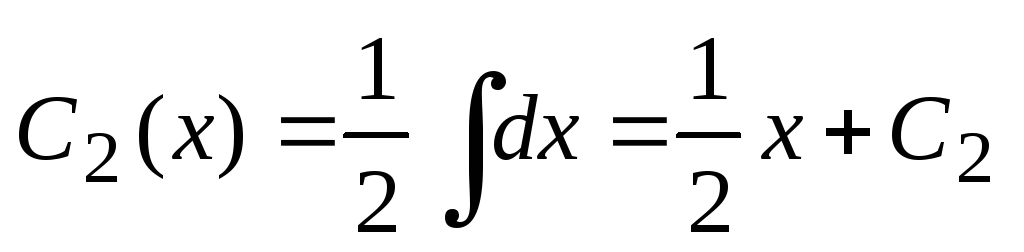 . Dobljene izraze nadomestimo v splošno formulo rešitve:
. Dobljene izraze nadomestimo v splošno formulo rešitve:
To je splošna rešitev te diferencialne enačbe, pridobljena z Lagrangeovo metodo.
Vprašanja za samokontrolo znanja
Katero diferencialno enačbo imenujemo linearna diferencialna enačba drugega reda s konstantnimi koeficienti?
Katero linearno diferencialno enačbo imenujemo homogena in katero nehomogeno?
Kakšne so lastnosti linearne homogene enačbe?
Katero enačbo imenujemo značilna za linearno diferencialno enačbo in kako jo dobimo?
V kakšni obliki je zapisana splošna rešitev linearne homogene diferencialne enačbe s konstantnimi koeficienti v primeru različnih korenov karakteristične enačbe?
V kakšni obliki je zapisana splošna rešitev linearne homogene diferencialne enačbe s konstantnimi koeficienti v primeru enakih korenin karakteristične enačbe?
V kakšni obliki je zapisana splošna rešitev linearne homogene diferencialne enačbe s konstantnimi koeficienti v primeru kompleksnih korenov karakteristične enačbe?
Kako se zapiše splošna rešitev linearne nehomogene enačbe?
V kakšni obliki se išče določena rešitev linearne nehomogene enačbe, če so koreni značilne enačbe različni in niso enaki nič, desna stran enačbe pa je polinom stopnje m?
V kakšni obliki se išče določena rešitev linearne nehomogene enačbe, če je med koreni značilne enačbe ena ničla, desna stran enačbe pa je polinom stopnje m?
Kaj je bistvo Lagrangeove metode?



