1. naloga Telovadnica ima obliko pravokotnega paralelepipeda z osnovo 16 x 25 metrov in višino 8 metrov. Dvorana ima 8 oken dimenzij 4 m x 3 m in dvoja vrata dimenzij 2 m x 2,5 m. Na stene dvorane je potrebno nanesti poseben premaz. Poiščite stroške teh del v tisočih rubljev, če kvadratni meter premaza stane 200 rubljev, morate kupiti premaz z maržo 10%, stroški premaza pa znašajo 70% stroškov nanesenega premaza. .

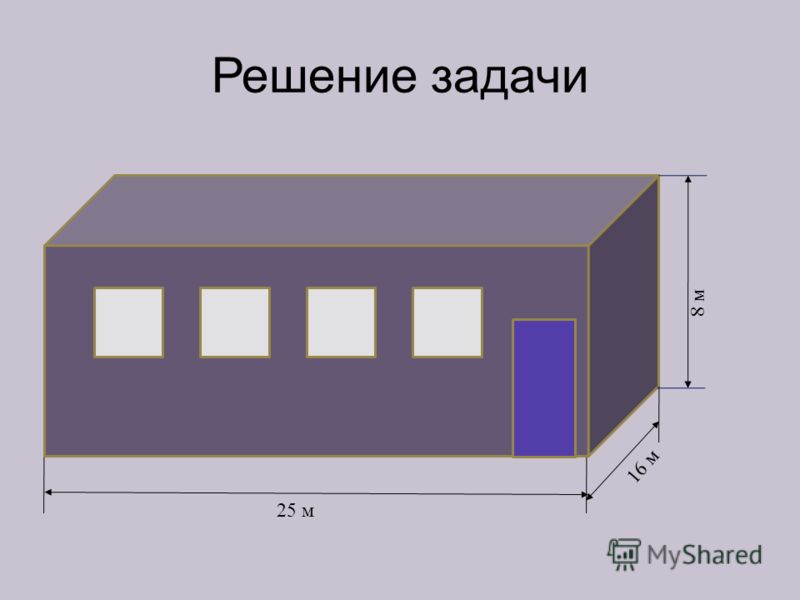
S stene \u003d 82 8 \u003d 656 m²; S okna \u003d 8 4 Z \u003d 96m²; S vrata \u003d 2 2 2,5 \u003d 10m². Tako je pokrita površina 656m² - 96m² - 10m² = 550m². Stroški premaza, nanesenega na stene, so enaki = rub. Stroški dela so 70% stroškov nanesenega premaza, potem je enak 0, = 77.000 rubljev. Morate kupiti pokritost z maržo 10%, skupni stroški materiala (vključno z maržo) 1, \u003d 121OOOrub, stroški so \u003d rubljev. Odgovor mora biti napisan v tisočih rubljev, to je 198 tisoč rubljev. Odgovor: 198

2. naloga Dvorana z bazenom ima obliko pravokotnega paralelepipeda z osnovo 30 x 50 metrov in višino 10 metrov. Dvorana ima 6 oken dimenzij 8 m x 5 m in štiri vrata dimenzij 3 m x 2,5 m. Na stene dvorane je potrebno nanesti poseben premaz. Poiščite stroške teh del v tisočih rubljev, če kvadratni meter premaza stane 100 rubljev, morate kupiti premaz z maržo 5%, stroški premaza pa znašajo 80% nanesenega premaza. Zaokrožite svoj odgovor na najbližjih tisoč rubljev, pri čemer zavrzite ulomek.

Naloga 3 Za lepljenje sten sobe morate kupiti tapete, širina sobe je 4 m, dolžina 5 m in višina 3 m. Prostor ima okno dimenzij 3 m x 2 m in vrata dimenzij 1,05 m x 2 m, dolžina rola tapete je 10,5 m, širina 0,6 m in neizkoriščene ozke pasove. Poiščite najmanjše število zvitkov tapet, ki jih morate kupiti, da pokrijete sobo.

4. naloga Hladilnik ima obliko pravilne štirikotne prizme, katere višina je 2-kratna stranica podnožja. V hladilnik smo postavili škatlo v obliki pravokotnega paralelopipeda z dimenzijami 20 cm x 20 cm x 50 cm in še dve škatli v obliki kocke s stranico 20 cm, kar je povzročilo 1,8 % prostornina hladilnika je bila zasedena. Poiščite višino hladilnika (v cm).


Ker ima hladilnik obliko pravilne štirikotne prizme, katere višina je 2-kratna stranica podnožja, je osnova hladilnika kvadrat s stranico x cm, višino 2x cm.V hladno. =a b c = x x 2x = 2x³ cm³. V 1 škatel = = 20000 cm³, V 2 škatel = = 8000 cm ³, Prostornina škatel v hladilniku je V = = cm³, kar je 1,8 % prostornine hladilnika. Zato je 2х³=; x³=; x = 100. Odgovor: 200

5. naloga Plesna dvorana ima obliko pravokotnega paralelepipeda z osnovo 8 m x 12 m in višino 5 metrov. Dvorana ima dva stebra od tal do stropa, katerih presek je kvadrat s stranico 0,8 m.Tla in stebre je potrebno obložiti s ploščicami. Poiščite minimalno število kvadratnih metrov ploščic, ki jih morate kupiti, če gre 10 % kupljenih ploščic v nič.

6. naloga Sprejemna dvorana ima obliko pravokotnega paralelepipeda z osnovo 20 m x 30 m in višino 10 metrov. Dvorana ima 4 stebre od tal do stropa, katerih presek je kvadrat s stranico 2 metra. Na tla in stebre je potrebno nanesti oblogo iz ploščic. Določite, koliko kvadratnih metrov ploščic morate kupiti, če želite imeti zalogo ploščic v višini 15 % minimalne zahtevane količine. Odgovor zaokrožite na najbližje celo število.

Problem 7 Na sliki je prikazana skica stopničk, vse dolžine so v cm, širina vsake od treh stopnic (za "zlate", "srebrne" in "bronaste" medalje) je enaka. Ta podstavek je treba obložiti z letvami iz mahagonija, vsaka 1 m dolga in 10 cm široka. Poiščite število tirnic, ki jih morate kupiti za to, če želite, da je zaloga tirnic vsaj 10% minimalne zahtevane količine.

Rešitev problema Če želite najti zahtevano število tirnic, morate celotno površino podstavka razdeliti na površino ene tirnice in dodati 10% dobljenega števila. S tirnice = 10010 = 1000 cm² S zgor =60 ()=15000cm² S stran =() 2=10000cm² S polna površina \u003d \u003d 25000 cm² n \u003d 25000 / 1000 \u003d 25; 10 % od 25 je 2,5, tj. 3 letvice Odgovor: 28

8. naloga Na sliki je skica računalniške mize (vse dolžine so v cm). Vsi elementi strukture mize imajo enako debelino, enako 1 cm, in so izdelani iz istega materiala, katerega gostota je 2000 kg/m³. Izračunajte maso te tabele (v kg), pri čemer zanemarite vpliv debeline stene na dimenzije, navedene na skici.
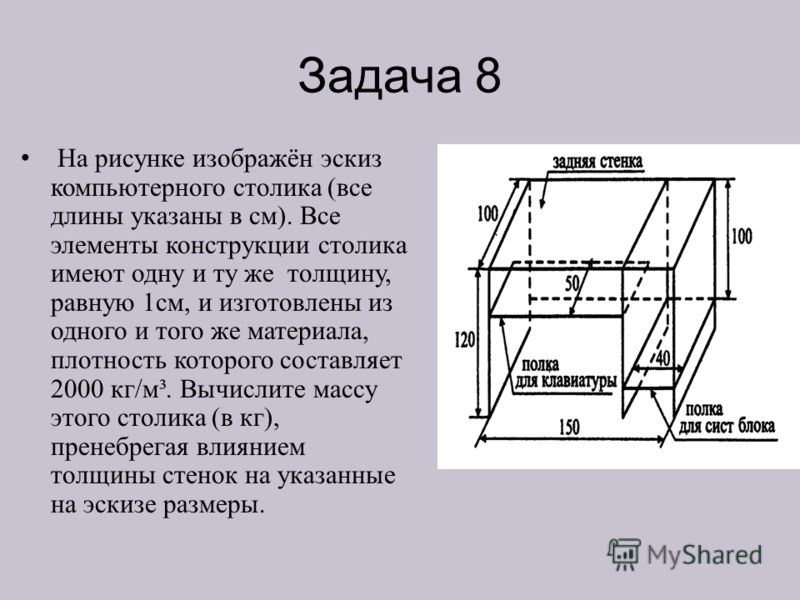
Rešitev problema Če želite izračunati maso računalniške mize, morate površino vseh elementov zasnove mize pomnožiti z 0,01 m in pomnožiti z 2000 kg / m³. S stran art. =1,2 1 3=3,6 m² S zadnja stena =1,5 1=1,5 m² S polica za tipkovnico =1,1 0,5=0,55m² S polica sistemske enote =0,4 1=0,4m² S zgornja miza =1,5 1= 1,5 m² S skupaj \u003d 3,6 + 1,5 + 0,55 + 0,4 + 1,5 \u003d 7,55 m² m \u003d 7,550, \u003d 151 kg Odgovor: 151

Naloga 9 Po projektu naj bi imela hiša obliko pravokotnika dimenzij 12 m x 8 m, višino sten 3 m, šest oken dimenzij 2 m x 1,5 m in vrata dimenzij 1,2 m x 2,5 m. Za konstrukcijo zunanjih sten je predvidena opeka 5 cm x 20 cm x 10 cm Stene hiše morajo imeti debelino 20 cm Poiščite število tisoč opek, ki jih je treba kupiti za gradnjo sten hiše. hišo, če je zahtevano, da se opeka kupi z maržo vsaj 10% minimalne zahtevane količine (odgovor zaokrožite na najbližje celo število).

10. naloga Zasebna hiša ima obliko pravokotnika z merami 10 m x 8 m.Višina zunanjih sten hiše je 3 m, njihova debelina pa 20 cm. Izračunajte maso zunanjih sten hiše, če je znano, da ima hiša šest oken 2 m x 1,5 m in vrata 1 m x 2,5 m, gostota materiala sten pa je 4000 kg/m³. Svoj odgovor izrazite v tonah. Odgovor: 70

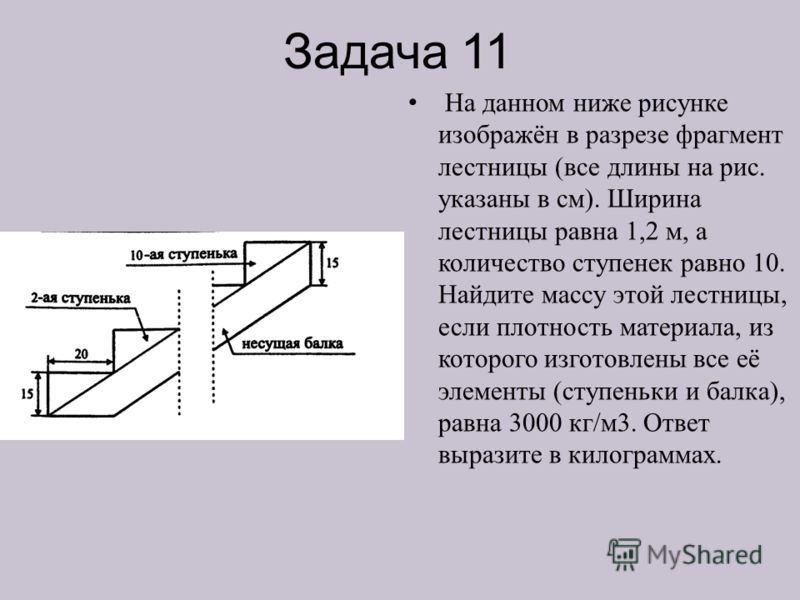
Naloga 11 Na spodnji sliki je delček lestve v prerezu (vse dolžine na sliki so navedene v cm). Širina stopnišča je 1,2 m, število stopnic pa 10. Poiščite maso tega stopnišča, če je gostota materiala, iz katerega so izdelani vsi njegovi elementi (stopnice in nosilec), 3000 kg/m3. Odgovor izrazite v kilogramih.
12. naloga Spodnja slika prikazuje prerez površja umetnega slapu (vse dolžine na sliki so v cm). Višina in kot naklona vsakega od "stopnic" sta enaka, enaka je tudi dolžina vsakega od vodoravnih odsekov. Širina slapu je 5 m Izračunaj prostornino prostora pod gladino slapa. Odgovor izrazite v kubičnih metrih.

13. naloga Škatla ima obliko pravokotnega paralelepipeda z merami 20 cm x 18 cm x 15 cm. Določite največje število takšnih škatel, ki jih lahko postavite v kvadrasto škatlo 110 cm x 40 cm x 25 cm, ob predpostavki, da je katera koli stena vsake od škatel vzporedna z eno od sten škatle. Odgovor: 14 Naloga 14 Škatla ima obliko kvadra z merami 1,8 m x 1,5 m x 1,2 m Določite največje število takšnih škatel, ki jih lahko postavite v hangar, ki ima obliko kvadra z merami 10 m x 3,5 m x 2,2 m, če predpostavimo, da je katera koli stena vsakega od boksov vzporedna z eno od sten hangarja. Odgovor: 16

Ste že slišali za dvojno sklopko, dragi motorist? Menjalnik z dvojno sklopko niso sanje ali fantazija iz znanstvenofantastičnega filma. se že dolgo uspešno uporablja na različnih modelih avtomobilov. To načelo združuje prednosti in prednosti dveh vrst menjalnikov - "avtomatsko" in "mehaniko". Kombinirani menjalnik je najboljše, o čemer lahko voznik sanja. V tem članku bomo natančno preučili, v katerih prednostih se takšna škatla razlikuje, ali so v njej kakšne pomanjkljivosti in kako se je začela zgodovina njenega ustvarjanja.
Dvojna škatla ni samo. Tak prenos je bil uspešno ustvarjen in združuje veliko prednosti, o katerih bomo podrobneje razpravljali v nadaljevanju. Omeniti velja, da je čas, v katerem takšna škatla prestavi, le osem milisekund, kar je neverjeten rezultat.
Zgodovina nastanka takšne sklopke
Pravzaprav ideja o ustvarjanju menjalnika z dvema sklopkama pripada slavnemu oblikovalcu Adolfu Kegressu. To idejo je oblikoval tako, da je komisiji v pregled predložil samodejni menjalnik z dvojno sklopko. Njeno, to isto kontrolno točko, je inženir upal namestiti na Traksion. Toda depresivno finančno stanje podjetja v tistem času ni omogočilo uresničitve načrta.
Minilo je nekaj časa in tega odkritja se spominjata priljubljena avtomobilska koncerna Audi in. Toda spet zaradi nekih nerazumljivih dejavnikov takšne kontrolne točke niso upali namestiti na navadne avtomobile. A dvojno sklopko so uspešno krstili na dirkalnikih. Leta 1986 je Porsche 962, opremljen s to posebno škatlo, zmagal na 1000 km dolgi dirki v Monzi.

Kar se tiče vgradnje prvega avtomatskega menjalnika z dvojno sklopko na običajnih avtomobilih, so se proizvajalci legendarnega koncerna odločili obvladati novost. To je njihova vrsta menjalnika. Danes so avtomobili, kot so Volkswagen Golf, Jetta, Audi TT, Škoda Octavia in številni drugi modeli in znamke opremljeni z dvojno sklopko.
Vrste škatel, ki se danes uporabljajo
Do danes so znane naslednje vrste škatel: ročni menjalnik, robotski menjalnik, menjalnik z dvojno sklopko, CVT. Če je o ročnem menjalniku veliko znanega in je takšna škatla doslej najpreprostejša, potem bomo upoštevali vse ostale.
Klasični avtomatski menjalnik

Klasični samodejni menjalnik, ki se danes uporablja v številnih avtomobilih, se nedvomno razlikuje od svojih predhodnikov. Najprej je to število razponov in sam princip nadzora škatle. Če prej s štirimi ali manj prestavami, se je danes njihovo število povečalo, za krmiljenje pa je zaslužna elektronika, čeprav je prej za to skrbela hidravlika. Poleg tega skoraj vsi sodobni avtomobili, opremljeni s samodejnim menjalnikom, uporabljajo sistem zaklepanja pretvornika navora, nekatere škatle pa imajo celo funkcijo ročnega preklopa območja.
Jasno je, da ima sodoben samodejni menjalnik veliko prednosti pred starejšimi različicami. To je tako mehko, ki ga voznik in potniki skoraj ne čutijo, prestavljanje v primestnem načinu vožnje in bolj enakomerno prestavljanje pri kateri koli vrednosti navora, kar je prednost, tudi če primerjamo samodejni menjalnik z ročnim menjalnikom.
Osempasovni avtomatski menjalnik ZF 8HP z obdarjenim sistemom Start / Stop danes velja za najboljšega. Dinamika in tehnične komponente najboljšega avtomatskega menjalnika na svetu se praktično ne razlikujejo od ročnega menjalnika, v nekaterih primerih pa ga celo prekašajo. Če to škatlo primerjamo z drugimi avtomatskimi škatlami, jih prekaša in je kar 20% nižja.
Robotska kontrolna točka
Video pove, kaj je robotski menjalnik:
Skoraj "mehanika", le robot. V takšni škatli so servo in hidravlični pogoni, ki uspešno nadzorujejo delovanje sklopke in prestave. Visok izkoristek, neposreden prenos navora na kolesne pogone in še veliko več so glavne prednosti tega tipa menjalnika.
Nič manj priljubljen je proizvajalec FiatPowertrainTechnologies, ki proizvaja najboljše suhe sklopke z visokim navorom.
Ločeno bi rad izpostavil tudi FEVGmbH, proizvajalca, ki se osredotoča na zmanjšanje kompleksnosti enot in poskuša poenostaviti vse zaradi teže in velikosti.
Za konec še proizvajalec Getrag, ki izdeluje odlične dvosklopčne menjalnike, ki veljajo za najbolj okolju prijazne. Takšne škatle kot druge.
Poleg zgoraj opisanih proizvajalcev dvojnih zabojev so znani še Ricardo, Graziano, Luk in drugi.
Menjalnik z dvojno sklopko danes upravičeno velja za enega najboljših. Številni proizvajalci avtomobilov že prehajajo na proizvodnjo modelov, ki imajo ravno takšno škatlo, za katero je značilna visoka hitrost in gladko prestavljanje.
Naloga 13 (osnovna raven)
Na dnu ravne prizme leži pravokotni trikotnik s krakoma 6 in 8. Stranski robovi prizme so enaki 6/Pi. Poiščite prostornino valja, ki ga oklepa ta prizma.
Valj in stožec imata skupno osnovo, vrh stožca leži na osi valja, višina stožca se glede na višino valja nanaša v razmerju 3:4. Poišči prostornino valja, če je prostornina stožca 30.
Središče roba kocke s stranico 1,9 je središče krogle s polmerom 0,95. Poiščite ploščino S dela površine krogle, ki leži znotraj kocke. V odgovor napišite S/Pi.
Konci segmenta KM ležijo na krogih baz valja. Višina valja je 24, polmer osnove je 13, kot med premico KM in ravnino osnove valja pa je 60°. Poiščite razdaljo med osjo valja in z njo vzporedno ravnino, ki poteka skozi točki K in M.
AT kvader Znane so dolžine robov ABCDA1B1C1D1: AB = 8, AD = 9, AA1 = 12. Poiščite razdaljo med oglišči A in C1 tega polja.
Stranski rob pravilne trikotne prizme je sqrt (3), skupna površina prizme pa je 36 sqrt (3). Poiščite stranico osnove prizme.
V trikotni piramidi SABC delijo točke N in M, P in Q, K in L ustrezne stranske robove na 3 enake dele. Prostornina politopa NLQMKP je 21. Poiščite prostornino piramide SABC. 
Območje stranske ploskve pravilne trikotne piramide SABC je 72, območje celotne ploskve piramide SMNQ, odrezano od prve ravnine, ki je vzporedna z osnovo in poteka skozi sredino višine, je 24. Poiščite ploščino trikotnika ABC. 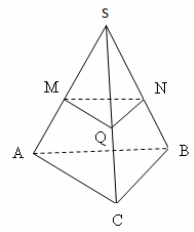
Poiščite stransko površino stožca, včrtanega v pravilno trikotno piramido z vsemi robovi, enakimi 6sqrt(2).
(V odgovor napišite S_(stran)/Pi)
V valjasti posodi nivo tekočine doseže 98 cm. Na kakšni višini bo tekočina, če jo vlijemo v drugo valjasto posodo, katere premer je 7-krat večji od premera prve. Odgovor izrazi v centimetrih. 
odgovor: preveriti
Površina stranske površine stožca je 10 cm^2. Polmer osnove stožca se je povečal za 6-krat, generatrisa pa se je zmanjšala za 4-krat. Poiščite stransko površino nastalega stožca. Podajte svoj odgovor v cm^2.
odgovor: preveriti
Celotna površina tega pravilnega tetraedra je 80 cm^2. Poiščite celotno površino pravilnega tetraedra, katerega rob je 4-krat manjši od danega tetraedra. Podajte svoj odgovor v cm^2.
odgovor: preveriti
Prostornina kocke je 52. Poiščite prostornino trikotne prizme, ki jo odseka ravnina, ki poteka skozi središči dveh robov, ki izhajata iz istega oglišča in je vzporedna s tretjim robom, ki izhaja iz istega oglišča. 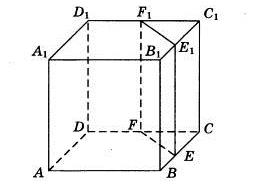
odgovor: preveriti
Pravilna štirikotna prizma je opisana blizu valja, katerega osnovni polmer je 2. Stranska površina prizme je 48. Poiščite višino valja. 
Prostornina pravokotnega paralelepipeda, ki temelji na kvadratu, je 16 cm^2. Drugi pravokotni paralelepiped, ki ima na dnu tudi kvadrat, ima štirikrat manjšo višino, osnovni rob pa je dvakrat večji od prvega. Poiščite prostornino drugega kvadra (v kubičnih centimetrih).
odgovor: preveriti
V stožčasto posodo, do vrha napolnjeno s tekočino, katere prostornina je 160 ml, smo odprli pipo in tekočino izlili do nivoja (1/2) višine. Sk. mililitrov tekočine, izlite iz posode? 
Nivo tekočine v valjasti posodi doseže 180 cm. Na kakšni višini bo gladina tekočine, če jo vlijemo v drugo valjasto posodo, katere osnovni premer je 2-krat večji od premera prve? Odgovor izrazite v cm.
odgovor: preveriti
Pravilna štirikotna piramida z robom 1 je prilepljena na kocko z robom 1 tako, da kvadratni ploskvi sovpadata. Koliko robov ima nastali polieder (nevidni robovi na sliki niso prikazani)? 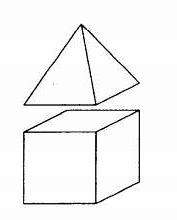
odgovor: preveriti
Iz lesene pravilne trikotne prizme so bila odžagana vsa njena oglišča (glej sliko). Koliko oglišč ima nastali polieder (nevidni robovi na sliki niso prikazani)? 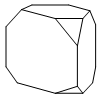
Valj je vpisan v stožec tako, da njegova spodnja osnova leži v ravnini osnove stožca, zgornja osnova pa se dotika vsake generatrise stožca in seka višino stožca v njegovi sredini. Poiščite prostornino stožca, če je prostornina valja 45. 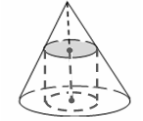
Škatla v obliki kocke z robom 20 cm brez ene ploskve mora biti pobarvana z vseh strani od zunaj. Poiščite površino površine, ki jo želite pobarvati. Odgovor zapišite v kvadratnih centimetrih.
V kvadru ABCDAA1B1C1D1 AA1=4, AB=6, AD=sqrt(10). Poiščite površino prečnega prereza paralelepipeda z ravnino A1MK, kjer sta točki M in K razpolovišči robov BB1 oziroma CC1.
V posodi stožčaste oblike nivo tekočine doseže 1/2 višine. Prostornina tekočine je 25 ml. Koliko mililitrov tekočine je treba dodati, da se posoda popolnoma napolni? 
Prostornina kozarca, ki ima obliko stožca, je 20 ml. Starši so natočili poln kozarec napitka in prepričali nepopustljivega Serjožo, naj popije vsaj "pol", tj. tako da je po tem nivo preostale tekočine 1/2 višine. Koliko mililitrov mešanice je popil Serjoža? 
odgovor: preveriti
Rezervoar v obliki valja je napolnjen s 5 litri vode. Ko je bil del popolnoma potopljen v vodo, se je nivo vode v rezervoarju povečal za 2,8-krat. Poiščite prostornino dela. Odgovorite v kubičnih centimetrih, pri čemer veste, da je v enem litru 1000 kubičnih centimetrov. 
Piramida Menkaure ima obliko pravilne štirikotne piramide, katere stranica dna je 102 m, višina pa 66 m. Stran dna natančne muzejske kopije te piramide je 34 cm. Poiščite višina muzejske kopije. Odgovorite v centimetrih.
Voda v valjasti posodi je na višini h = 80 cm.Na kolikšni višini bo voda, če jo prelijemo v drugo valjasto posodo, katere polmer podnožja je štirikrat večji od danega? Odgovorite v centimetrih. 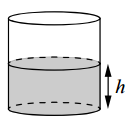
odgovor: preveriti
Območje stranske površine trikotne prizme je 24. Skozi srednjo črto osnove prizme je narisana ravnina, vzporedna s stranskim robom. Poiščite površino stranske površine odrezane trikotne prizme. 
odgovor: preveriti
V posodo, ki ima obliko ravne prizme, nalijemo 5 litrov vode. Ko je bil del popolnoma potopljen v vodo, se je nivo vode v rezervoarju povečal za 1,4-krat. Poiščite prostornino dela. Odgovorite v kubičnih centimetrih, pri čemer veste, da je v enem litru 1000 kubičnih centimetrov. 
odgovor: preveriti
Valj in stožec imata skupno osnovo in višino. Višina valja je enaka polmeru osnove. Bočna površina valja je 23 kvadratnih metrov (2). Poiščite površino stranske površine stožca.
odgovor: preveriti
Od trikotne piramide, katere prostornina je enaka 12, je trikotna piramida odrezana z ravnino, ki poteka skozi vrh piramide in srednjo črto baze. Poiščite prostornino odrezane trikotne piramide.
Območje osnove stožca je 63. Ravnina, vzporedna z ravnino osnove stožca, deli njegovo višino na segmente dolžine 1 in 2, šteto od vrha. Poiščite površino prečnega prereza stožca s to ravnino. ![]()
odgovor: preveriti
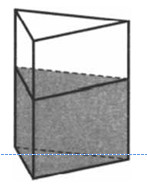
V posodo, ki je imela obliko pravilne trikotne prizme, smo nalili 2500 cm3 vode in del popolnoma potopili vanjo. pri čemer
gladina tekočine v posodi se je dvignila z 20 cm na 31 cm Kolikšna je prostornina dela? Odgovor izrazite v cm^3.
odgovor: preveriti
Khafrenova piramida ima obliko pravilne štirikotne piramide, katere stranica baze je 210 m, višina pa 136 m. Stranica baze natančne muzejske kopije te piramide je 10,5 cm. Poiščite višino muzejska kopija. Odgovorite v centimetrih.
odgovor: preveriti
Keopsova piramida ima obliko pravilne štirikotne piramide, katere stranica baze je 230 m, višina pa 147 m. Stran baze natančne muzejske kopije te piramide je 115 cm. Poiščite višina muzejske kopije. Odgovorite v centimetrih.
odgovor: preveriti
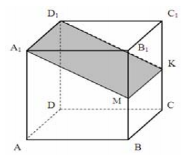
Skozi srednjo črto osnove trikotne prizme (glej sliko 21), katere prostornina je 36, je narisana ravnina, vzporedna s stranskim robom. Poiščite prostornino odrezane trikotne prizme. 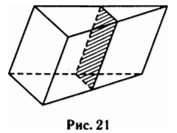
odgovor: preveriti
Litoželezni del smo dali v valjasto posodo in nalili 2000 cm^3 vode. Izkazalo se je, da je nivo tekočine 21 cm. Ko so del vzeli iz posode, je nivo vode padel za 11 cm. Kolikšna je prostornina dela? Odgovor izrazite v cm^3. 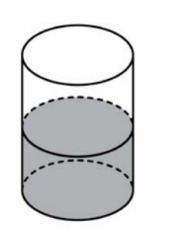
odgovor: preveriti
Za pripravo valjaste torte Maša porabi 400 g moke. Koliko gramov moke mora vzeti Maša, da naredi torto enake oblike, vendar dvakrat ožjo in trikrat višjo?
odgovor: preveriti
Rezervoar v obliki ravne prizme je napolnjen s 6 dm^3 vode. Ko je del popolnoma potopljen v vodo, se višina vodnega stolpca v rezervoarju poveča za 2,5-krat. Poiščite prostornino dela. Odgovorite v kubičnih decimetrih.
V stožčasto posodo nalijemo 10 ml tekočine, nivo tekočine pa doseže 2/5 višine posode. Koliko mililitrov tekočine je treba dodati, da se posoda popolnoma napolni. ![]()
V pravilni trikotni piramidi SABC z osnovo ABC je točka M razpolovišče roba BC, S je vrh. Vemo, da je AB = 6, stranska površina pa je 45. Poiščite dolžino segmenta SM. 
odgovor: preveriti
V stožec sta narisana dva preseka z ravninama, ki sta vzporedni z ravnino osnove stožca. S točkami presečišča teh ravnin z višino stožca je ta razdeljen na 3 enake segmente. Poiščite prostornino srednjega dela stožca, če je prostornina spodnjega dela 38. 
odgovor: preveriti
Rezervoar v obliki ravne prizme je napolnjen s 6 litri vode. Ko je del popolnoma potopljen v vodo, se nivo vode v rezervoarju poveča za 2,5-krat. Poiščite prostornino dela. Odgovorite v litrih.
odgovor: preveriti
V posodi stožčaste oblike nivo tekočine doseže 1/5 višine. Prostornina tekočine je 10 ml. Koliko mililitrov
Ali moram dodati tekočino, da popolnoma napolnim posodo?
odgovor: preveriti
Voda v valjasti posodi je na višini 25 cm. Na kolikšni ravni bo voda, če jo nalijemo v drugo valjasto posodo, katere osnovni polmer je 5-krat večji od polmera prve? Odgovorite v centimetrih.
odgovor: preveriti
V pravilni trikotni piramidi SABC je točka P razpolovišče roba AB, S je oglišče. Vemo, da je SP = 4, stranska površina pa je 24. Poiščite dolžino segmenta BC.
Dvokapna streha hiše s pravokotnikom na dnu (glej sliko) mora biti popolnoma prekrita s strešnim materialom. Višina strehe je 2,5 m, dolžini sten hiše sta 10 m in 12 m Ugotovite, koliko strešnega materiala (v kvadratnih metrih) potrebujete za pokrivanje te strehe, če so nakloni strehe enaki. 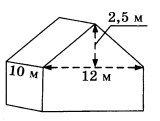
odgovor: preveriti
V valjasti posodi nivo tekočine doseže 192 cm. Na kakšni višini bo nivo tekočine, če jo vlijemo v drugo valjasto posodo, katere premer je 8-krat večji od premera prve? Odgovor izrazi v centimetrih.
odgovor: preveriti
V valjasti posodi nivo tekočine doseže 98 cm. Na kakšni višini bo nivo tekočine, če jo vlijemo v drugo valjasto posodo, katere premer je 7-krat večji od premera prve? Odgovor izrazi v centimetrih.
odgovor: preveriti
Khafrenova piramida ima obliko pravilne štirikotne piramide, katere stranica baze je 210 m, višina pa 144 m. Stranica baze tone muzejske kopije te piramide je 42 cm. Poiščite višino muzejski izvod. Odgovorite v centimetrih.
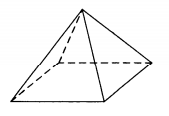
odgovor: preveriti
Piramida Menkaure ima obliko pravilne štirikotne piramide, katere stranica dna je 102 m, višina pa 66 m. Stran dna natančne muzejske kopije te piramide je 34 cm. Poiščite višina muzejske kopije. Odgovorite v centimetrih. 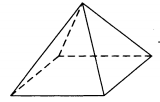
odgovor: preveriti
Bralcem "Habrahabra" ponujam prevod publikacije "100 Prisoners Escape Puzzle", ki sem jo našel na spletni strani DataGenetics. Vse napake v tem članku pošljite v zasebna sporočila.
Glede na pogoj problema je v zaporu 100 zapornikov, od katerih ima vsak svojo osebno številko od 1 do 100. Ječar se odloči, da bo zapornikom dal priložnost za izpustitev in jim ponudi, da opravijo test, ki si ga je izmislil. Če vsem ujetnikom uspe, potem so svobodni, če vsaj enemu ne uspe, vsi umrejo.
Naloga
Ječar gre v skrivno sobo in pripravi 100 škatel s pokrovi. Na vsako škatlo označi številke od 1 do 100. Nato prinese 100 papirnatih tablic, glede na število zapornikov, in te tablice oštevilči od 1 do 100. Nato premeša 100 tablic in v vsako škatlo položi eno tablico, zapiranje pokrova. Zaporniki ne vidijo, kako ječar izvaja vsa ta dejanja.Začne se tekmovanje, ječar vsakega zapornika enega za drugim odpelje v sobo s škatlami in zapornikom pove, da morajo najti škatlo, v kateri bo ploščica s številko zapornika. Zaporniki poskušajo najti ploščico s svojo številko tako, da odprejo škatle. Vsak lahko odpre do 50 škatel; če vsak od zapornikov najde svojo številko, bodo zaporniki izpuščeni, če vsaj eden od njih ne najde svoje številke v 50 poskusih, bodo vsi zaporniki umrli.

Da bi bili zaporniki izpuščeni, morajo VSI zaporniki uspešno prestati test.
Kakšna je torej možnost, da bodo zaporniki pomiloščeni?
- Ko zapornik odpre škatlo in preveri ploščo, jo položi nazaj v škatlo in pokrov ponovno zapre;
- Mesta plošč ni mogoče spremeniti;
- Zaporniki drug drugemu ne morejo puščati namigov ali kakor koli komunicirati drug z drugim, ko se sojenje začne;
- Zaporniki lahko razpravljajo o strategiji pred začetkom sojenja.
Kakšna je optimalna strategija za zapornike?
Dodatno vprašanje:
Če bo prijatelj zapornikov (ki ni udeleženec testa) lahko vstopil v skrivno sobo pred začetkom testa, preglejte vse tablete v vseh škatlah in (po želji, vendar ni obvezno) zamenjajte dve tableti iz dveh škatel (v tem primeru tovariš ne bo imel možnosti obvestiti ujetnikov o rezultatu svojih dejanj), kakšno strategijo naj potem sprejme, da poveča možnosti ujetnikov za pobeg?
Rešitev neverjetna?
Na prvi pogled se zdi ta naloga skoraj brezupna. Zdi se, da je možnost, da bi vsak od zapornikov našel svojo tablico, mikroskopsko majhna. Poleg tega zaporniki med sojenjem ne morejo izmenjevati informacij med seboj.Možnosti enega zapornika so 50:50. Skupaj je 100 škatel in lahko odpre do 50 škatel in išče svoj znak. Če naključno odpre škatle in odpre polovico vseh škatel, bo svojo tablico našel v odprti polovici škatel ali pa bo njegova tablica ostala v zaprtih 50 škatlah. Njegove možnosti za uspeh so ½.

Vzemimo dva ujetnika. Če oba naključno izbereta polja, bodo možnosti za vsakega od njiju ½, za dva pa ½x½=¼.
(pri dveh zapornikih bo uspeh v enem primeru od štirih).
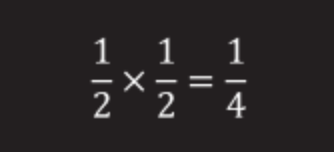
Za tri zapornike je kvota ½ × ½ × ½ = ⅛.
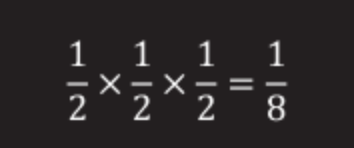
Za 100 zapornikov so kvote: ½ × ½ × … ½ × ½ (pomnožite 100-krat).

To je enako Pr ≈ 0,00000000000000000000000000000008
Torej je zelo majhna možnost. V tem scenariju bodo najverjetneje vsi zaporniki mrtvi.
Neverjeten odgovor
Če vsak zapornik naključno odpre škatle, je malo verjetno, da bo opravil test. Obstaja strategija, pri kateri lahko zaporniki pričakujejo, da bodo uspešni več kot 30 % časa. To je osupljivo neverjeten rezultat (če za to matematično težavo še niste slišali).Več kot 30% za vseh 100 zapornikov! Da, to je celo več kot možnosti za dva zapornika, pod pogojem, da naključno odpirata škatle. Toda kako je to mogoče?
Jasno je, da ena za vsakega zapornika, možnosti ne morejo biti višje od 50% (navsezadnje ni možnosti za komunikacijo med zaporniki). Vendar ne pozabite, da so informacije shranjene na lokaciji tablic znotraj škatel. Nihče ne meša tablic med obiski sobe posameznih zapornikov, zato lahko te informacije uporabimo.
rešitev
Najprej vam bom povedal rešitev, nato pa razložil, zakaj deluje.Strategija je izjemno enostavna. Prvi od ujetnikov odpre škatlo s številko, ki je napisana na njegovih oblačilih. Na primer, zapornik številka 78 odpre škatlo s številko 78. Če najde svojo številko na ploščici znotraj škatle, je to super! Če ne, pogleda številko na krožniku v "svoji" škatli in nato odpre naslednjo škatlo s to številko. Ko odpre drugo škatlo, pogleda številko tablice v tej škatli in odpre tretjo škatlo s to številko. Nato to strategijo preprosto prenesemo v preostale škatle. Za jasnost si oglejte sliko:
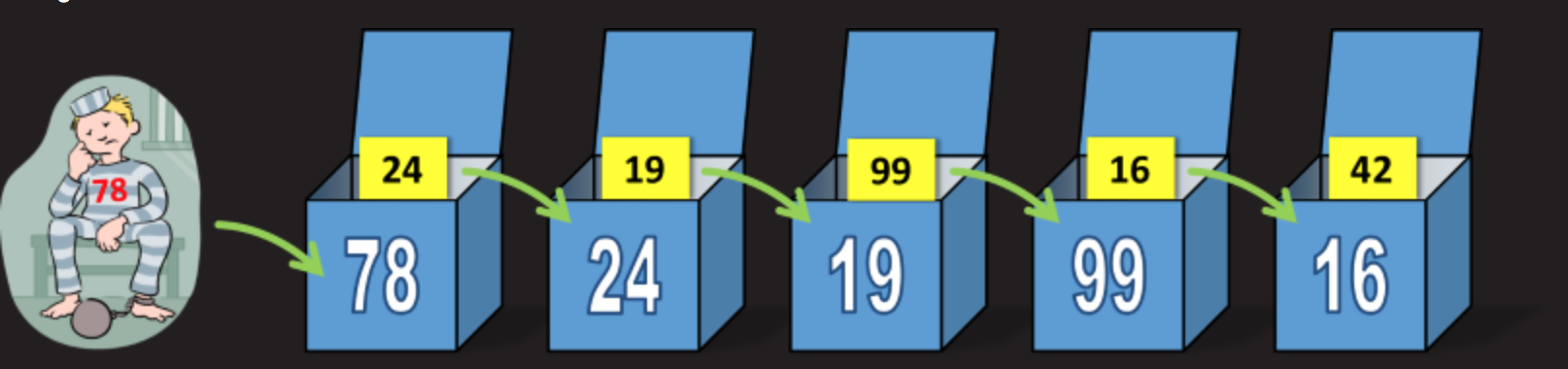
Sčasoma bo zapornik bodisi našel svojo številko bodisi dosegel omejitev 50 škatlic. Na prvi pogled je to videti nesmiselno v primerjavi z preprosta izbiraškatle naključno (in za enega posameznega zapornika, to drži), a ker bo vseh 100 zapornikov uporabljalo isti niz škatel, je to smiselno.
Lepota tega matematičnega problema ni samo vedeti rezultat, ampak tudi razumeti zakaj ta strategija deluje.
Zakaj torej strategija deluje?
Vsaka škatla vsebuje en krožnik – in ta krožnik je unikaten. To pomeni, da je plošča v polju z isto številko ali kaže na drugo polje. Ker so vse plošče edinstvene, obstaja samo ena plošča za vsako škatlo, ki kaže nanjo (in samo en način, kako priti do te škatle).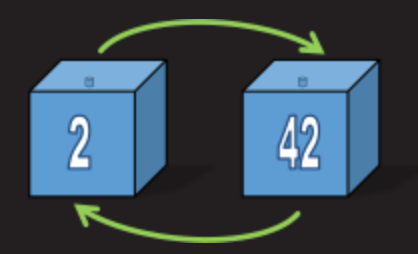
Če dobro pomislite, škatle tvorijo zaprto krožno verigo. Ena škatla je lahko del samo ene verige, saj je znotraj škatle samo en kazalec na naslednjo in zato je v prejšnjem polju samo en kazalec na to škatlo (programerji lahko vidijo analogijo s povezanimi seznami).
Če polje ne kaže nase (številka polja je enaka številki tablice v njem), bo v verigi. Nekatere verige so lahko sestavljene iz dveh polj, nekatere so daljše.
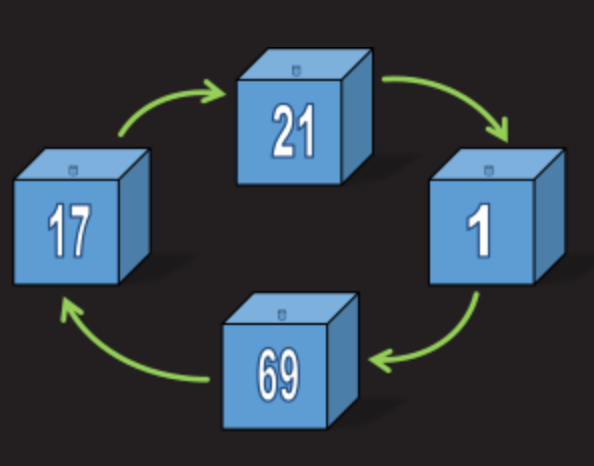
Ker vsi zaporniki začnejo s škatlo z isto številko na svojih oblačilih, so po definiciji postavljeni na verigo, ki vsebuje njihovo imensko tablico (na to škatlo je samo ena ploščica z imenom).
Z raziskovanjem polj vzdolž te verige v krogu je zagotovljeno, da bodo na koncu našli svoj znak.
Vprašanje ostaja le, ali bodo svojo tablico našli v 50 potezah.
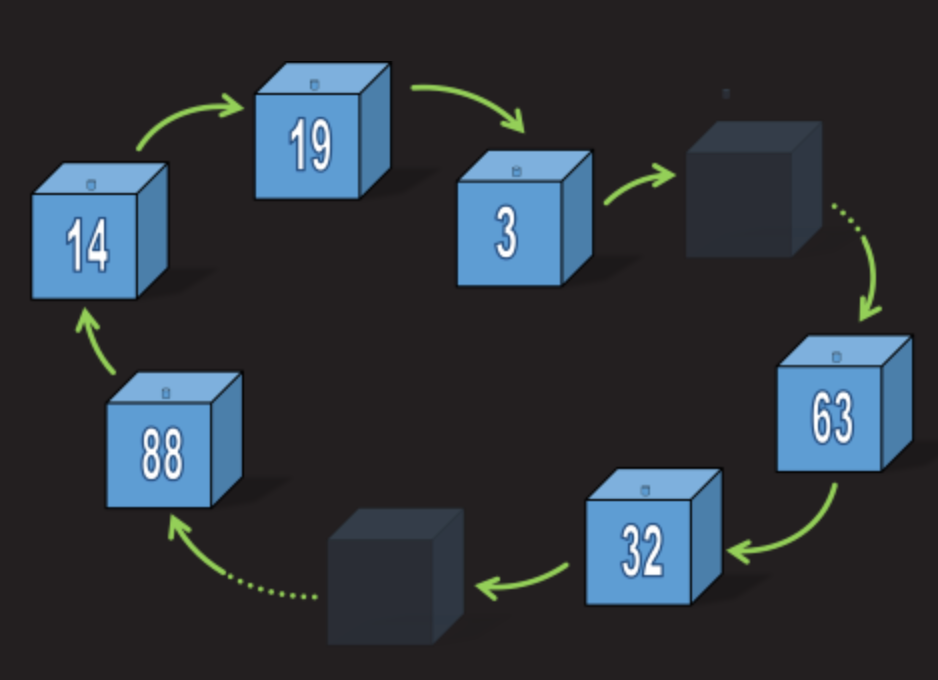
Dolžina verige
Da bi vsi zaporniki opravili test, mora biti največja dolžina verige manjša od 50 škatel. Če je veriga daljša od 50 škatel, bodo zaporniki s številkami iz teh verig padli na preizkusu - in vsi zaporniki bodo mrtvi.Če je največja dolžina najdaljše verige manjša od 50 škatel, bodo test opravili vsi zaporniki!
Za trenutek pomislite. Izkazalo se je, da je lahko samo ena veriga, ki je daljša od 50 škatel v kateri koli postavitvi plošč (imamo samo 100 škatel, tako da če je ena veriga daljša od 50, potem bodo preostale skupaj krajše od 50).
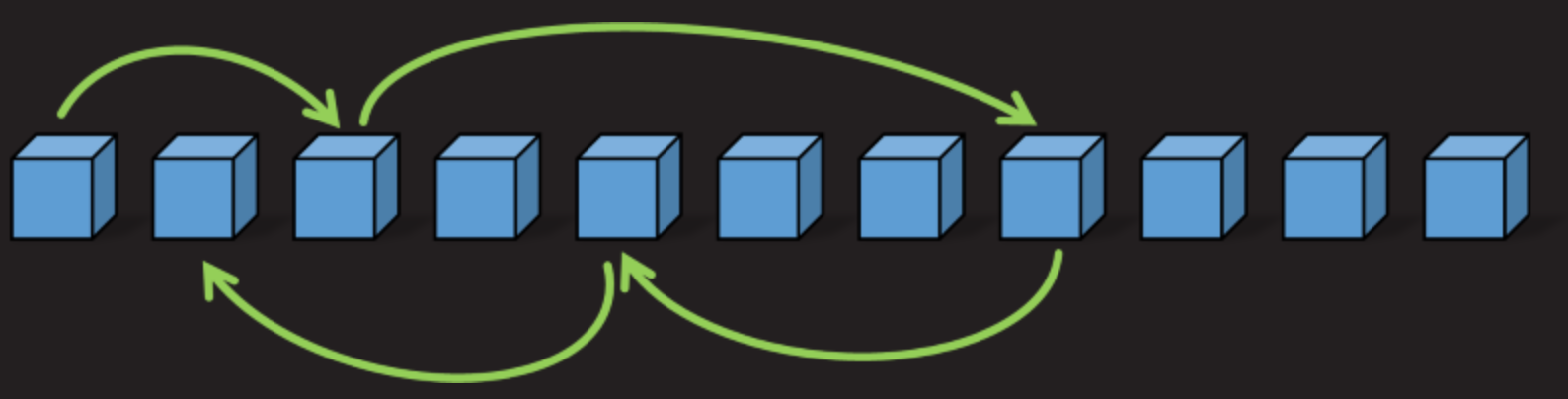
Kvote z dolgo verigo
Ko ste se prepričali, da mora biti največja dolžina verige manjša ali enaka 50 za uspeh in da je lahko v katerem koli nizu samo ena dolga veriga, lahko izračunamo verjetnost, da boste opravili izziv:Še nekaj matematike
Kaj torej potrebujemo, da ugotovimo verjetnost dolge verige?Za verigo dolžine l je verjetnost, da bodo polja izven te verige:
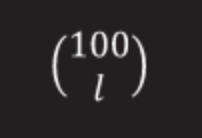
V tej zbirki številk je (l-1)! načine za razporeditev znakov.
Preostale znake je mogoče locirati (100-l)! načine (ne pozabite, da dolžina verige ne presega 50).
Glede na to je število permutacij, ki vsebujejo niz natančne dolžine l: (>50)

Izkazalo se je, da obstaja 100(!) načinov za razporeditev plošč, tako da je verjetnost obstoja verige dolžine l enaka 1/l. Mimogrede, ta rezultat ni odvisen od števila škatel.
Kot že vemo, lahko obstaja le en primer, v katerem obstaja veriga z dolžino > 50, zato se verjetnost uspeha izračuna po tej formuli:
Rezultat
31,18% - verjetnost, da bo velikost najdaljše verige manjša od 50 in bo vsak od zapornikov lahko našel svojo tablico glede na omejitev 50 poskusov.Verjetnost, da bodo vsi zaporniki našli svoje tablice in opravili test, je 31,18 %.
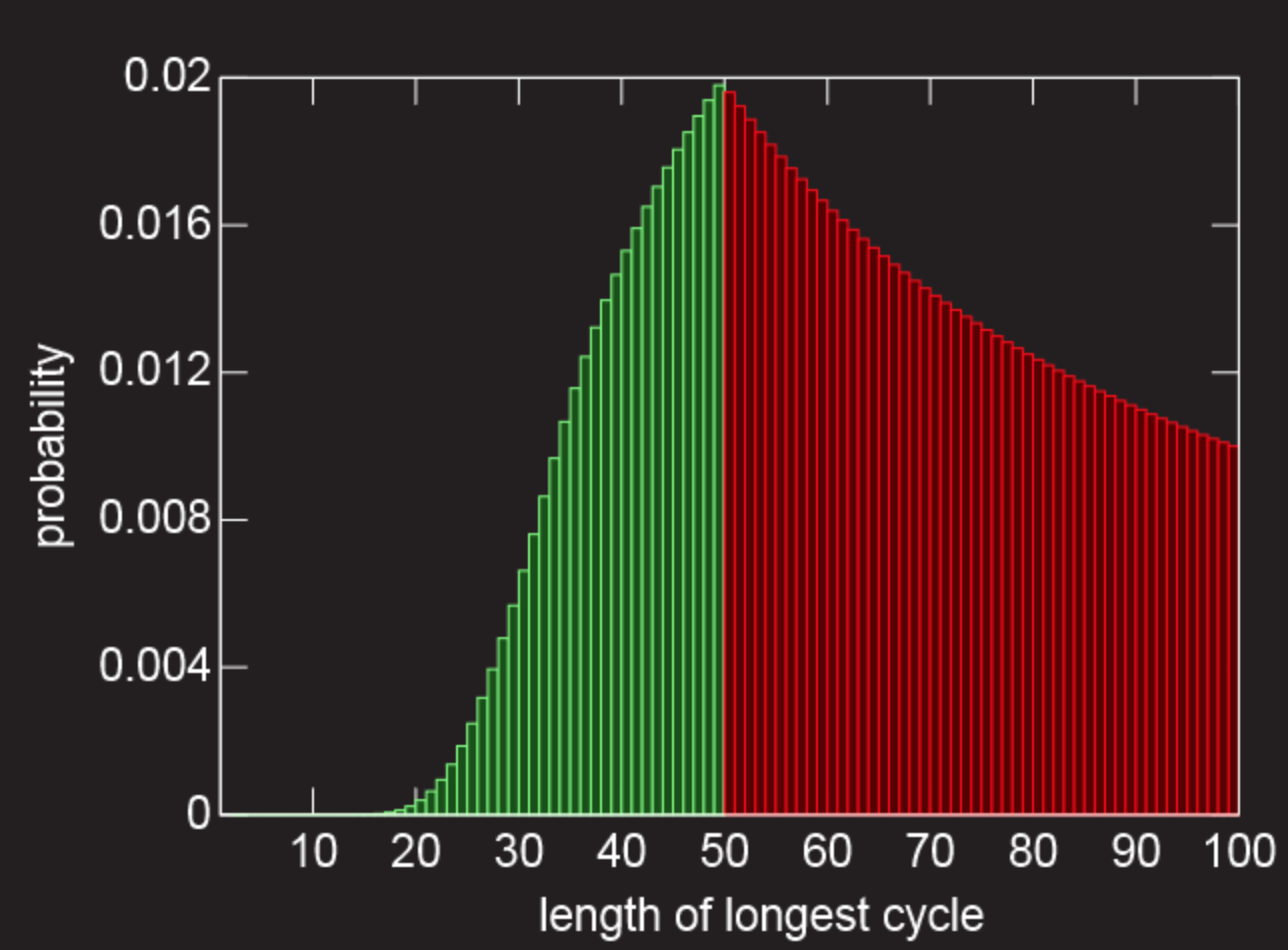
Spodaj je graf, ki prikazuje verjetnosti (na y-osi) za vse verige dolžine l (na x-osi). Rdeča pomeni vse "napake" (navedena krivulja je le graf 1/l). Zelena pomeni "uspeh" (izračun je za ta del grafa nekoliko bolj zapleten, saj obstaja več načinov za določitev največje dolžine<50). Общая вероятность складывается из зеленых столбцов в 31.18% шанс на спасение.
Harmonično število (ta del članka je za geeke)
V matematiki je n-to harmonično število vsota recipročnih vrednosti prvih n zaporednih števil naravnega niza.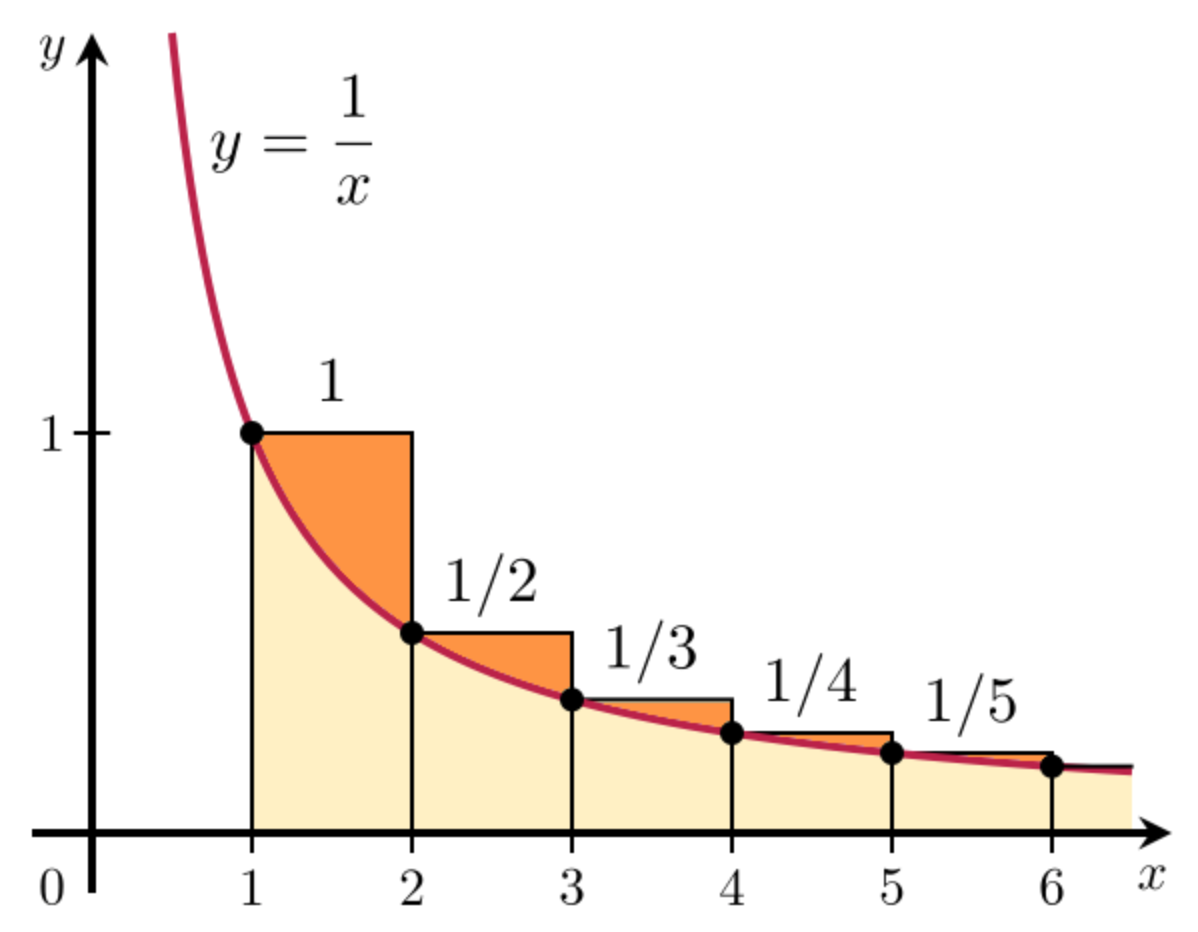
Izračunajmo limit, če imamo namesto 100a škatel poljubno veliko število škatel (predpostavimo, da imamo skupaj 2n škatel).
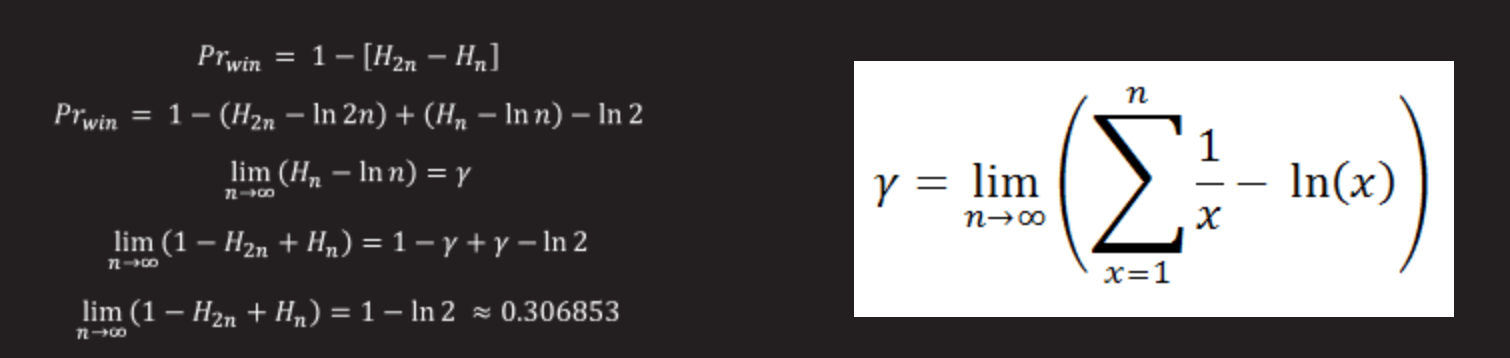
Euler-Mascheronijeva konstanta je konstanta, definirana kot meja razlike med delno vsoto harmoničnega niza in naravnim logaritmom števila.
Ko se število zapornikov poveča, če nadzornik dovoli zapornikom, da odprejo polovico vseh škatel, se možnost rešitve nagiba k 30,685 %.
(Če ste se odločili, da zaporniki naključno ugibajo škatle, se z naraščanjem števila zapornikov verjetnost, da boste rešeni, nagiba k ničli!)
Dodatno vprašanje
Se še kdo spomni dodatnega vprašanja? Kaj lahko stori naš ustrežljivi tovariš, da poveča naše možnosti za preživetje?Zdaj že poznamo rešitev, zato je strategija preprosta: pregledati mora vse znake in najti najdaljšo verigo škatel. Če je najdaljša veriga manjša od 50, mu tablet sploh ni treba menjati oziroma jih zamenjati tako, da najdaljša veriga ne postane daljša od 50. Če pa najde verigo, daljšo od 50 škatel, mora le zamenjati vsebino dveh škatel iz te verige, da to verigo razdeli na dve krajši verigi.
Zaradi te strategije ne bo dolgih verig in vsi zaporniki bodo zagotovo našli svoje znamenje in odrešitev. Torej z zamenjavo dveh znamenj zmanjšamo verjetnost odrešitve na 100%!
DOMAČA NALOGA #21. semester, MOŽNOST - 1
1. Izračunajte po definiciji odvod funkcije Differential" href="/text/category/differentcial/" rel="bookmark"> diferencialna enačba l'' + Al' + Bl = 0 .
a(ex + x) + x3 - 1 = 0 z majhnim parametrom a .
x = Cosx .
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA"> DOMAČA NALOGA št. 2
1. semester, MOŽNOST - 3
1..gif" width="357" height="45">.
5. Z linearizacijo reši enačbo a(2x +lnx) + x3 - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe = Cosx .
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 4
1..gif" width="120" height="24 src="> .
AMPAK in AT funkcijo l= (Ax + B) e–x l’’ + 2 l’ + 3 l= (4x + 6) e–x.
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x4 + x) + x3 - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe lnx = Cosx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 5
1..gif" width="137" height="24 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l= e2x Cos3 x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo ahttp://pandia.ru/text/78/495/images/image019_30.gif" width="103" height="24 src="> na segmentu [ 0,9 ; 4].
8. Določite mere krožnega stožca tako, da za dano prostornino V imela je minimalno stransko površino.
1. semester, MOŽNOST - 6
1..gif" width="139" height="24 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (3 x+ 1) e–3x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
Pridobite celotno besedilo4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x2 +lnx) + x3 - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe e– x = lnx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 7
1..gif" width="144" height="24 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = kot v2 x + Bcos2 x je rešitev diferencialne enačbe l’’ + 3 l’ – 4 l = –14 greh2 x – 2 Cos2 x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(ex + x) + lnx = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe x = e– x . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA"> DOMAČA NALOGA št. 2
1. semester, MOŽNOST - 9
1..gif" width="383" height="55">.
5. Z linearizacijo reši enačbo a(2 x+ x3) + lnx = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe = e– x . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA"> DOMAČA NALOGA št. 2
1. semester, MOŽNOST - 11
1..gif" width="389" height="45">.
5. Z linearizacijo reši enačbo a/text/categ/nauka.php" class="myButtonNauka">Pridobi celotno besedilo
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 12
1..gif" width="148" height="24 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (sekira + B) e– x je rešitev diferencialne enačbe l’’– 2 l’ + 3 l = (12 x + 10) e– x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(3 x2 + x) + lnx = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe x – 1 = sinx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 13
1..gif" width="127" height="24 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l= e–x Cos2 x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(ex + x) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe = sinx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 14
1..gif" width="153" height="24 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (3 x+ 2) e–x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(ex + x2) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe 1 – x = sinx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 15
1..gif" width="129" height="27 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = kot v2 x + Bcos2 x je rešitev diferencialne enačbe l’’ – 3 l’ – 4 l = – 2 greh2 x – 14 Cos2 x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x +lnx) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe x3 – 1 = sinx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 16
1..gif" width="136" height="27 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (sekira + B) e– x je rešitev diferencialne enačbe l’’ + 5 l’ + 3 l = –2 x e– x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x3 + x2) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe 1/| x| = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 17
1..gif" width="153" height="27 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l= e–2xgreh2 x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
Pridobite celotno besedilo4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(ex + x3) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe 1 – x = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 18
1..gif" width="87" height="39 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (3 – x) e2x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x2 +lnx) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 19
1..gif" width="92" height="41 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = kot v2 x + Bcos2 x je rešitev diferencialne enačbe l’’ + 2 l’ + 3 l = – 5 greh2 x + 3 Cos2 x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(ex + x) +ln(2 x – 1) = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe 2 – x = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1 semester, MOŽNOST - 20
1..gif" width="92" height="41 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (sekira + B) e–x je rešitev diferencialne enačbe l’’ + 5 l’ – 3 l = (– 14 x – 15) e– x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x5 + x) +ln(2 x – 1) = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe arctgx = – lnx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="81" height="44">
1. semester, MOŽNOST - 21
1..gif" width="92" height="39 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l= e–2x Cos2 x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(ex + 2x) +ln(2 x – 1) = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe npr = 2 – x . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="81" height="44"> se vrti okoli osi X. V nastali elipsoid je včrtan krožni valj. Določite mere tega valja tako, da bo imel največjo stransko površino.
1. semester, MOŽNOST - 22
1..gif" width="95" height="43 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (1 – 2 x) e3x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x3 + x4) +ln(2 x – 1) = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe npr = . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije /text/categ/nauka.php" class="myButtonNauka">Pridobi celotno besedilo
1. semester, MOŽNOST - 23
1..gif" width="125" height="39 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = kot v2 x + Bcos2 x je rešitev diferencialne enačbe l’’ + 2 l’ – 3 l = – 11 greh2 x – 3 Cos2 x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a + ln(2 x – 1) = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe npr = 1/ x . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, MOŽNOST - 24
1..gif" width="125" height="39 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (sekira + B) e– x je rešitev diferencialne enačbe l’’– 5 l’ – 3 l = (6 x – 5) e– x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(1 + 3x) +ln(2 x – 1) = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe npr = . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA"> DOMAČA NALOGA št. 2
1. semester, IZBIRA - 26
1..gif" width="396" height="55">.
5. Z linearizacijo reši enačbo a(ex + x) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe lnx = . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA"> DOMAČA NALOGA št. 2
1. semester, MOŽNOST - 28
1..gif" width="167" height="27 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (sekira + B) e– x je rešitev diferencialne enačbe l’’ – 5 l’ + 3 l = (18 x + 13) e– x .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x2 + x) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe lnx = 1/ x . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
Pridobite celotno besedilo7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1. semester, IZBIRA - 29
1..gif" width="167" height="27 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l= e3x Cos2 x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x +lnx) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe lnx = . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7. Poiščite natančno oceno funkcije 102" height="30" bgcolor="#EAEAEA" style="border:.75pt solid black; vertical-align:top;background:#EAEAEA">
1 semester, MOŽNOST - 30
1..gif" width="132" height="43 src="> . Narišite te črte in zahtevani kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l = (5 – x) e5x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(prej +lnx) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe lnx = 4 - x2. Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="81" height="44"> je skozi točko M(–3; 0) narisanih tetiv. Poišči največjo dolžino teh tetiv.
1. semester, IZBIRA - 31
1..gif" width="371" height="48">.
5. Z linearizacijo reši enačbo ahttp://pandia.ru/text/78/495/images/image027_23.gif" width="172" height="27 src="> na segmentu.
8. Iz žice dolžine L je izdelan okvir pravilne štirikotne prizme. Določite mere te prizme tako, da bo njena stranska površina največja.
1. semester, IZBIRA - 32
1..gif" width="148" height="24 src="> . Narišite te črte in želeni kot.
3. Ugotovite, pri katerih vrednostih AMPAK in AT funkcijo l= e–x Cos2 x je rešitev diferencialne enačbe l'' + Al' + Bl = 0 .
4. S pomočjo linearizacijske formule in ekvivalenčnih formul izračunajte meje
5. Z linearizacijo reši enačbo a(x +lnx) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe 1/| x| = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="77" height="39 src=">.
2..gif" width="403" height="52">.
5. Z linearizacijo reši enačbo a(ex + x) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe lnx = . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="72" height="39 src=">.
2..gif" width="375" height="44">.
5. Z linearizacijo reši enačbo a(ex + x) + lnx = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe e– x = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="72" height="39 src=">.
2..gif" width="399" height="49">.
5. Z linearizacijo reši enačbo a(ex + x3) + - 1 = 0 z majhnim parametrom a .
6. Grafično poiščite ničelni približek korena enačbe = arctgx . Nato izračunajte ta koren z Newtonovo metodo s petimi decimalnimi mesti.
7..gif" width="81" height="44"> se vrti okoli osi X. V nastali elipsoid je včrtan krožni valj. Določite mere tega valja, tako da bo imel največjo prostornino.



